雙陸棋
维基百科，自由的百科全书
| 双陆棋 | |
|---|---|
 双陆棋，由一个棋盘、三十枚棋子、四个骰子、一个倍数方块、以及两个装骰子的杯子组成 |
|
| 玩家數目 | 2 |
| 年齡 | 5岁以上 |
| 準備時間 | 10-30秒 |
| 遊戲時間 | 5-30分钟 |
| 複雜程度 | 中等 |
| 策略成份 | 甚高 |
| 運氣成份 | 骰子 |
| 所需技巧 | 计算、战术、策略、概率 |
雙陸棋（香港和澳门又称百家乐棋）是一種供两人对弈的棋盤遊戲，棋子的移动以掷骰子的点数决定，首位把所有棋子移离棋盘的玩者可获得胜利。游戏在世界多个地方演变出多个版本，但保留一些共通的基本元素。
在遊戲中，每位玩者盡力把棋子移動及移離棋盤。虽然游戏有很大的运气成分，遊戲的策略仍然十分重要。每次擲骰子时，玩者都要從多種選擇中選出最佳的走法。计算机科学家们对双陆棋做了很多研究，目前双陆棋软件已经可以击败世界级的人类选手。
目录 |
[编辑] 历史
中国古代的双陆棋是一种类似赌博的棋戏，相传是在由印度传入的波罗塞戏基础上，由曹魏时王子曹植糅合六博的特点而创设的，初期有两枚骰子，唐朝末年后逐渐加到六枚。双陆棋子为马形，黑白各十五枚，两人相博，掷骰子按点行棋。双陆棋在唐朝、五代和元朝曾风靡一时，连后唐明宗也喜欢下双陆棋。但明朝和清朝时，由于麻将和象棋的出现，使得下双陆棋的人数逐渐减少，最终导致双陆棋在清朝中叶时失传。
西方的雙陸棋起源於大约公元前3000年古埃及的一种游戏—Senet，[1]此外古罗马人也曾玩过一种类似双陆棋的游戏。[2]11世纪时，双陆棋传到法国，很快成为赌徒们最喜爱的游戏，以致于路易九世在1254年颁布了一项法令，禁止官员们下双陆棋。[3][4]12世纪时，双陆棋传到德国，13世纪时传到了冰岛。17世纪时还传到了瑞典，当时在瑞典的一艘沉船里发现了一个木制的双陆棋棋盘和一些棋子。[5]19世纪时，随着西方列强大量建立殖民地，双陆棋传遍了全世界。至今双陆棋仍風行於西方社會，這個遊戲適合兩人對奕，各自執一黑一白之十五個棋子，遊戲有一個固定的開始擺設方式，雙方各有一個杯子裝兩箇骰子，为求公平只能由手持杯子擲骰子，雙陸棋一般使用的棋具外觀優美，由於技巧與運氣因素各佔一半，因此適合酌彩。
在英语和绝大多数欧洲语言中，双陆棋一词为“backgammon”，“back”是“后退”的意思，而“gammon”在中古英语中则有“游戏”的意思。该词最早在1650年的牛津英语词典中出现。[6]
[编辑] 规则
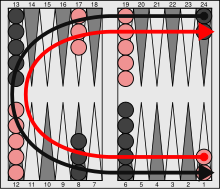
双陆棋的目的是将己方所有棋子越过对方，然后再移离棋盘。游戏开始时，棋子较为分散，在游戏过程中可能被对方攻击或阻挡。由于下一盘棋所需的时间很短，比赛中通常采用计分制，首先获得一定分数的一方为胜利者。
[编辑] 设备
- 棋盘
- 两套不同颜色的十五枚棋子(每位玩者一套)
- 四个骰子(每位玩者两个)
- 倍数方块
[编辑] 摆法
棋盘的每一条边上都有十二个三角形(如上图所示)，从右下角开始依顺时针方向用数字1到24编号（对方则正好相反，从右上角开始依逆时针方向编号，己方的第1点就是对方的第24点，己方的第2点就是对方的第23点，依此类推）。每位玩者将两枚棋子放在第24点，三枚棋子放在第8点，五枚棋子放在第13点，五枚棋子放在第6点。[7]
第1点到第6点叫做内盘或主盘，第7点到第12点叫做外盘。第7点又叫做临界点，第13点又叫做中点。[7][8]
[编辑] 走法
游戏开始时，双方各掷一个骰子，点数较大的一方先走。双方轮流移动棋子，每次移动前掷两个骰子。[7][8]
掷骰子后，玩者必须按照掷得的点数移动棋子。例如，如果掷到6和3，就必须将一枚棋子向前移动6个点，再将另一枚棋子向前移动3个点。也可以将同一枚棋子移动6个点再移动3个点，或先移动3个点再移动6个点，但不能直接移动9个点。如果掷到两个相同的点数，就要按照掷得的点数移动棋子两次。例如，如果掷到两个5，就要将四枚棋子向前移动5个点。[7][8]
[编辑] 攻击弱棋
棋子只能移动到未被占据或被己方棋子占据的点，也可以移动到仅被一枚对方棋子占据的点——对方的这枚棋子叫做弱棋。弱棋被攻击后放在棋盘中央的分界上。棋子不能移动到已被两枚或以上对方棋子占据的点。因此不可能有任何点同时被己方和对方的棋子占据。[7][8]
被攻击的棋子离开分界之前，其它棋子不得移动。如果掷到2，就可将分界上的棋子移动到第23点；如果掷到3，就可将分界上的棋子移动到第22点，依此类推。[7][8]
[编辑] 移离棋盘
如果所有棋子都回到了己方内盘，就可以开始将棋子移离棋盘。如果掷到1，就可将位于第1点的棋子移离棋盘；如果掷到2，就可将位于第2点的棋子移离棋盘，依此类推。不能将比所掷数字更低点的棋子移离棋盘，除非前面已经没有任何棋子。[7][8]例如，如果掷到5和4，第4点有两枚棋子，而第5点和第6点都没有棋子，才可以从第4点将两枚棋子移走；如果第5点没有棋子，但第6点仍有棋子，则不能移动两枚第4点的棋子。
如果在移离棋盘时有棋子被对方攻击，就必须等该棋子回到了己方内盘后才可以继续移离棋盘。
[编辑] 胜负与得分
首先将所有棋子移离的一方获得勝利，可得一分。如果玩者还未開始将棋子移离棋盘，而对方已将所有棋子移离，对方就获得两分，称为“全胜”或“家乐”。如果玩者还未開始将棋子移离棋盘，且仍有棋子在分界上或在对方内盘上，而对方已将所有棋子移离，对方就获得三分，称为“完胜”或“百家乐”。[7][8]
[编辑] 总点数
对局中某一方所有棋子所在的点数之和（分界上相当于第25点）叫做“总点数”。开局时双方的总点数为167（最高可达375）。对局过程中总点数一般逐渐减少，但当棋子被攻击而进入分界时，总点数增加。哪一方总点数小，就意味着哪一方领先。比赛时是不允许用计算器计算总点数的，因此双陆棋棋手们必须具有敏捷的心算能力。[9]
[编辑] 倍数方块
倍数方块（又称倍数骰子）最早在1926年为纽约的双陆棋棋手们使用，[10]以后逐渐为全世界所采用。其目的是为了增加游戏的速度和难度，以及使游戏更富有趣味性。倍数方块是刻上数字2、4、8、16、32和64的立方体。掷骰子之前，玩者可以要求将所得的分数加倍。对方必须立刻接受要求，或认输。如果接受要求，就将倍数方块转到数字2朝上，所得的分数将加倍。也就是说，获得胜利将得到两分，获得全胜将得到四分，而如果失败了，对方就获得两分。以后还可以加到更高的倍数。加倍的次数不限，可以加到128倍，256倍，但实际上很少加到4倍以上。[7][8]倍数方块要求玩者们不仅要选择最佳的着法，还需要估计取胜的概率。[10]
一般情况下，如果认为自己获胜的概率大于50%，应主动提出加倍要求；当对方提出加倍要求时，如果认为自己获胜的概率大于25%，就应该接受（这个概率不仅与双方的总点数以及棋子的位置有关，还与棋手个人的水平、风格以及看问题的角度有关）。但如果认为自己有机会获得全胜或完胜，就不要主动提出加倍要求，否则一旦对方认输，就只能得到一分。如果一时难以估计取胜的概率，不要主动提出加倍要求；但当对方提出加倍要求时，可以根据双方的总点数来判断是否应接受；如果己方的总点数比对方大10个点以上，就不应该接受加倍，否则应该接受加倍。
关于倍数方块还有两条很重要的规则：雅可比（Jacoby）规则和克罗福（Crawford）规则。雅可比规则规定，如果对局中未曾使用倍数方块，则获得全胜或完胜都只能得到一分。这条规则鼓励了棋手们使用倍数方块，而不是一直玩到底企盼着获得全胜或完胜。雅可比规则在赌博时广泛使用，但不在比赛中使用。[11]
克罗福规则规定，如果某一方只差一分就获得了比赛胜利，双方都不准使用倍数方块。使用这条规则的目的是防止某一方只差一分就获得比赛胜利时，对方为增加获胜的概率而提出加倍要求。克罗福规则经常在比赛中使用。[11]
[编辑] 对局记录
双陆棋的对局记录法由美国棋手Paul Magriel在20世纪70年代发明。[7]
掷骰子掷到4和2，记录为：4-2
从第8点移动一枚棋子到第4点，再从第6点移动一枚棋子到第4点，记录为：8/4 6/4[7][9]
攻击对方的弱棋，在着法后加星号（*）。例如，从第13点移动一枚棋子到第7点，并攻击对方的弱棋，记录为：13/7*
从第13点移动一枚棋子到第7点，并攻击对方的弱棋，再移动到第5点，记录为：13/7*/5[7][9]
移动超过一枚棋子，在着法后注明移动棋子的数目。例如，掷到两个2，从第6点移动三枚棋子到第4点，再从第13点移动一枚棋子到第11点，记录为：2-2 6/4(3) 13/11。[7][9]
用bar表示分界，off表示移离棋盘，例如bar/22 17/9，5/off 2/off。[7][9]
[编辑] 开局
双陆棋的开局要比其它棋盘游戏如中国象棋和国际象棋复杂，这是因为每次掷骰子都有21种可能的骰点组合，每一种组合又有多种可行的着法。以下只讨论第一步的最佳着法。
| 骰点 | 最佳着法 | 其它可行的着法 | ||
|---|---|---|---|---|
| 2-1 | — | 13/11, 6/5 | 13/11, 24/23 | — |
| 3-1 | 8/5, 6/5 | — | — | — |
| 4-1 | 13/9, 24/23 | 13/8 | — | — |
| 5-1 | 13/8, 24/23 | 13/8, 6/5 | — | — |
| 6-1 | 13/7, 8/7 | — | — | — |
| 3-2 | 13/11, 24/21 | 13/10, 13/11 | — | — |
| 4-2 | 8/4, 6/4 | — | — | — |
| 5-2 | 13/8, 24/22 | 13/8, 13/11 | — | — |
| 6-2 | 13/11, 24/18 | — | — | — |
| 4-3 | — | 13/10, 13/9 | 13/10, 24/20 | 13/9, 24/21 |
| 5-3 | 8/3, 6/3 | — | — | — |
| 6-3 | 24/18, 13/10 | 24/15 | — | — |
| 5-4 | 13/8, 24/20 | 13/8, 13/9 | — | — |
| 6-4 | — | 8/2, 6/2 | 24/14 | 24/18, 13/9 |
| 6-5 | 24/13 | — | — | — |
这里有几条规律，如果能够占据某个点，应尽可能占据，例如掷到6和1可以占据第7点。这样一方面可以起到阻挡对方的作用，另一方面第7点就可以作为根据地，以后可以放上更多棋子。
如果不能够占据某个点，一般最佳开步为移动第24点及第13点的棋子，例如掷到3和4时，应走13/10，24/20 。移动到第10点的棋子，虽然是一枚弱棋，但对方只有掷到相加为9的骰点（即6和3，或5和4）时才有机会攻击，概率只有九分之一；而且这枚棋子还增加了能够占据己方内盘某个点的概率，例如原来只有掷到4和2才能占据第4点，以后掷到6和2也可以了（10/4，6/4），为进一步阻挡对方棋子做好了准备。至于移动到第20点的棋子，虽然也是一枚弱棋，且很容易被对方攻击（对方掷到3或1就可攻击），但倘若对方真的攻击了，对方自己就要在第20点留下一枚弱棋，下一步掷到5或4时，就可以反攻；而且这枚棋子还能够防止对方从第12点移动棋子（例如，如果对方走12/16，下一步掷到4就可以走20/16攻击它），使对方难以占据外盘和内盘的点。另外还须注意，移动位于第13点的棋子时，移动的步数越小越好（除非能够移动到第8点），这样将尽可能减少被对方攻击的概率。
以上最佳开步乃是计算机分析的结果。一些过去曾认为最佳的开步，现在已被更好的着法取代。例如，过去曾认为掷到2和5时，最佳着法为13/11 13/8，但计算机分析结果表明，24/22 13/8的着法更好。
[编辑] 变体
双陆棋有不少变体，有的变体摆法有所改变，有的则是走法不同，还有的变体对某些骰子点数有特殊的规定。
一种常见的变体是任何一个点上最多允许有五枚棋子。虽然这不是官方的规则之一，但是在某些地区十分流行。[12]
Acey-deucey是一种双陆棋变体，开始时棋盘上没有棋子，必须在游戏时放入。如果掷到1和2，可以任意走动两枚棋子，如果掷到两个相同的点数，移动棋子后可再掷一次。
超级双陆〔Hypergammon〕是一种双陆棋变体，每位玩者只有三枚棋子，位于第24、23和22点上，该游戏已彻底解决，就是说，对于所有的三千二百万种局面，都已找到了取胜概率和最佳着法。[13][14]由于每位玩者只有三枚棋子，因此超级双陆的运气成分非常大，而策略成分则较小。
纳克双陆〔Nackgammon〕是一种双陆棋变体，由纳克·巴拉德（Nack Ballard）发明，摆法与双陆棋略有不同，第6点和第13点比双陆棋少放一枚棋子，第23点放两枚棋子。与双陆棋相比，纳克双陆开局时总点数较大（为195），因此所需时间较长，难度亦较大。[14][15]
日本双陆〔すごろく，Sugoroku〕是一种双陆棋变体，6世纪时由中国传入日本，现流行于日本。其摆法与双陆棋相同，但规则略有不同。主要区别为日本双陆中首先将所有棋子移入己方内盘即算胜利，无需再移离棋盘（因此也就无所谓全胜和完胜），因此所需时间较短。另外，日本双陆不使用倍数方块，也不允许占据连续六个点（所谓“占据某个点”是指该点至少有两枚己方的棋子）。与双陆棋相比，日本双陆规则比较简单。
[编辑] 策略与战术
最直接的策略就是避免被对方攻击或阻挡。要尽可能避免留下弱棋，如果一定要留下弱棋，要尽可能使受到攻击的概率为最小。一般情况下，当弱棋与对方棋子相距六个点时，最容易遭到对方攻击；无论是近一点还是远一点，受到攻击的概率都会减少。以下的表格给出了弱棋与对方棋子之间的距离，以及受到攻击的概率。
| 弱棋与对方棋子之间的距离 | 受到攻击的概率 |
|---|---|
| 1 | 30.6 % |
| 2 | 33.3 % |
| 3 | 38.9 % |
| 4 | 41.7 % |
| 5 | 41.7 % |
| 6 | 47.2 % |
| 7 | 16.7 % |
| 8 | 16.7 % |
| 9 | 13.9 % |
| 10 | 8.3 % |
| 11 | 5.6 % |
| 12 | 8.3 % |
| 15 | 2.8 % |
| 16 | 2.8 % |
| 18 | 2.8 % |
| 20 | 2.8 % |
| 24 | 2.8 % |
如果己方总点数大大领先于对方，应迅速将棋子越过对方，并移离棋盘。这种策略叫做“赛跑策略”。[9]如果己方总点数与对方相差不大，应采用“占有性策略”，就是用两枚棋子占据对方内盘某个点，这样以后就有机会攻击对方弱棋，或者掷到两个大骰点时就有机会逃脱。[9]
将连续六个点占据，使对方的棋子无法越过，这种策略叫做“阻挡策略”。[9]
将己方内盘上六个点全部占据，使对方被攻击的的棋子无法重新进入游戏，这样就可迅速取得优势，并获得胜利。这种策略叫做“闪电战策略”，是阻挡策略的一个特例。[7]
如果己方总点数落后于对方，可以保留一些棋子在对方内盘上，并在己方内盘上建立屏障，等对方棋子回到内盘时，就有机会攻击它们。这种策略叫做“撤退策略”。撤退策略并不是一个十分有效的策略，使用撤退策略的棋局中只有20%能够获得胜利。撤退策略只适用于己方总点数已大大落后于对方的情形，如果一开始就使用撤退策略，那么通常都会失败。[7][9]
将所有弱棋保持在与对方棋子相同的距离上。例如，将所有弱棋放在对方必须掷到2才能攻击到的点上。这样将减少被对方攻击的概率。[7][9]还有一种很重要的策略，有时无法直接攻击对方弱棋或占据某个点，这时就要考虑到下一步，使得下一步能够有最大的机会攻击对方弱棋或占据某个点。这种策略叫做“多样化策略”。[9]
[编辑] 国际比赛
世界双陆棋锦标赛始于1979年，在摩纳哥蒙特卡洛举行，比赛持续一个星期，每年都吸引了数千名选手和旁观者。[16]
[编辑] 软件
20世纪70年代，一名德国棋手Hans Berliner编写了双陆棋程序BKG 9.8。开始时，该程序跟初学者下棋也经常输；但后来Berliner使用了模糊逻辑的原理，使程序不断改进，最终在1979年7月以7:1击败了当时的世界冠军──意大利棋手Luigi Villa。Berliner指出，这多半是运气的原因，掷得的骰点对计算机比较有利。[17]
20世纪80年代晚期，程序员们使用一种叫人工神经网络的新方法，使双陆棋软件的水平大大提高。其中一种叫TD-Gammon的程序，由Gerald Tesauro编写，是第一个接近专家级水平的双陆棋程序。[18]美国棋手Bill Robertie和Kit Woolsey表示，TD-Gammon的水平已经高于世界上最好的棋手了。[18]
[编辑] 棋手
[编辑] 美洲棋手
- John Perkins Cushing （美国棋手）
- Billy Eisenberg （美国棋手，曾获1975年世界双陆棋锦标赛冠军）
- Robert Floyd （美国棋手）
- Dan Harrington （美国棋手）
- Oswald Jacoby （美国棋手，曾获1972年世界双陆棋锦标赛冠军）
- Joe Russell （美国棋手，曾获1989年世界双陆棋锦标赛冠军）
- Jason Lester （美国棋手）
- Paul Magriel （美国棋手，曾获1978年世界双陆棋锦标赛冠军）
- Bill Robertie （美国棋手，曾获1983年和1987年世界双陆棋锦标赛冠军）
- Alan Rosenberg （美国棋手）
- Erik Seidel （美国棋手）
- Kit Woolsey （美国棋手）
- Brian Zembic （加拿大棋手）
[编辑] 欧洲棋手
- Terence Reese （英国棋手）
- Charalambos Xanthos （英国棋手）
- Mads Andersen （丹麦棋手，曾获2002年世界双陆棋锦标赛冠军）
- Gus Hansen （丹麦棋手）
- Philip Vischjager （荷兰棋手，曾获2006年世界双陆棋锦标赛冠军）
- Luigi Villa （意大利棋手，曾获1979年世界双陆棋锦标赛冠军）
[编辑] 中东棋手
- Ezer Weizman （以色列棋手）
- Tunç Hamarat （土耳其棋手）
[编辑] 中国棋手
目前尚未有任何著名的中国双陆棋棋手。
[编辑] 参见
[编辑] 参考文献
- ^ Hayes, William C.（1946年3月.）． “"Egyptian Tomb Reliefs of the Old Kingdom"”．The Metropolitan Museum of Art Bulletin．New Series 4（7）：第170至178页．
- ^ Austin, Roland G.（1934年10月）． “Roman Board Games. I”．Greece & Rome．4（10）：第24至34页．
- ^ Murray, Harold James Ruthven（1952年）．“第六章: Race-Games”，A History of Board-Games Other than Chess．Hacker Art Books．ISBN 0-87817-211-4．
- ^ Lillich, Meredith Parsons（1983年3月）． “The Tric-Trac Window of Le Mans”．The Art Bulletin．65（1）：第23至33页．
- ^ Vasamuseet — The Swedish-Tables Association．The Vasa Museum．於2006年8月12日查閱．
- ^ （1989年）．“"backgammon"”．Oxford English Dictionary（牛津英语词典），第二版．于2006年8月5日访问．
- ^ 7.00 7.01 7.02 7.03 7.04 7.05 7.06 7.07 7.08 7.09 7.10 7.11 7.12 7.13 7.14 7.15 7.16 Robertie, Bill（2002年）．Backgammon for Winners，第三版，Cardoza．ISBN 1-58042-043-5．
- ^ 8.0 8.1 8.2 8.3 8.4 8.5 8.6 8.7 （2001年）Hoyle's Rules of Games，Third Revised and Updated Edition，Signet，第321至330页．ISBN 0-451-20484-0．
- ^ 9.00 9.01 9.02 9.03 9.04 9.05 9.06 9.07 9.08 9.09 9.10 Magriel, Paul（1976年）．Backgammon．Quadrangle/The New York Times Book Co.，第16至18页．ISBN 0-8129-0615-2．
- ^ 10.0 10.1 Robertie, Bill（2002年）．501 Essential Backgammon Problems，第二版，Cardoza，第22页．ISBN 1-58042-019-2．
- ^ 11.0 11.1 Robertie, Bill（2006年）．Backgammon for Serious Players，第二版，Cardoza，第19至22页．ISBN 0-940685-68-X．
- ^ bkgm.com上有相关讨论
- ^ Tesauro, G.（2002年）．“Programming backgammon using self-teaching neural nets”．Artificial Intelligence．134（1）：第181至199页．于2007年8月8日访问．
- ^ 14.0 14.1 Strato, Michael．Backgammon Variants．Gammonlife．於2007年8月8日查閱．
- ^ Woolsey, Kit（2001年9月）．Nackgammon．Gammonline．於2007年8月8日查閱．
- ^ Michael Crane（2000年7月25日）．Backgammon News — Wold Championships 2000．Mind Sports Worldwide．於2006年9月14日查閱．
- ^ Berliner, Hans，et al.（1980年1月）． “Backgammon program beats world champ”．ACM SIGART Bulletin（69）：第6至9页．
- ^ 18.0 18.1 Tesauro, Gerald（1995年3月）．“Temporal difference learning and TD-Gammon”．Communications of the ACM．38（3）：第58至68页．
[编辑] 外部連結
