拉姆齊定理
在組合數學上,拉姆齊定理(英語:Ramsey's theorem),又稱拉姆齊二染色定理,斷言對任意正整數和,若一個聚會的人數足夠大,則無論相識關係如何,必定有個人相識或個人互不相識。給定時,保證前述結論的最小值稱為拉姆齊數,其值取決於。用圖論術語複述:若將足夠大的完全圖各邊染紅藍兩色,則不論如何染,必定有紅色的階完全圖或藍色的階完全圖。[註 1]
拉姆齊定理是組合數學的重要結論,以弗蘭克·普倫普頓·拉姆齊命名。他在1930年論文《論形式邏輯的一個問題》[1]證明此定理最初的版本,開創現稱拉姆齊理論的組合理論分支。拉姆齊理論的主題是從「無序」尋找「規律」,希望找出某數學結構中,存在規律子結構的一般條件。在拉姆齊定理的圖論表述中,此「規律子結構」是同色集(monochromatic set),即頂點集的子集,其中各邊皆染成同一顏色。
拉姆齊定理不止一條,前述版本的若干引伸仍稱拉姆齊定理。例如,可以將二染色推廣至更多種色,此時定理斷言:對任意色數,和任意正整數,必有某數,使階的完全圖各邊不論如何染色,仍必可找到某(介於至)和某階完全子圖,其各邊皆染第色。可見拉姆齊二染色定理是的特例(同時取)。
例
[編輯]R (3, 3) = 6
[編輯]
在6個頂點的完全圖內,每邊塗上紅或藍色。欲證必然有一個紅色的三角形或藍色的三角形。
- 任意選取一個端點,它有5條邊和其他端點相連。
- 根據鴿巢原理,5條邊染兩種顏色,至少有3邊顏色相同,不失一般性設這種顏色是紅色,又設該三邊為。
- 三個頂點,互相連結的邊有三條。
- 若這3條邊中任何一條是紅色,這條邊的兩個端點和便組成一個紅色三角形。
- 若這3條邊中沒有紅邊,則都是藍色,因此,是藍色三角形。
以上論證對一切染色法都適用,所以的任何二染色皆有同色,換言之。這個定理的通俗版本稱為朋友與陌路人定理。
另一種證法是算兩次:考慮「異色角」的數目,即滿足為紅而為藍的有序三頂點組的個數。若先固定中間的頂點,則對應三元組的數目可能是
- (若其全部邊染同色);
- (若有四邊染某色,另一邊不同色);或
- (若有三邊染某色,另兩邊染另一色)。
所以,至多是,而本身有6種可能,異色角的總數至多是。但是,對於三邊不完全同色的三角形,恰好有兩隻異色角,所以,至多有個異色三角形。考慮到6個頂點組成個三角形,至少有兩個是同色三角形,再次得到的結論。
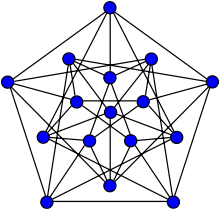
反之,將二染色,不一定有同色的三角形。此構造在同構意義下唯一,如下圖所示:將五個頂點排成一圈,每個端點和毗鄰的兩個端點之間的連線染紅色,與其餘兩個端點的連線染藍色,則不產生同色三角形。所以,。

1953年普特南數學競賽考過。[2]1947年匈牙利屈爾沙克·約瑟夫數學比賽(匈牙利語:Kürschák József Matematikai Tanulóverseny)亦然。[3]
R (3, 3, 3) = 17
[編輯]- 僅有兩種方法將16個頂點之間的邊染三種顏色而無同色三角形
-
無扭的
-
有扭的
多色拉姆齊數就是用三種或更多顏色的拉姆齊數。若不考慮對稱的情況,僅有兩個非平凡的多色拉姆齊數為已知:和。[4]
設將某完全圖的邊染紅綠藍三色,而無同色三角形。選任一頂點,考慮以紅邊與相連的各點,組成的「紅鄰域」。紅鄰域之內不能再有任何紅邊,否則該紅邊與一同組成紅色三角形。所以紅鄰域內的邊衹用藍綠兩色。由上節,的紅鄰域最多衹有5個頂點,否則有藍或綠的同色三角形。同理,的綠鄰域和藍鄰域,各有至多5個頂點,但圖中每個頂點,或為本身,或屬的某色鄰域,所以全圖至多個頂點。故。
欲證,現需用三種顏色畫出16個頂點的完全圖,而不產生同色三角形。若不辨同構之異,則恰有兩種畫法,分別稱為「無扭」(untwisted)和「有扭」(twisted)染法,見上圖。
的有扭或無扭染色中,選任一顏色,該色邊組成的子圖都是克萊布殊圖。
對較少頂點的完全圖,已知亦衹得兩種染三色的方法無同色三角形,分別來自的兩種染法,刪去任意一個頂點。則有115種方法染三色而無同色三角形,但此數不僅不辨圖同構(頂點的置換),還不辨顏色的置換。
拉姆齊數
[編輯]定義
[編輯]拉姆齊數,用圖論的語言有兩種描述:
- 對於所有的N頂圖,包含k個頂的團或l個頂的獨立集。具有這樣性質的最小自然數N就稱為一個拉姆齊數,記作R(k,l);
- 在着色理論中是這樣描述的:對於完全圖的任意一個2邊着色,使得中含有一個k階子完全圖,含有一個l階子完全圖,則稱滿足這個條件的最小的n為一個拉姆齊數。(注意:按照圖論的記法表示i階完全圖)
拉姆齊證明,對與給定的正整數數k及l,R(k,l)的答案是唯一和有限的。
拉姆齊數亦可推廣到多於兩個數:
- 對於完全圖的每條邊都任意塗上r種顏色之一,分別記為,在中,必定有個顏色為的階子完全圖,或有個顏色為的階子完全圖……或有個顏色為的階子完全圖。符合條件又最少的數n則記為。
數值或上下界
[編輯]已知的拉姆齊數非常少,保羅·艾狄胥曾以一個譬喻來描述尋找拉姆齊數的難度:「想像有隊外星人軍隊在地球降落,要求取得R(5,5)的值,否則便會毀滅地球。在這個情況,我們應該集中所有電腦和數學家嘗試去找這個數值。若他們要求的是R(6,6)的值,我們要嘗試毀滅這班外星人了。」[來源請求]
顯然易見的公式: R(0,s)=0, R(1,s)=1, R(2,s)=s, (將的順序改變並不改變拉姆齊的數值)。
s r
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 3 | 6 | 9 | 14 | 18 | 23 | 28 | 36 | 40–42 | ||
| 4 | 18 | 25[5] | 36–41 | 49–61 | 59[6]–84 | 73–115 | 92–149 | |||
| 5 | 43–48 | 58–87 | 80–143 | 101–216 | 133–316 | 149[6]–442 | ||||
| 6 | 102–165 | 115[6]–298 | 134[6]–495 | 183–780 | 204–1171 | |||||
| 7 | 205–540 | 217–1031 | 252–1713 | 292–2826 | ||||||
| 8 | 282–1870 | 329–3583 | 343–6090 | |||||||
| 9 | 565–6588 | 581–12677 | ||||||||
| 10 | 798–23556 |
組合電子期刊有不定期更新的動態綜述,介紹拉姆齊數的研究成果。[4]
漸近性質
[編輯]拉姆齊數滿足不等式。由此,利用數學歸納法,可以證明
其中誤差項o (1),當趨向於無窮時,趨向。
下界方面,1947年艾狄胥首創概率法,證明
雖然上下界皆是指數形式,但兩者底數不同,實際大小相差甚遠,如時,給出的界是。不過,截至2021年,上下界的底數仍毫無改進,依舊是和,僅有較低階項的改進。而且,下界依賴非構造性的概率方法,未有任何確切構造[註 2]能給出指數下界。暫時所知最佳結果為:
至於非對角拉姆齊數,已知其增長級別為;等價說法是,個頂點且無三角形的圖,獨立數的最小值用大Θ符號表示成
的上界由奧伊陶伊、科姆洛什、塞邁雷迪證出,而級的下界原先由金正翰(音譯)證明,其後格里菲斯、莫里斯、菲斯·龐蒂韋羅斯三人[7]和波曼、基瓦什兩人[8]藉分析「無三角形過程」,分別將下界獨立改進至
一般的非對角拉姆齊數,當固定而增大時,已知最優的上下界為
分別歸功於波曼、基瓦什兩人和奧伊陶伊、科姆洛什、塞邁雷迪三人。
延伸
[編輯]無窮圖
[編輯]本定理可引伸適用於無窮圖,同樣稱為拉姆齊定理。與有限圖的拉姆齊定理相提並論時,或稱無窮拉姆齊定理(Infinite Ramsey theorem)以作區分。
設為無窮集,以表示其兩兩所連邊的集合(即全體二元子集組成的族),每邊染成色之一。則存在同色無窮階完全圖,即有無窮子集,其邊集同色。[9][10]:1
證明:取任一。自引出無窮多條邊,必有某色出現無窮多次。記為該些邊另一端點的集合。又取任一,同樣自有無窮多條邊引至,故必有某色及無窮子集,使引至的各邊皆染色。
餘可類推,得到一列互異的元素及一列顏色。由於僅得有限多種色,必有顏色出現無窮多次,即有對於無窮序列成立。此時,有為無窮子集,且其元素兩兩連邊同色(因為邊所染為色),證畢。
關於無窮圖的二染色,艾狄胥-杜什尼克-米勒定理是較強的結果,但其中兩種顏色不對等。定理斷言,任意無窮圖(頂點數不必可數)的邊若染紅藍兩色,則或有可數無窮大的紅色完全子圖,或有與原圖同樣大的藍色完全子圖。[11]
無窮推出有限
[編輯]運用反證法,可以證明無窮拉姆齊定理推出有限拉姆齊定理。[12]
反設有限拉姆齊定理不成立,即某個拉姆齊數不存在,則有整數和滿足:對任意正整數,完全圖[註 3]皆有某種染色的方案,而不產生同色的元子集。以表示此種方案的集合。
對任意,可將中任意一種染色限制到子圖(即刪去頂點),不會額外產生同色的元子集,所以所得的染色仍在中。中,某些染色是以上述方式,由的染色限制而成,此種染色構成的子集,記為。由假設,非空,所以亦非空。
同樣,元素的限制必屬,故可定義為此種限制所得染色法的集合,其不為空。類推對所有正整數定義。
現對每個正整數,有,且逐個集合非空。又為有限集,因為由乘法原理,全體染色方案,不論是否有同色元集,總數是。由此,整個序列的交集非空。[註 4]又每個的元素來自某元素的限制,可知每個元素都來自元素的限制,從而由的染色出發,可以延拓成的染色,並可重複,直至得到無窮圖的染色,而無同色元集,與無窮拉姆齊定理矛盾。
以拓撲學觀之,此為標準的緊論證(compactness argument)[12],相當於考慮全體染色的拓撲空間,而由吉洪諾夫定理,其為若干個有限(從而緊)空間之積,所以仍為緊。而條件「在子圖上不產生同色元集」,描述該空間的一個閉開集,所以有限交非空推出全體交非空。
超圖
[編輯]定理亦可推廣至超圖。一個均勻超圖(或超圖)就是將圖的邊由二元子集換成元子集。超圖拉姆齊定理敍述如下:
對任意正整數和,以及任意正整數,存在拉姆齊數,使得階完全超圖的各邊,不論如何染種色,必存在令圖中可找出某個衹染色的階完全超圖。
此定理一般對歸納證出,的初始情況正如前文。
有向圖
[編輯]亦可定義有向圖的拉姆齊數,最早由P. Erdős and L. Moser (1964)提出。設為最小的正整數,使得階完全圖中,若為每邊賦兩種定向之一(所得有向圖稱為循環賽圖),則必有無圈的階循環賽圖[註 5] 。
此前定義為保證階完全無向圖染兩色會有同色完全階子圖的最小值,可見是的有向類比:兩種顏色現換成邊的兩種方向,而「同色」換成「全部邊方向統一」(所以無圈)。
註釋
[編輯]- ^ 有些作者如(Brualdi 2010)及(Harary 1972)要求,以免對單一頂點(從而無邊)的圖的邊染色。亦有(Gross 2008)和(Erdős & Szekeres 1935)等作者將兩種色換成有邊與否,從而定理敍述變成:在足夠大的簡單圖中,必有團或獨立集。此形式下或可更自然地考慮單頂點的圖。
- ^ 意即多項式時間算法的輸出結果。
- ^ 為方便起見,頂點集設為。
- ^ 考慮元素個數的最小值為何。
- ^ 又稱遞移(transitive)循環賽圖。
參考資料
[編輯]- ^ Ramsey, F. P. On a Problem of Formal Logic [論形式邏輯的一個問題]. Proceedings of the London Mathematical Society. 1930, s2–30 (1): 264–286. doi:10.1112/plms/s2-30.1.264 (英語).
- ^ Gleason, A. M.; Greenwood, R. E.; Kelly, L. M. (編). The William Lowell Putnam Mathematical Competition Problems and Solutions: 1938–1964 [威廉·羅威爾·普特南數學競賽問題和解答:1938-1964]. Mathematical Association of America. 1980: 38. ISBN 9780883854624 (英語).
- ^ Liu, Andy; Leigh, Robert Barrington (編). Hungarian Problem Book IV: Based on the Eötvös Competitions 1947–1963 [匈牙利問題集四:選自厄特沃什比賽1947-1963]. 2011: 1. ISBN 9780883858318. doi:10.5948/UPO9781614444053 (英語).
- ^ 4.0 4.1 Radziszowski, Stanisław. Small Ramsey Numbers [小拉姆齊數]. The Electronic Journal of Combinatorics. 2021-01-15. 1994-08-01 [2021-12-29]. doi:10.37236/21. (原始內容存檔於2022-04-07) (英語).
- ^ Brendan D. McKay, Stanislaw P. Radziszowski. R(4,5) = 25 (PDF). Journal of Graph Theory. May 1995, 19 (3): 309–322 [2019-01-05]. doi:10.1002/jgt.3190190304. (原始內容存檔 (PDF)於2021-02-25).
- ^ 6.0 6.1 6.2 6.3 Exoo, Geoffrey; Tatarevic, Milos. New Lower Bounds for 28 Classical Ramsey Numbers. The Electronic Journal of Combinatorics. 2015, 22 (3): 3 [2018-09-02]. (原始內容存檔於2021-02-28).
- ^ Fiz Pontiveros, Gonzalo; Griffiths, Simon; Morris, Robert. The Triangle-Free Process and the Ramsey Number R(3, t) [無三角形過程與拉姆齊數R(3, t)]. Memoirs of the American Mathematical Society. 2020, 263 (1274) [2013]. arXiv:1302.6279
 . doi:10.1090/memo/1274 (英語).
. doi:10.1090/memo/1274 (英語).
- ^ Bohman, Tom; Keevash, Peter. Dynamic concentration of the triangle-free process [無三角形過程的動力集中性]. The Seventh European Conference on Combinatorics, Graph Theory and Applications. CRM Series (Pisa: Edizioni della Normale). 2013, 16. arXiv:1302.5963
 . doi:10.1007/978-88-7642-475-5_78 (英語).
. doi:10.1007/978-88-7642-475-5_78 (英語).
- ^ 9.0 9.1 Martin Gould. Ramsey Theory [拉姆齊理論] (PDF). [2021-12-20]. (原始內容 (PDF)存檔於2021-11-26) (英語).
- ^ 10.0 10.1 I. B. Leader (Lecture notes taken by P. A. Russell). Ramsey Theory [拉姆齊理論] (PDF). [2021-12-20]. (原始內容 (PDF)存檔於2022-01-21) (英語).
- ^ Dushnik, Ben; Miller, E. W. Partially ordered sets [偏序集]. American Journal of Mathematics. 1941, 63 (3): 600–610. JSTOR 2371374. MR 0004862. doi:10.2307/2371374. hdl:10338.dmlcz/100377
 (英語). 尤其見定理5.22與5.23。
(英語). 尤其見定理5.22與5.23。
- ^ 12.0 12.1 Diestel, Reinhard. Chapter 8, Infinite Graphs [第8章:無窮圖]. Graph Theory [圖論] 4. Heidelberg: Springer-Verlag. 2010: 209–2010. ISBN 978-3-662-53621-6 (英語).
- ^ Smith, Warren D.; Exoo, Geoff. Partial Answer to Puzzle #27: A Ramsey-like quantity [謎題27的部分解:某拉姆齊類數]. [2020-06-02]. (原始內容存檔於2021-11-26) (英語).
- ^ Neiman, David; Mackey, John; Heule, Marijn. Tighter Bounds on Directed Ramsey Number R(7) [有向拉姆齊數R(7)較緊的界]. 2020-11-01. arXiv:2011.00683
 [math.CO] (英語).
[math.CO] (英語).
參考文獻
[編輯]- Ajtai, Miklós; Komlós, János; Szemerédi, Endre, A note on Ramsey numbers, J. Combin. Theory Ser. A, 1980, 29 (3): 354–360, doi:10.1016/0097-3165(80)90030-8
 .
. - Bohman, Tom; Keevash, Peter, The early evolution of the H-free process, Invent. Math., 2010, 181 (2): 291–336, Bibcode:2010InMat.181..291B, S2CID 2429894, arXiv:0908.0429
 , doi:10.1007/s00222-010-0247-x
, doi:10.1007/s00222-010-0247-x - Brualdi, Richard A., Introductory Combinatorics 5th, Prentice-Hall: 77–82, 2010, ISBN 978-0-13-602040-0
- Conlon, David, A new upper bound for diagonal Ramsey numbers, Annals of Mathematics, 2009, 170 (2): 941–960, MR 2552114, S2CID 9238219, arXiv:math/0607788v1
 , doi:10.4007/annals.2009.170.941.
, doi:10.4007/annals.2009.170.941. - Erdős, Paul, Some remarks on the theory of graphs, Bull. Amer. Math. Soc., 1947, 53 (4): 292–294, doi:10.1090/S0002-9904-1947-08785-1
 .
. - Erdős, P.; Moser, L., On the representation of directed graphs as unions of orderings (PDF), A Magyar Tudományos Akadémia, Matematikai Kutató Intézetének Közleményei, 1964, 9: 125–132 [2023-11-06], MR 0168494, (原始內容存檔 (PDF)於2022-12-23)
- Erdős, Paul; Szekeres, George, A combinatorial problem in geometry (PDF), Compositio Mathematica, 1935, 2: 463–470 [2023-11-06], ISBN 978-0-8176-4841-1, doi:10.1007/978-0-8176-4842-8_3, (原始內容存檔 (PDF)於2023-11-06).
- Exoo, G., A lower bound for R(5,5), Journal of Graph Theory, 1989, 13: 97–98, doi:10.1002/jgt.3190130113.
- Graham, R.; Rothschild, B.; Spencer, J. H., Ramsey Theory, New York: John Wiley and Sons, 1990.
- Gross, Jonathan L., Combinatorial Methods with Computer Applications, CRC Press: 458, 2008, ISBN 978-1-58488-743-0
- Harary, Frank, Graph Theory, Addison-Wesley: 16–17, 1972, ISBN 0-201-02787-9
- Ramsey, F. P., On a problem of formal logic, Proceedings of the London Mathematical Society, 1930, 30: 264–286, doi:10.1112/plms/s2-30.1.264.
- Spencer, J., Ramsey's theorem – a new lower bound, J. Combin. Theory Ser. A, 1975, 18: 108–115, doi:10.1016/0097-3165(75)90071-0
 .
. - Bian, Zhengbing; Chudak, Fabian; Macready, William G.; Clark, Lane; Gaitan, Frank, Experimental determination of Ramsey numbers, Physical Review Letters, 2013, 111 (13): 130505, Bibcode:2013PhRvL.111m0505B, PMID 24116761, S2CID 1303361, arXiv:1201.1842
 , doi:10.1103/PhysRevLett.111.130505.
, doi:10.1103/PhysRevLett.111.130505.















































![{\displaystyle K_{n}[e_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9c117adca3edb065591aa91f65a9dac25c5544)
![{\displaystyle K_{n}[e_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5434beb86c250517b47ae893a89270aabd9c51ea)














![{\displaystyle R(s,s)\leq [1+o(1)]{\frac {4^{s-1}}{\sqrt {\pi s}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54309362045ded2d8e457fe3bc2b3a07ef0d7c1e)


![{\displaystyle R(s,s)\geq [1+o(1)]{\frac {s}{{\sqrt {2}}e}}2^{s/2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5172a4a6604ed18ab00f11b6aba4e1f42f448fdf)




![{\displaystyle [1+o(1)]{\frac {{\sqrt {2}}s}{e}}2^{\frac {s}{2}}\leq R(s,s)\leq s^{-(c\log s)/(\log \log s)}4^{s},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98d3d42edf70185ccfa40a6b0153b034f595e9e1)
































![{\displaystyle [k]^{(2)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/106a8077b76a809bbed39f3ed292b6218a1020fe)
















![{\displaystyle [c]^{\binom {\mathbb {N} }{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da6ee9d1d1e341476337bdf31c97c56fe856d26f)
![{\displaystyle [c]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a864aec9ea68d53f65cd151cbb0d662c5e5ddc1)

















![{\displaystyle [k]=\{1,2,3,\ldots ,k\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b15c1f7e7f8f3c7d036959751c77fe3815e1ad4)