積 (範疇論)
外觀
範疇論中,積(或直積)的概念提取了集合的笛卡兒積、群的積、環的積、拓撲空間的積等概念的共性。本質上講,一組對象的積是到這些對象都有態射的對象中最具代表性的。
定義
[編輯]給定範疇C。C中一對象集{Xi | i ∈ I}的積為滿足下面泛性質的偶(X, (πi)),其中X為一對象,πi : X → Xi(i ∈ I)為一組態射:對任意對象Y及其到Xi的一組態射fi,存在唯一的態射f : Y → X滿足,對任意i ∈ I,fi = πi f。即,對任意i,下圖可交換。

若該組對象僅有兩個,積通常用X1×X2來表示。上圖變為:
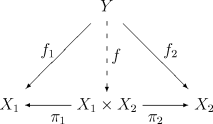
此時,此唯一態射f也常表示為<f1,f2>。
討論
[編輯]積為範疇論中的一種極限。積也即C中離散子範疇的極限。積不一定存在。但若存在,則由其定義易知其在同構的意義下唯一。
若C中對任意基於I的對象集均存在積,則該積也可以看做一個從CI到C的函子。
集合{Xi}的積通常記為∏i Xi。態射πi也稱為自然投影。如下自然同構成立:
(HomC(U,V)表示C中從U到V的態射集;左側的積為範疇意義上的積、右側的為集合的笛卡兒積)。
若I為有限集,例如I = {1,...,n},則X1,...,Xn的積通常記為X1×...×Xn。
設C存在有限積,採用上述積函子的定義,並用1表示C的終對象(空積),則下列自然同構成立:
上述為構成一個交換么半群的條件。
舉例
[編輯]- Set的積為集合的笛卡兒積。
- 由偏序構成的範疇:一組元素的積為該組元素的最大下界。
參見
[編輯]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





