用戶:Atry/特徵選擇

在機器學習和統計學中，特徵選擇 也被稱為變量選擇 , 屬性選擇 或變量子集選擇 。它是指：為了構建模型而選擇相關特徵（即屬性、指標）子集的過程。使用特徵選擇技術有三個原因：

• 簡化模型，使之更易於被研究人員或用戶理解，
• 縮短訓練時間，
• 改善通用性、降低過擬合（即降低方差 ）

要使用特徵選擇技術的關鍵假設是：訓練數據包含許多冗餘 或無關 的特徵，因而移除這些特徵並不會導致丟失信息。 冗餘 或無關 特徵是兩個不同的概念。如果一個特徵本身有用，但如果這個特徵與另一個有用特徵強相關，且那個特徵也出現在數據中，那麼這個特徵可能就變得多餘。

特徵選擇技術與特徵提取有所不同。特徵提取是從原有特徵的功能中創造新的特徵，而特徵選擇則只返回原有特徵中的子集。 特徵選擇技術的常常用於許多特徵但樣本（即數據點）相對較少的領域。特徵選擇應用的典型用例包括：解析書面文本和微陣列數據，這些場景下特徵成千上萬，但樣本只有幾十到幾百個。

介紹

特徵選擇算法可以被視為搜索技術和評價指標的結合。前者提供候選的新特徵子集，後者為不同的特徵子集打分。 最簡單的算法是測試每個特徵子集，找到究竟哪個子集的錯誤率最低。這種算法需要窮舉搜索空間，難以算完所有的特徵集，只能涵蓋很少一部分特徵子集。 選擇何種評價指標很大程度上影響了算法。而且，通過選擇不同的評價指標，可以吧特徵選擇算法分為三類：包裝類、過濾類和嵌入類方法

包裝類方法使用預測模型給特徵子集打分。每個新子集都被用來訓練一個模型，然後用驗證數據集來測試。通過計算驗證數據集上的錯誤次數（即模型的錯誤率）給特徵子集評分。由於包裝類方法為每個特徵子集訓練一個新模型，所以計算量很大。不過，這類方法往往能為特定類型的模型找到性能最好的特徵集。

過濾類方法採用代理指標，而不根據特徵子集的錯誤率計分。所選的指標算得快，但仍然能估算出特徵集好不好用。常用指標包括互信息、逐點互信息, 皮爾遜積矩相關係數、每種分類/特徵的組合的幀間/幀內類距離或顯著性測試評分。

過濾類方法計算量一般比包裝類小，但這類方法找到的特徵子集不能為特定類型的預測模型調校。由於缺少調校，過濾類方法所選取的特徵集會比包裝類選取的特徵集更為通用，往往會導致比包裝類的預測性能更為低下。不過，由於特徵集不包含對預測模型的假設，更有利於暴露特徵之間的關係。許多過濾類方法提供特徵排名，而非顯式提供特徵子集。要從特徵列表的哪個點切掉特徵，得靠交叉驗證來決定。過濾類方法也常常用於包裝方法的預處理步驟，以便在問題太複雜時依然可以用包裝方法。

嵌入類方法包括了所有構建模型過程中庸道德特徵選擇技術。這類方法的典範是構建線性模型的LASSO方法。該方法給回歸係數加入了L1懲罰，導致其中的許多參數趨於零。任何回歸係數不為零的特徵都會被LASSO算法「選中」。LASSO的改良算法有Bolasso和FeaLect。Bolasso改進了樣本的初始過程。FeaLect根據回歸係數組合分析給所有特徵打分。 另外一個流行的做法是遞歸特徵消除（Recursive Feature Elimination）算法，通常用於支持向量機，通過反覆構建同一個模型移除低權重的特徵。這些方法的計算複雜度往往在過濾類和包裝類之間。

傳統的統計學中，特徵選擇的最普遍的形式是逐步回歸，這是一個包裝類技術。它屬於貪心算法，每一輪添加該輪最優的特徵或者刪除最差的特徵。主要的調控因素是決定何時停止算法。在機器學習領域，這個時間點通常通過交叉驗證找出。在統計學中，某些條件已經優化。因而會導致嵌套引發問題。此外，還有更健壯的方法，如分支和約束和分段線性網絡。

Subset selection

Subset selection evaluates a subset of features as a group for suitability. Subset selection algorithms can be broken up into Wrappers, Filters and Embedded. Wrappers use a search algorithm to search through the space of possible features and evaluate each subset by running a model on the subset. Wrappers can be computationally expensive and have a risk of over fitting to the model. Filters are similar to Wrappers in the search approach, but instead of evaluating against a model, a simpler filter is evaluated. Embedded techniques are embedded in and specific to a model.

Many popular search approaches use greedy hill climbing, which iteratively evaluates a candidate subset of features, then modifies the subset and evaluates if the new subset is an improvement over the old. Evaluation of the subsets requires a scoring metric that grades a subset of features. Exhaustive search is generally impractical, so at some implementor (or operator) defined stopping point, the subset of features with the highest score discovered up to that point is selected as the satisfactory feature subset. The stopping criterion varies by algorithm; possible criteria include: a subset score exceeds a threshold, a program's maximum allowed run time has been surpassed, etc.

Alternative search-based techniques are based on targeted projection pursuit which finds low-dimensional projections of the data that score highly: the features that have the largest projections in the lower-dimensional space are then selected.

Search approaches include:

• Exhaustive
• Best first
• Simulated annealing
• 這些理論包括：
• Greedy forward selection
• Greedy backward elimination
• Particle swarm optimization
• Targeted projection pursuit
• Scatter Search
• Variable Neighborhood Search

Two popular filter metrics for classification problems are correlation and mutual information, although neither are true metrics or 'distance measures' in the mathematical sense, since they fail to obey the triangle inequality and thus do not compute any actual 'distance' – they should rather be regarded as 'scores'. These scores are computed between a candidate feature (or set of features) and the desired output category. There are, however, true metrics that are a simple function of the mutual information; see here.

Other available filter metrics include:

• Class separability
  • Error probability
  • Inter-class distance
  • Probabilistic distance
  • Entropy
• Consistency-based feature selection
• Correlation-based feature selection

Optimality criteria

The choice of optimality criteria is difficult as there are multiple objectives in a feature selection task. Many common ones incorporate a measure of accuracy, penalised by the number of features selected (e.g. the Bayesian information criterion). The oldest are Mallows's C_p statistic and Akaike information criterion (AIC). These add variables if the t -statistic is bigger than ${\sqrt {2}}$.

Other criteria are Bayesian information criterion (BIC) which uses ${\sqrt {\log {n}}}$, minimum description length (MDL) which asymptotically uses ${\sqrt {\log {n}}}$, Bonferroni / RIC which use ${\sqrt {2\log {p}}}$, maximum dependency feature selection, and a variety of new criteria that are motivated by false discovery rate (FDR) which use something close to ${\sqrt {2\log {\frac {p}{q}}}}$.

Structure Learning

Filter feature selection is a specific case of a more general paradigm called Structure Learning. Feature selection finds the relevant feature set for a specific target variable whereas structure learning finds the relationships between all the variables, usually by expressing these relationships as a graph. The most common structure learning algorithms assume the data is generated by a Bayesian Network, and so the structure is a directed graphical model. The optimal solution to the filter feature selection problem is the Markov blanket of the target node, and in a Bayesian Network, there is a unique Markov Blanket for each node.

Minimum-redundancy-maximum-relevance (mRMR) feature selection

Peng et al. proposed a feature selection method that can use either mutual information, correlation, or distance/similarity scores to select features. The aim is to penalise a feature's relevancy by its redundancy in the presence of the other selected features. The relevance of a feature set S for the class c is defined by the average value of all mutual information values between the individual feature f_i and the class c as follows:

$D(S,c)={\frac {1}{|S|}}\sum _{f_{i}\in S}I(f_{i};c)$.

The redundancy of all features in the set S is the average value of all mutual information values between the feature f_i and the feature f_j:

$R(S)={\frac {1}{|S|^{2}}}\sum _{f_{i},f_{j}\in S}I(f_{i};f_{j})$

The mRMR criterion is a combination of two measures given above and is defined as follows:

$\mathrm {mRMR} =\max _{S}\left[{\frac {1}{|S|}}\sum _{f_{i}\in S}I(f_{i};c)-{\frac {1}{|S|^{2}}}\sum _{f_{i},f_{j}\in S}I(f_{i};f_{j})\right].$

Suppose that there are n full-set features. Let x_i be the set membership indicator function for feature f_i, so that x_i=1 indicates presence and x_i=0 indicates absence of the feature f_i in the globally optimal feature set. Let $c_{i}=I(f_{i};c)$ and $a_{ij}=I(f_{i};f_{j})$. The above may then be written as an optimization problem:

$\mathrm {mRMR} =\max _{x\in \{0,1\}^{n}}\left[{\frac {\sum _{i=1}^{n}c_{i}x_{i}}{\sum _{i=1}^{n}x_{i}}}-{\frac {\sum _{i,j=1}^{n}a_{ij}x_{i}x_{j}}{(\sum _{i=1}^{n}x_{i})^{2}}}\right].$

The mRMR algorithm is an approximation of the theoretically optimal maximum-dependency feature selection algorithm that maximizes the mutual information between the joint distribution of the selected features and the classification variable. As mRMR approximates the combinatorial estimation problem with a series of much smaller problems, each of which only involves two variables, it thus uses pairwise joint probabilities which are more robust. In certain situations the algorithm may underestimate the usefulness of features as it has no way to measure interactions between features which can increase relevancy. This can lead to poor performance when the features are individually useless, but are useful when combined (a pathological case is found when the class is a parity function of the features). Overall the algorithm is more efficient (in terms of the amount of data required) than the theoretically optimal max-dependency selection, yet produces a feature set with little pairwise redundancy.

mRMR is an instance of a large class of filter methods which trade off between relevancy and redundancy in different ways.

Global optimization formulations

mRMR is a typical example of an incremental greedy strategy for feature selection: once a feature has been selected, it cannot be deselected at a later stage. While mRMR could be optimized using floating search to reduce some features, it might also be reformulated as a global quadratic programming optimization problem as follows:

$\mathrm {QPFS} :\min _{\mathbf {x} }\left\{\alpha \mathbf {x} ^{T}H\mathbf {x} -\mathbf {x} ^{T}F\right\}\quad {\mbox{s.t.}}\ \sum _{i=1}^{n}x_{i}=1,x_{i}\geq 0$

where $F_{n\times 1}=[I(f_{1};c),\ldots ,I(f_{n};c)]^{T}$ is the vector of feature relevancy assuming there are n features in total, $H_{n\times n}=[I(f_{i};f_{j})]_{i,j=1\ldots n}$ is the matrix of feature pairwise redundancy, and $\mathbf {x} _{n\times 1}$ represents relative feature weights. QPFS is solved via quadratic programming. It is recently shown that QFPS is biased towards features with smaller entropy, due to its placement of the feature self redundancy term $I(f_{i};f_{i})$ on the diagonal of H.

Another global formulation for the mutual information based feature selection problem is based on the conditional relevancy:

$\mathrm {SPEC_{CMI}} :\max _{\mathbf {x} }\left\{\mathbf {x} ^{T}Q\mathbf {x} \right\}\quad {\mbox{s.t.}}\ \|\mathbf {x} \|=1,x_{i}\geq 0$

where $Q_{ii}=I(f_{i};c)$ and $Q_{ij}=I(f_{i};c|f_{j}),i\neq j$.

An advantage of SPEC_CMI is that it can be solved simply via finding the dominant eigenvector of Q, thus is very scalable. SPEC_CMI also handles second-order feature interaction.

For high-dimensional and small sample data (e.g., dimensionality > 10^{7000500000000000000♠5} and the number of samples < 10^{7000300000000000000♠3}), the Hilbert-Schmidt Independence Criterion Lasso (HSIC Lasso) is useful. HSIC Lasso optimization problem is given as

$\mathrm {HSIC_{Lasso}} :\min _{\mathbf {x} }{\frac {1}{2}}\sum _{k,l=1}^{n}x_{k}x_{l}{\mbox{HSIC}}(f_{k},f_{l})-\sum _{k=1}^{n}x_{k}{\mbox{HSIC}}(f_{k},c)+\lambda \|\mathbf {x} \|_{1},\quad {\mbox{s.t.}}\ x_{1},\ldots ,x_{n}\geq 0,$

where ${\mbox{HSIC}}(f_{k},c)={\mbox{tr}}({\bar {\mathbf {K} }}^{(k)}{\bar {\mathbf {L} }})$ is a kernel-based independence measure called the (empirical) Hilbert-Schmidt independence criterion (HSIC), ${\mbox{tr}}(\cdot )$ denotes the trace, $\lambda$ is the regularization parameter, ${\bar {\mathbf {K} }}^{(k)}=\mathbf {\Gamma } \mathbf {K} ^{(k)}\mathbf {\Gamma }$ and ${\bar {\mathbf {L} }}=\mathbf {\Gamma } \mathbf {L} \mathbf {\Gamma }$ are input and output centered Gram matrices, $K_{i,j}^{(k)}=K(u_{k,i},u_{k,j})$ and $L_{i,j}=L(c_{i},c_{j})$ are Gram matrices, $K(u,u')$ and $L(c,c')$ are kernel functions, $\mathbf {\Gamma } =\mathbf {I} _{m}-{\frac {1}{m}}\mathbf {1} _{m}\mathbf {1} _{m}^{T}$ is the centering matrix, $\mathbf {I} _{m}$ is the m-dimensional identity matrix (m: the number of samples), $\mathbf {1} _{m}$ is the m-dimensional vector with all ones, and $\|\cdot \|_{1}$ is the $\ell _{1}$-norm. HSIC always takes a non-negative value, and is zero if and only if two random variables are statistically independent when a universal reproducing kernel such as the Gaussian kernel is used.

The HSIC Lasso can be written as

$\mathrm {HSIC_{Lasso}} :\min _{\mathbf {x} }{\frac {1}{2}}\left\|{\bar {\mathbf {L} }}-\sum _{k=1}^{n}x_{k}{\bar {\mathbf {K} }}^{(k)}\right\|_{F}^{2}+\lambda \|\mathbf {x} \|_{1},\quad {\mbox{s.t.}}\ x_{1},\ldots ,x_{n}\geq 0,$

where $\|\cdot \|_{F}$ is the Frobenius norm. The optimization problem is a Lasso problem, and thus it can be efficiently solved with a state-of-the-art Lasso solver such as the dual augmented Lagrangian method.

Correlation feature selection

The Correlation Feature Selection (CFS) measure evaluates subsets of features on the basis of the following hypothesis: "Good feature subsets contain features highly correlated with the classification, yet uncorrelated to each other". The following equation gives the merit of a feature subset S consisting of k features:

$Merit_{S_{k}}={\frac {k{\overline {r_{cf}}}}{\sqrt {k+k(k-1){\overline {r_{ff}}}}}}.$

Here, ${\overline {r_{cf}}}$ is the average value of all feature-classification correlations, and ${\overline {r_{ff}}}$ is the average value of all feature-feature correlations. The CFS criterion is defined as follows:

$\mathrm {CFS} =\max _{S_{k}}\left[{\frac {r_{cf_{1}}+r_{cf_{2}}+\cdots +r_{cf_{k}}}{\sqrt {k+2(r_{f_{1}f_{2}}+\cdots +r_{f_{i}f_{j}}+\cdots +r_{f_{k}f_{1}})}}}\right].$

The $r_{cf_{i}}$ and $r_{f_{i}f_{j}}$ variables are referred to as correlations, but are not necessarily Pearson's correlation coefficient or Spearman's ρ. Dr. Mark Hall's dissertation uses neither of these, but uses three different measures of relatedness, minimum description length (MDL), symmetrical uncertainty, and relief.

Let x_i be the set membership indicator function for feature f_i ; then the above can be rewritten as an optimization problem:

$\mathrm {CFS} =\max _{x\in \{0,1\}^{n}}\left[{\frac {(\sum _{i=1}^{n}a_{i}x_{i})^{2}}{\sum _{i=1}^{n}x_{i}+\sum _{i\neq j}2b_{ij}x_{i}x_{j}}}\right].$

The combinatorial problems above are, in fact, mixed 0–1 linear programming problems that can be solved by using branch-and-bound algorithms.

Regularized trees

The features from a decision tree or a tree ensemble are shown to be redundant. A recent method called regularized tree can be used for feature subset selection. Regularized trees penalize using a variable similar to the variables selected at previous tree nodes for splitting the current node. Regularized trees only need build one tree model (or one tree ensemble model) and thus are computationally efficient.

Regularized trees naturally handle numerical and categorical features, interactions and nonlinearities. They are invariant to attribute scales (units) and insensitive to outliers, and thus, require little data preprocessing such as normalization. Regularized random forest (RRF) is one type of regularized trees. The guided RRF is an enhanced RRF which is guided by the importance scores from an ordinary random forest.

Overview on metaheuristics methods

A metaheuristic is a general description of an algorithm dedicated to solve difficult (typically NP-hard problem) optimization problems for which there is no classical solving methods. Generally, a metaheuristic is a stochastics algorithm tending to reach a global optima. There are many metaheuristics, from a simple local search to a complex global search algorithm.

Main principles

The feature selection methods are typically presented in three classes based on how they combine the selection algorithm and the model building.

Filter Method

Filter Method for feature selection

Filter-based feature selection has become crucial in many classification settings, especially object recognition, recently faced with feature learning strategies that originate thousands of cues. Filter methods analyze intrinsic properties of data, ignoring the classifier. Most of these methods can perform two operations, ranking and subset selection: in the former, the importance of each individual feature is evaluated, usually by neglecting potential interactions among the elements of the joint set; in the latter, the final subset of features to be selected is provided. In some cases, these two operations are performed sequentially (first the ranking, then the selection); in other cases, only the selection is carried out. Filter methods suppress the least interesting variables. These methods are particularly effective in computation time and robust to overfitting.

However, filter methods tend to select redundant variables because they do not consider the relationships between variables. Therefore, they are mainly used as a pre-process method.

Wrapper Method

Wrapper Method for Feature selection

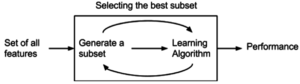
Wrapper methods evaluate subsets of variables which allows, unlike filter approaches, to detect the possible interactions between variables. The two main disadvantages of these methods are :

• The increasing overfitting risk when the number of observations is insufficient.
• The significant computation time when the number of variables is large.

Embedded Method

Embedded method for Feature selection

Recently, embedded methods have been proposed to reduce the classification of learning. They try to combine the advantages of both previous methods. The learning algorithm takes advantage of its own variable selection algorithm. So, it needs to know preliminary what a good selection is, which limits their exploitation.

Application of feature selection metaheuristics

This is a survey of the application of feature selection metaheuristics lately used in the literature. This survey was realized by J. Hammon in her thesis.

應用領域	算法	我們的工作方式	classifier	Evaluation Function	{0}參考號{1}：016596{/1}{/0}
SNPs	Feature Selection using Feature Similarity	過濾		ŕ	Phuong 2005
SNPs	這些理論包括：	{0}wrapper{/0}{1}.{/1}	Decision Tree	Classification accuracy (10-fold)	Shah 2004
SNPs	HillClimbing	Filter + Wrapper	Naive Bayesian	Predicted residual sum of squares	長
SNPs	Simulated Annealing		Naive bayesian	Classification accuracy (5-fold)	Ustunkar 2011
Segments parole	Ants colony	{0}wrapper{/0}{1}.{/1}	Artificial Neural Network	MSE	Al-ani 2005
營銷	Simulated Annealing	{0}wrapper{/0}{1}.{/1}	回歸	AIC, r2	Meiri 2006
經濟	Simulated Annealing, Genetic Algorithm	{0}wrapper{/0}{1}.{/1}	回歸	BIC	Kapetanios 2005
Spectral Mass	這些理論包括：	{0}wrapper{/0}{1}.{/1}	Multiple Linear Regression, Partial Least Squares	root-mean-square error of prediction	Broadhurst 2007
Microarray	Tabu Search + PSO	{0}wrapper{/0}{1}.{/1}	Support Vector Machine, K Nearest Neighbors	Euclidean Distance	Chuang 2009
Microarray	PSO + Genetic Algorithm	{0}wrapper{/0}{1}.{/1}	Support Vector Machine	Classification accuracy (10-fold)	Alba 2007
Microarray	Genetic Algorithm + Iterated Local Search	EMBEDDED	Support Vector Machine	Classification accuracy (10-fold)	Duval 2009
Microarray	Iterated Local Search	{0}wrapper{/0}{1}.{/1}	回歸	Posterior Probability	Hans 2007
Microarray	這些理論包括：	{0}wrapper{/0}{1}.{/1}	K Nearest Neighbors	Classification accuracy (Leave-one-out cross-validation)	Jirapech-Umpai 2005
Microarray	Hybrid Genetic Algorithm	{0}wrapper{/0}{1}.{/1}	K Nearest Neighbors	Classification accuracy (Leave-one-out cross-validation)	我
Microarray	這些理論包括：	{0}wrapper{/0}{1}.{/1}	Support Vector Machine	Sensitivity and specificity	Xuan 2011
Microarray	這些理論包括：	{0}wrapper{/0}{1}.{/1}	All paired Support Vector Machine	Classification accuracy (Leave-one-out cross-validation)	Peng 2003
Microarray	這些理論包括：	EMBEDDED	Support Vector Machine	Classification accuracy (10-fold)	Hernandez 2007
Microarray	這些理論包括：	混合式	Support Vector Machine	Classification accuracy (Leave-one-out cross-validation)	Huerta 2006
Microarray	這些理論包括：		Support Vector Machine	Classification accuracy (10-fold)	Muni 2006
Microarray	這些理論包括：	{0}wrapper{/0}{1}.{/1}	Support Vector Machine	EH-DIALL, CLUMP	Jourdan 2004
Object Recognition	Infinite Feature Selection	過濾	Support Vector Machine	Mean Average Precision (mAP)	Roffo 2015

Feature selection embedded in learning algorithms

Some learning algorithms perform feature selection as part of their overall operation. 這些心理素質包括:

• $l_{1}$-regularization techniques, such as sparse regression, LASSO, and $l_{1}$-SVM
• Regularized trees, e.g. regularized random forest implemented in the RRF package
• Decision tree
• Memetic algorithm
• Random multinomial logit (RMNL)
• Auto-encoding networks with a bottleneck-layer
• Submodular feature selection

參見

• 群集分析
• Dimensionality reduction
• Feature extraction
• · 數據挖掘

擴展閱讀

• Feature Selection for Classification: A Review (Survey,2014)
• Feature Selection for Clustering: A Review (Survey,2013)
• Tutorial Outlining Feature Selection Algorithms, Arizona State University
• JMLR Special Issue on Variable and Feature Selection
• Feature Selection for Knowledge Discovery and Data Mining (Book)
• An Introduction to Variable and Feature Selection (Survey)
• Toward integrating feature selection algorithms for classification and clustering (Survey)
• feature subset selection and subset size optimization.pdf Efficient Feature Subset Selection and Subset Size Optimization (Survey, 2010)
• Searching for Interacting Features
• Feature Subset Selection Bias for Classification Learning
• Y. Sun, S. Todorovic, S. Goodison, Local Learning Based Feature Selection for High-dimensional Data Analysis, IEEE Transactions on Pattern Analysis and Machine Intelligence , vol. 32, no. 9, pp. {0}8.{/0} {1}{/1}

外部連結

• A comprehensive package for Mutual Information based feature selection in Matlab
• Infinite Feature Selection (Source Code) in Matlab
• Feature Selection Package, Arizona State University (Matlab Code)
• NIPS challenge 2003 (see also NIPS)
• Naive Bayes implementation with feature selection in Visual Basic (includes executable and source code)
• Minimum-redundancy-maximum-relevance (mRMR) feature selection program
• FEAST (Open source Feature Selection algorithms in C and MATLAB)

[[Category:{0}3{/0}{1}     {/1}{0}模型選擇{/0}]]