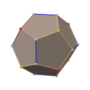
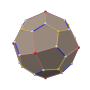
筝形六十面体
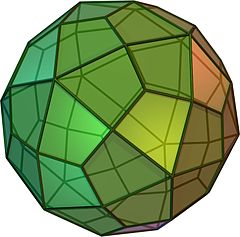 (按这里观看旋转模型) | ||||
| 类别 | 卡塔兰立体 六十面体 | |||
|---|---|---|---|---|
| 对偶多面体 | 小斜方截半二十面体 | |||
| 识别 | ||||
| 鲍尔斯缩写 | sladit | |||
| 数学表示法 | ||||
| 考克斯特符号 | ||||
| 康威表示法 | oD 或 deD | |||
| 性质 | ||||
| 面 | 60 | |||
| 边 | 120 | |||
| 顶点 | 62 | |||
| 欧拉特征数 | F=60, E=120, V=62 (χ=2) | |||
| 二面角 | 154° 7′ 17′′ arccos(-19-8√5/41) | |||
| 组成与布局 | ||||
| 面的种类 |  筝形 | |||
| 面的布局 | V3.4.5.4 | |||
| 顶点的种类 | 20个3阶顶点 30个4阶顶点 12个5阶顶点 | |||
| 对称性 | ||||
| 对称群 | Ih, H3, [5,3], (*532) | |||
| 旋转对称群 | I, [5,3]+, (532) | |||
| 图像 | ||||
| ||||
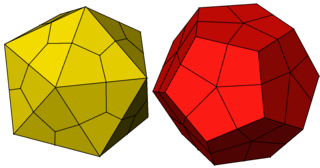
在几何学中,筝形六十面体是一种卡塔兰立体,由60个全等的筝形组成,是小斜方截半二十面体的对偶多面体,其拓朴结构与菱形六十面体相同[1],是6个不存在哈密顿路径的卡塔兰立体之一。[2]在图论中,筝形六十面体与菱形六十面体皆对应到筝形六十面体图,也就是说筝形六十面体与菱形六十面体与拓朴同构[3]。
性质
[编辑]筝形六十面体由60个面、120条边和62个顶点组成。[4]其中,60个面都是全等的筝形。在其62个顶点中,有20个顶点是3个筝形的公共顶点、30个顶点是4个筝形的公共顶点和12个顶点是5个筝形的公共顶点[5],这三种顶点分别可以对应到其对偶多面体小斜方截半二十面体的三种面上[6] 。筝形六十面体不存在哈密顿路径[2],换句话说,即在筝形六十面体中找不到一条沿着筝形六十面体的边,恰好通过每个顶点、且不重复拜访顶点的路径[7]。
面的组成
[编辑]组成筝形六十面体的筝形,若将短边长定为单位长,则其长边为:[8]
换句话说即短边长与长边长的比为1:7 + √5/6 ≈ 1:1.539344663...;反过来,长边长与短边长的比为1:3(7-√5)/22 ≈ 1:0.64962709397。[9]
二面角
[编辑]筝形六十面体只有一种二面角,其值为负41分之19与八倍的五平方根之和的反余弦值:[5]
尺寸
[编辑]最短边边长为单位长的筝形六十面体,其表面积和体积为:[10]
其内切球半径是一个四次式的根。这个四次式为:[11]
正交投影
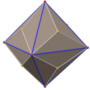
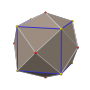
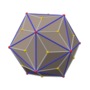
[编辑]筝形六十面体有3种具对称性的投影位置,分别位于其三种顶点上。其中最后两种的对偶图之对称性对应于A2和H2的考克斯特平面[13]。
| 投影对称性 | [2] | [2] | [2] | [2] | [6] | [10] |
|---|---|---|---|---|---|---|
| 图像 | 
|

|

|

|

|

|
| 对偶图像 | 
|

|

|

|

|

|
变体
[编辑]筝形六十面体可以透过在正二十面体或正十二面体的面中心加入顶点,并加入从新顶点到原始边的新边来构造,[14]因此筝形六十面体在康威多面体表示法中可以用oI或oD来表示[15]。这种几何变换存在一个能连续变化的自由度,因此可以产生许多变体。以从正二十面体构建的版本为例,三角形中心加入顶点连接到边缘可以是垂直于边缘或著不垂直于边缘,这将产生两种不同的筝形六十面体变体。[14]
用途
[编辑]由于筝形六十面体每个面都是相同的筝形[16],因此有时会被用于制作六十面的骰子[17][18]。此外,在化学中,分子Au42N20模型呈筝形六十面体,并具有一定程度的稳定性。[19]
-
筝形六十面体的骰子
参见
[编辑]参考文献
[编辑]- ^ Dave Barber. A family of deltoidal hexecontahedra. 2009-12-01 [2021-08-25]. (原始内容存档于2022-03-18).
- ^ 2.0 2.1 Weisstein, Eric W. (编). Archimedean Dual Graph. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Rhombic Hexecontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Livio Zefiro. Dissection of the rhomb-icosidodecahedron in elementary regular-faced polyhedra and subsequent reassembly leading to a set of Johnson's polyhedra. Universita' di Genova. [2021-08-25]. (原始内容存档于2021-08-25).
- ^ 5.0 5.1 Catalan Solids: Deltoidal Hexecontahedron. dmccooey.com. [2021-08-25]. (原始内容存档于2022-02-14).
- ^ Koca, Mehmet and Ozdes Koca, Nazife and Koç, Ramazan. Catalan solids derived from three-dimensional-root systems and quaternions. Journal of Mathematical Physics (American Institute of Physics). 2010, 51 (4): 043501.
- ^ Weisstein, Eric W. (编). Hamiltonian Cycle. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Deltoidal hexecontahedron. fillygons.ch. [2021-08-29]. (原始内容存档于2022-03-31).
- ^ Wolfram, Stephen. "". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ 10.0 10.1 10.2 10.3 Wolfram, Stephen. "deltoidal hexecontahedron". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Wolfram, Stephen. "deltoidal hexecontahedron inradius". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Wolfram, Stephen. "zero of 820 x^4 - 5710 x^2 + 121". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Koca, Mehmet and Al-Ajmi, Mudhahir and Koç, Ramazan. Polyhedra obtained from Coxeter groups and quaternions. Journal of Mathematical Physics (American Institute of Physics). 2007, 48 (11): 113514.
- ^ 14.0 14.1 Piedade, Claudio Alexandre, How to disassemble a virus capsid: a computacional approach (PDF), 2016 [2021-09-10], (原始内容存档 (PDF)于2021-09-10)
- ^ Pieter Goetschalckx, Local Symmetry Preserving Operations on Polyhedra (PDF), [2021-09-10], (原始内容存档 (PDF)于2021-09-10)
- ^ Gábor Gévay. ICOSAHEDRAL MORPHOLOGY. WORLD SCIENTIFIC. 1992-03: 177–203 [2021-10-13]. ISBN 9789810206000. doi:10.1142/9789814439497_0012. (原始内容存档于2021-10-26) (英语).
- ^ Weisstein, Eric W. (编). Isohedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ includes d24 The Dice Lab Set of five Red unique dice d60. chilloutkitchen.com. (原始内容存档于2021-07-28).
- ^ Hong-Man Ma, Hui-Yan Zhao, Jing Wang, Ying Liu. Au 42 N 20 : A Stable Aromatic Deltoidal Hexecontahedron Molecule. The Journal of Physical Chemistry C. 2020-01-09, 124 (1): 425–429 [2021-10-13]. ISSN 1932-7447. doi:10.1021/acs.jpcc.9b08443. (原始内容存档于2021-10-29) (英语).