包络
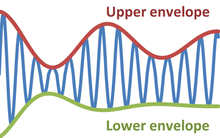
物理学和工程学中,震荡信号的包络是一条勾勒出极值的光滑曲线。[1]因此,包络将恒定振幅的概念推广为瞬时振幅。下图展示了在上包络与下包络之间振荡的调制正弦曲线。包络函数可以是时间、空间、角度或任何变量的函数。
拍频波[编辑]
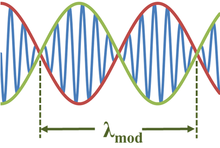
在空间x和时间t中产生包络函数的常见情况是波长和频率几乎相同的两个波的叠加:[2]
其中使用了两个正弦波相加的三角函数,以及近似值Δλ ≪ λ:
调制波长是包络波长的两倍,因为余弦波的每半个波长都控制着正弦波的正负值。同样,拍频是包络波的频率,是调制波频率的两倍,即2Δf。[4]
如果这种波是声波,耳朵听到的是与f有关的频率,振幅随拍频的变化而变化。[4]
相速度与群速度[编辑]

除2π之外,上述正弦波的参数是:
下标C、E分别指载波和包络。同样的振幅F来自相同的ξC、ξE值,在适当相关的x、t选择下,每个本身都可能返回到相同的值。这种不变性意味着可以在空间中追踪波形,并找到固定振幅的位置在时间中传播时的速度;要使载波参数保持不变,条件为:
这表明,要保持恒定振幅,距离Δx与时间间隔Δt的关系是相速度 vp
引入波向量k,可得更常见的群速度表达式:
注意到,对于微小变化Δλ而言,相应的波向量小变化Δk为:
于是群速度可重写为:
其中ω是以弧度/秒为单位的频率:ω = 2πf。在所有介质中,频率和波向量都与色散关系ω = ω(k)有关,群速度可以写成:

在经典真空等介质中,电磁波的色散关系为:
其中c0是经典真空中的光速。这种情况下,相速度和群速度都是c0。
在所谓色散介质中,色散关系可能是波向量的复杂函数,相速度和群速度也不尽相同。例如,对于GaAs中原子振动(声子)表现出的几种波,不同波向量k方向的色散关系如图所示。一般而言,相速度和群速度的方向可能不同。[7]
函数近似[编辑]

凝聚态物理学中,晶体中移动电荷载流子的能量本征函数可表为布洛赫波:
其中n是带的编号(如导带或价带),r是空间位置,k是波矢。指数是正弦变化函数,对应一个缓慢变化的包络,调制波函数un, k的快速变化部分,描述波函数在晶格原子核心附近的行为。包络只限于晶体布里渊区限定范围内的k值,这就限制了它随位置r变化的速度。
用量子力学确定载流子行为时,通常使用包络近似法。其中薛定谔方程被简化到仅指包络的行为,边界条件直接应用于包络函数,而非完整的波函数。[9]例如,被困在杂质附近的载流子波函数受包络函数F支配,函数是布洛赫函数的叠加:
其中包括F(k)的傅立叶分量由近似薛定谔方程求得。[10]在某些应用中,周期部分uk被带缘附近的值取代,如k=k0,接着:[9]
衍射图样[编辑]

多缝衍射图样的包络由单缝衍射图样决定,后者的包络线如下:[11]
其中α是衍射角,d是狭缝宽度,λ是波长。对多个狭缝,图样为[11]
其中q为狭缝数量,g是光栅常数。第一个因子即单缝结果I1,调制着第二个变化更快的因子,取决于狭缝数量与间距。
估计[编辑]
包络检波器是从信号中提取包络的电子电路。
在数字信号处理中,可用希尔伯特变换或滑动平均RMS振幅估计包络。[12]
另见[编辑]
参考文献[编辑]
- ^ C. Richard Johnson, Jr; William A. Sethares; Andrew G. Klein. Figure C.1: The envelope of a function outlines its extremes in a smooth manner. Software Receiver Design: Build Your Own Digital Communication System in Five Easy Steps. Cambridge University Press. 2011: 417. ISBN 978-0521189446.
- ^ 2.0 2.1 Blair Kinsman. Wind Waves: Their Generation and Propagation on the Ocean Surface Reprint of Prentice-Hall 1965. Courier Dover Publications. 2002: 186. ISBN 0486495116.
- ^
Mark W. Denny. Air and Water: The Biology and Physics of Life's Media
 . Princeton University Press. 1993: 289. ISBN 0691025185.
. Princeton University Press. 1993: 289. ISBN 0691025185.
- ^ 4.0 4.1 Paul Allen Tipler; Gene Mosca. Physics for Scientists and Engineers, Volume 1 6th. Macmillan. 2008: 538. ISBN 978-1429201247.
- ^ Peter W. Milonni; Joseph H. Eberly. §8.3 Group velocity. Laser Physics 2nd. John Wiley & Sons. 2010: 336. ISBN 978-0470387719.
- ^ Peter Y. Yu; Manuel Cardona. Fig. 3.2: Phonon dispersion curves in GaAs along high-symmetry axes. Fundamentals of Semiconductors: Physics and Materials Properties 4th. Springer. 2010: 111. ISBN 978-3642007095.
- ^ V. Cerveny; Vlastislav Červený. §2.2.9 Relation between the phase and group velocity vectors. Seismic Ray Theory. Cambridge University Press. 2005: 35. ISBN 0521018226.
- ^ G Bastard; JA Brum; R Ferreira. Figure 10 in Electronic States in Semiconductor Heterostructures. Henry Ehrenreich; David Turnbull (编). Solid state physics: Semiconductor Heterostructures and Nanostructures. 1991: 259. ISBN 0126077444.
- ^ 9.0 9.1 Christian Schüller. §2.4.1 Envelope function approximation (EFA). Inelastic Light Scattering of Semiconductor Nanostructures: Fundamentals And Recent Advances. Springer. 2006: 22. ISBN 3540365257.
- ^ For example, see Marco Fanciulli. §1.1 Envelope function approximation. Electron Spin Resonance and Related Phenomena in Low-Dimensional Structures. Springer. 2009: 224 ff. ISBN 978-3540793649.
- ^ 11.0 11.1 Kordt Griepenkerl. Intensity distribution for diffraction by a slit and Intensity pattern for diffraction by a grating. John W Harris; Walter Benenson; Horst Stöcker; Holger Lutz (编). Handbook of physics. Springer. 2002: 306 ff. ISBN 0387952691.
- ^ Envelope Extraction - MATLAB & Simulink. MathWorks. 2021-09-02 [2021-11-16]. (原始内容存档于2023-10-19).

![{\displaystyle {\begin{aligned}F(x,\ t)&=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]+\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]\\[6pt]&\approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{\rm {mod}}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fe1e3d85c2a7bfc6a802ea34e7bd60be82159ed)
















