五邊形鑲嵌
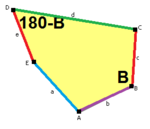
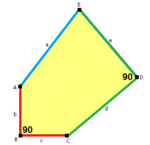
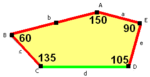
正五邊形不能鑲嵌平面，因為其內角是108°，不能整除360°。截至2015年[update]，已知有15種凸五邊形鑲嵌平面。2017年5月，里昂高等師範學校Michaël Rao宣稱已證明只存在上述的15種凸五邊形鑲嵌平面情況。[1]
歷史
[編輯]Reinhardt (1918)發現了「鑲嵌塊遞移」（tile transitive）的5種五邊形鑲嵌，即是說鑲嵌的對稱性可以將任何一塊帶到任何另一塊（用數學語言描述，鑲嵌的自同構群作用在鑲嵌塊上是可遞的。）Kershner (1968)發現了3種新的五邊形鑲嵌，都不是鑲嵌遞移的；他錯誤聲稱已經找出所有的五邊形鑲嵌。1975年Richard E. James III找到第9種。Schattschneider (1978)描述業餘數學家瑪喬里·賴斯在1976至1977年間找到新的4種五邊形鑲嵌。Schattschneider (1985)描述Rolf Stein在1985年找到的第14種五邊形鑲嵌。Bagina (2011)證明邊對邊（edge-to-edge）的凸五邊形鑲嵌只有8種，Sugimoto (2012)獨立證出同一結果。2015年，華盛頓大學數學家Casey Mann、Jennifer McLoud和David Von Derau發現了第15種五邊形鑲嵌，使用了電腦算法搜尋。[2]
五邊形的性質
[編輯]| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
 B+C=180° A+D+E=360° |
 c=e B+D=180° |
 a = b, d = c + e A = C = D = 120° |
 b = c, d = e B = D = 90° |
 a = b, d = e A = 60°, D = 120° | |
| 6 | 7 | 8 | 9 | 10 | |
 a = d = e, b = c B + D = 180°, 2B = E |
 b = c = d = e B + 2E = 2C + D = 360° |
 b = c = d = e 2B + C = D + 2E = 360° |
 b = c = d = e 2A + C = D + 2E = 360° |
 a = b = c + e A = 90°, B + E = 180°, B + 2C = 360° | |
| 11 | 12 | 13 | 14 | 15 | |
 2a + c = d = e A = 90°, 2B + C = 360° C + E = 180° |
 2a = d = c + e A = 90°, 2B + C = 360° C + E = 180° |
 d = 2a = 2e B = E = 90°, 2A + D = 360° |
 2a = 2c = d = e A = 90°, B ≈ 145.34°, C ≈ 69.32°, D ≈ 124.66°, E ≈ 110.68° (2B + C = 360°, C + E = 180°). |
 a = c = e, b = 2a A = 150°, B = 60°, C = 135°, D = 105°, E = 90° | |
參考文獻
[編輯]引用
[編輯]- ^ Exhaustive search of convex pentagons which tile the plane (PDF). [2017-07-19]. （原始內容存檔 (PDF)於2020-11-12）.
- ^ Bellos, Alex. Attack on the pentagon results in discovery of new mathematical tile. The Guardian. 11 August 2015 [2015-08-18]. （原始內容存檔於2015-08-18）.
<references>標籤中name屬性為「NPR」的參考文獻沒有在文中使用來源
[編輯]- Bagina, Olga, Tiling the plane with congruent equilateral convex pentagons, Journal of Combinatorial Theory. Series A, 2004, 105 (2): 221–232, ISSN 1096-0899, MR 2046081, doi:10.1016/j.jcta.2003.11.002
- Bagina, Olga, Мозаики из выпуклых пятиугольников [Tilings of the plane with convex pentagons], Vestnik (Kemerovo State University), 2011, 4 (48): 63–73 [29 January 2013], ISSN 2078-1768, （原始內容存檔於2015-10-01） （俄語）
- Grünbaum, Branko; Shephard, Geoffrey C., Tilings by polygons, Tilings and Patterns, New York: W. H. Freeman and Company, 1987, ISBN 0-7167-1193-1, MR 0857454
- Gardner, Martin, Tiling with Convex Polygons, Time travel and other mathematical bewilderments, New York: W. H. Freeman and Company, 1988, ISBN 0-7167-1925-8, MR 0905872
- Godrèche, C., The sphinx: a limit-periodic tiling of the plane, Journal of Physics A: Mathematical and General, 1989, 22 (24): L1163–L1166, MR 1030678, doi:10.1088/0305-4470/22/24/006
- Hirschhorn, M. D.; Hunt, D. C., Equilateral convex pentagons which tile the plane, Journal of Combinatorial Theory. Series A, 1985, 39 (1): 1–18, ISSN 1096-0899, MR 0787713, doi:10.1016/0097-3165(85)90078-0
- Kershner, Richard, On paving the plane, American Mathematical Monthly, 1968, 75: 839–844 [2015-08-18], ISSN 0002-9890, MR 0236822, doi:10.2307/2314332, （原始內容存檔於2016-03-05）
- Reinhardt, Karl, Über die Zerlegung der Ebene in Polygone, Dissertation Frankfurt a.M., Borna-Leipzig, Druck von Robert Noske, 1918 （德語）
- Schattschneider, Doris, Tiling the plane with congruent pentagons, Mathematics Magazine, 1978, 51 (1): 29–44 [2015-08-18], ISSN 0025-570X, MR 0493766, doi:10.2307/2689644, （原始內容存檔於2015-08-18）
- Schattschneider, Doris, A new pentagon tiler, Mathematics Magazine, 1985, 58 (5): 308, The cover has a picture of the new tiling
- Sugimoto, Teruhisa, Convex pentagons for edge-to-edge tiling, I. (PDF), Forma, 2012, 27 (1): 93–103 [2015-08-18], MR 3030316, （原始內容存檔 (PDF)於2015-09-24）
外部連結
[編輯]
- 埃里克·韋斯坦因. Pentagon Tiling. MathWorld.
- Pentagon Tilings（頁面存檔備份，存於網際網路檔案館）
- The 14 Pentagons that Tile the Plane（頁面存檔備份，存於網際網路檔案館）
