大地水準面高

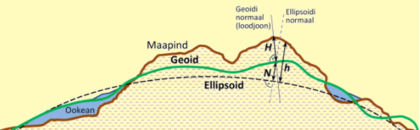
大地水準面高（N）是大地水準面（綠色實線）上一點沿法線（縱向黑色虛線）投影至參考橢球面（橫向黑色虛線）的距離

大地水準面高，也稱大地水準面起伏或大地水準面差距，指大地水準面上的一點沿法線投影至參考橢球面上的距離。當大地水準面高為正值時，表示大地水準面在參考橢球面的上方，反之則表示其在參考橢球面的下方。在正高系統中，大地水準面高亦被描述成大地高與正高的差距。

數學表達

設大地水準面有一點 $\mathbf {P}$ ，其沿法線投影到參考橢球面上的點為 $\mathbf {Q}$，則 $\mathbf {P}$ 點處的大地水準面高 $N$ 即為兩點之間的距離 。

與擾動位的關係

主條目：布隆斯公式

設 $\mathbf {P}$ 點處的擾動位為 $T$，計算得的 $\mathbf {Q}$ 點處的正常重力為 $\gamma$，則大地水準面高與前兩者的關係為：

$N={\frac {T}{\gamma }}$

該公式又被稱為布隆斯公式，由德國大地測量學家海因里希·布隆斯於1878年提出。

與垂線偏差的關係

主條目：垂線偏差

垂線偏差在南北方向（即子午圈方向）上的投影 $\xi$ 和其在東西方向（即卯酉圈方向）上的投影 $\eta$ 與大地水準面高有如下關係：

${\begin{cases}\xi =-{\frac {1}{R}}{\partial N \over \partial \varphi }\\\eta =-{\frac {1}{R\cos \varphi }}{\partial N \over \partial \lambda }\end{cases}}$

其中，$R$為地球的平均半徑，$\left(\varphi ,\lambda \right)$是 $\mathbf {Q}$ 點的地理坐標。

測定方式

斯托克斯方法

在斯托克斯提出的計算公式中，擾動位 $T$ 以整個大地水準面 $\sigma$ 上重力異常 $\Delta g$ 的積分形式表達：

$T={R \over 4\pi }\iint \limits _{\sigma }\Delta g\,S(\psi )\operatorname {d} \!\sigma$

則大地水準面高的計算公式為：

$N={R \over 4\pi {\bar {\gamma }}}\iint \limits _{\sigma }\Delta g\,S(\psi )\operatorname {d} \!\sigma$

其中的 $S(\psi )$ 被稱為斯托克斯函數，該項由單位球面上的被計算點與重力異常觀測值所在的角元素之間的夾角 $\psi$ 決定：

$S(\psi )={1 \over \sin(\psi /2)}-6\sin {\psi \over 2}+1-5\cos {\psi }-3\cos {\psi }\ln {(\sin {\psi \over 2}+\sin ^{2}{\psi \over 2})}$

地球重力場模型法

在地球重力場模型中，擾動位 $T$ 被表達成球諧函數的級數表達式：

$T={GM \over r}{\sum _{n=2}^{\infty }}{({a \over r})}^{n}{\sum _{m=0}^{n}}\left[{\bar {C}}_{nm}\cos {m\lambda }+{\bar {S}}_{nm}\sin {m\lambda }\right]{\bar {P}}_{nm}(\cos {\theta })$

通過布隆斯公式，上式可轉化為大地水準面高的計算公式：

$N={GM \over r{\bar {\gamma }}}{\sum _{n=2}^{\infty }}{({a \over r})}^{n}{\sum _{m=0}^{n}}\left[{\bar {C}}_{nm}\cos {m\lambda }+{\bar {S}}_{nm}\sin {m\lambda }\right]{\bar {P}}_{nm}(\cos {\theta })$

上式中的各個量的含義如下：

• $(r,\theta ,\lambda )$是空間中某特定點的球坐標，$r\$是點的地心距離， $\theta$和 $\lambda \$分別是點的地心緯度的餘角和經度

• $GM$ 為重力場模型的地心引力常數

• $a$ 為地球（參考橢球體）的長半軸
• ${\overline {P}}_{nm}$ 是 $n\$階 $m\$次的完全正規化締合勒讓德多項式
• ${\overline {C}}_{nm}$ 和 ${\overline {S}}_{nm}$ 是由測量數據確定的該重力場模型的完全正規化係數
• ${\bar {\gamma }}$ 是某區域內正常重力的平均值

衛星測高法

海水面大地高

衛星測高技術通過搭載在人造衛星上的測高儀來測得海水面的大地高（橢球高） $h$，其基本觀測方程為：

$h=r_{s}-\rho -r_{e}-C$

上式中各個量的含義如下：

• $r_{s}$是衛星的地心距離
• $\rho$ 是測高儀測得的衛星相對於海水面的高度
• $r_{e}$ 是衛星星下點的地心距離，該星下點位於參考橢球面上

特別地，$C$ 是因橢球法線與地心向徑的不重合而產生的改正項，量級通常在0至5米之間，計算公式為：

$C={r_{e} \over 8}\left(1-{r_{e} \over r_{s}}\right)e^{4}\sin ^{2}2B$

其中 $e$ 為參考橢球的偏心率， $B$為星下點的大地緯度。

海面地形改正

通過上述公式計算得海水面大地高 $h$ 包含海面地形 $H$ 和大地水準面高 $N$ 兩部分：

$h=N+H$

其中海面地形描述的是瞬時海平面與大地水準面之間的差距。因此，在求得海水面的大地高之後，既能研究瞬時海水面的起伏變化，也可以確定一段時間內的平均海水面與大地水準面的形態分佈。

相關條目

• 大地水準面
• 參考橢球面