同調

數學上（特別是代數拓撲和抽象代數），同調 （homology，在希臘語中homos = 同）是一類將一個可換群或者模的序列和特定數學物件（例如拓撲空間或者群）聯繫起來的過程。背景知識請參看同調論。

對於一個特定的拓撲空間，同調群通常比同倫群要容易計算得多，因此通常來講用同調來輔助空間分類要容易處理一些。

同調群的構造

其過程如下：給定物件$X$，首先定義鏈複形，它包含了$X$的資訊。一個鏈複形是一個由群同態聯繫起來的可換群或者模$A_{0},A_{1},A_{2},\dots$的序列，群同態$d_{n}:A_{n}\rightarrow A_{n-1}$滿足任何兩個相連的同態的複合為0: $d_{n}\circ d_{n+1}=0$對於所有$n$成立。這意味着第$n+1$個映射的像包含在第$n$個映射的核中，我們定義$X$的$n$階同調群為商群（商模）

$H_{n}(X)=\mathrm {ker} (d_{n})/\mathrm {im} (d_{n+1}).$

鏈複形稱為正合的，如果（$n+1$）階映射的像總是等於$n$階映射的核。因此$X$的同調群是衡量$X$所關聯的鏈複形離正合有「多遠」的障礙。

非正式的例子

非正式地，拓撲空間X的同調是X的拓撲不變量的集合，用其同調群來表示

$H_{0}(X),H_{1}(X),H_{2}(X),\ldots$

其中第$k$個同調群$H_{k}(X)$描繪了$X$中的$k$維圈 (cycle)，實現為$k+1$維圓盤邊界 (boundary) 的障礙。0維同調群刻畫了兩個零維圈，也即點，實現成一維圓盤，也即線段的邊界的障礙，因此$H_{0}(X)$刻畫了$X$中的路徑連通分支。

圓，或稱為1維球面$S^{1}$

一維球面 $S^{1}$是一個圓。它有一個連通分支和一個一維圈，但沒有更高維圈。其對應的同調群由下式給出

$H_{k}(S^{1})\cong {\begin{cases}\mathbb {Z} &k=0,1\\0&k\neq 0,1\end{cases}}$

其中$\mathbb {Z}$表示整數加群，$0$表示平凡群。$H_{1}(S^{1})\cong \mathbb {Z}$表示$S^{1}$的一階同調群為由一個元素生成的有限生成阿貝爾群，其唯一的生成元表示圓中包含的一維圈。

2維球面$S^{2}$即球的球殼，不包括球的內部。

二維球面$S^{2}$有一個連通分支，零個一維圈，一個二維圈（即球面），無更高維的圈，其對應的同調群為

$H_{k}(S^{2})\cong {\begin{cases}\mathbb {Z} &k=0,2\\0&k\neq 0,2\end{cases}}$

一般地，對$n$維球面$S^{n}$，其同調群為

$H_{k}(S^{n})\cong {\begin{cases}\mathbb {Z} &k=0,n\\0&k\neq 0,n\end{cases}}$

實心圓盤，即2維球$B^{2}$

二維實心球$B^{2}$有一個路徑連通分支，但與圓不同的是，$B^{2}$沒有一維或更高維的圈，其對應的同調群除了零階同調群$H_{0}(B^{2})\cong \mathbb {Z}$以外，其餘階的同調群均為平凡群。

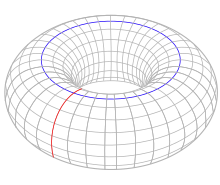環面$T=S^{1}\times S^{1}$

環面被定義為兩個圓$T^{2}=S^{1}\times S^{1}$的笛卡爾積。環面有一個路徑連通分支，兩個獨立的一維圈（在圖中以紅圈和藍圈分別標出），以及一個二維圈（環面的內部）。其對應的同調群為

$H_{k}(T^{2})\cong {\begin{cases}\mathbb {Z} &k=0,2\\\mathbb {Z} \times \mathbb {Z} &k=1\\0&k\geq 3\end{cases}}$

兩個獨立的一維圈組成了一組有限生成阿貝爾群的獨立生成元，表示為笛卡爾積群$\mathbb {Z} \times \mathbb {Z}$.

例子

引入同調的概念可以用單體複形$X$的單純同調：設$C_{n}$為$X$中的$n$維可定向單體生成的自由交換群或者模，映射$\partial _{n}:C_{n}\rightarrow C_{n+1}$映射稱為邊緣映射 (boundary map)，它將$n$維單體

$\sigma :\Delta ^{n}\rightarrow X$

映射為如下交錯和

$\sum _{i=0}^{n}(-1)^{i}\sigma |_{[e_{0},\ldots ,e_{i-1},e_{i+1},\ldots ,e_{n}]}.$

，其中$\sigma |_{[e_{0},\cdots ,e_{i-1},e_{i+1},\cdots ,e_{n}]}$表示$\sigma$限制在$e_{0},\cdots ,e_{i-1},e_{i+1},\cdots ,e_{n}$對應的面 (face)上。如果我們將模取在一個域上，則$X$的$n$階同調的維數就是$X$中$n$維圈的個數。

仿照單純同調群，可以定義任何拓撲空間$X$的奇異同調群。我們定義$X$的餘調的鏈複形中的空間為$A_{n}$為自由交換群（或者自由模），其生成元為所有從$n$為單體到$X$的連續函數。同態$d_{n}$從單體的邊緣映射得到。

同調代數中，同調用於定義導來函子，例如，Tor函子。這裏，我們可以從某個可加協變函子$F$和某個模$X$開始。$X$的鏈複形定義如下：首先找到一個自由模$F_{1}$和一個滿同態$p_{1}:F_{1}\rightarrow X$。然後找到一個自由模$F_{2}$和一個滿同態$p_{2}:F_{2}\rightarrow \mathrm {ker} (p_{1})$。以該方式繼續，得到一個自由模$F_{n}$和同態$p_{n}$的序列。將函子$F$應用於這個序列，得到一個鏈複形；這個複形的同調$H_{n}$僅依賴於$F$和$X$，並且按定義就是$F$作用於$X$的n階導來函子。

同調函子

鏈複形構成一個範疇：從鏈複形$(d_{n}:A_{n}\rightarrow A_{n-1})$到鏈複形$(e_{n}:B_{n}\rightarrow B_{n-1})$的態射是一個同態的序列$(f_{n}:A_{n}\rightarrow B_{n})$，滿足$f_{n-1}\circ d_{n}=e_{n-1}\circ f_{n}$對於所有$n$成立。$n$階同調 $H_{n}$可以視為一個從鏈複形的範疇到可換群（或者模）的範疇的協變函子。

若鏈複形以協變的方式依賴於物件$X$（也就是任何態射$X\rightarrow Y$誘導出一個從$X$的鏈複形到$Y$的鏈複形的態射），則$H_{n}$是從$X$所屬的範疇到可換群（或模）的範疇的函子。

同調和餘調的唯一區別是餘調中的鏈複形以逆變方式依賴於$X$，因此其同調群（在這個情況下稱為餘調群並記為$H^{n}$）構成從$X$所屬的範疇到可換群或者模的範疇的逆變函子。

性質

若$(d_{n}:A_{n}\rightarrow A_{n-1})$是鏈複形，滿足出有限個$A_{n}$外所有項都是零，而非零的都是有限生成可換群（或者有限維向量空間），則可以定義歐拉示性數

$\chi =\sum (-1)^{n}\,\mathrm {rank} (A_{n})$

（可換群採用階而向量空間的情況採用哈默爾維數）。事實上在同調水平上也可以計算歐拉示性數:

$\chi =\sum (-1)^{n}\,\mathrm {rank} (H_{n})$

特別地，在代數拓撲中，歐拉示性數$\chi$是拓撲空間的重要不變量。

此外，每個鏈複形的短正合序列

$0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$

誘導一個同調群的長正合序列

$\cdots \rightarrow H_{n}(A)\rightarrow H_{n}(B)\rightarrow H_{n}(C)\rightarrow H_{n-1}(A)\rightarrow H_{n-1}(B)\rightarrow H_{n-1}(C)\rightarrow H_{n-2}(A)\rightarrow \cdots \,$

這個長正合序列中的所有映射由鏈複形間的映射導出，除了映射$H_{n}(C)\rightarrow H_{n-1}(A)$之外。後者稱為連接同態，由蛇引理給出。

參看

• 奇異同調
• 餘調
• 同調論
• 同調代數

參考文獻

• Hatcher, A. Algebraic Topology. Cambridge University Press. 2002 [2021-11-18]. ISBN 0-521-79540-0. （原始內容存檔於2018-05-15）.  有仔細討論單複形、流形的同調論、奇異同調等。
• Gowers, Timothy; Barrow-Green, June; Leader, Imre (編). The Princeton Companion to Mathematics. Princeton University Press. 2010. ISBN 9781400830398. 
• Spanier, Edwin H. Algebraic Topology. Springer. 1966: 155. ISBN 0-387-90646-0.