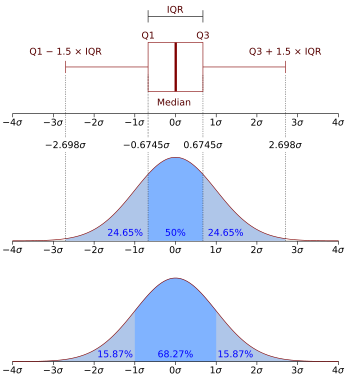
以盒状图 与概率密度函数展示的常态分布 N (0, σ 2 ) 概率密度函数 (P robability d ensity f unction,简写作PDF [ 1] 密度函数 )是描述随机变量 的输出值,在某个确定的取值点附近的可能性的函数 。图中,横轴为随机变量的取值,纵轴为概率密度函数的值,而随机变量的取值落在某个区域内的概率为概率密度函数在这个区域上的积分 。当概率密度函数存在的时候,累积分布函数 是概率密度函数的积分。概率密度函数有时也被称为概率分布函数,但这种称法可能会和累积分布函数 (CDF)或概率质量函数 (PMF)混淆。一般来说,PMF 用于离散随机变量(在可数集上取值的随机变量),而 PDF 用于连续随机变量。
对于一维实随机变量X ,设它的累积分布函数是
F
X
(
x
)
{\displaystyle F_{X}(x)}
函数
f
X
(
x
)
{\displaystyle f_{X}(x)}
∀
−
∞
<
a
<
∞
,
F
X
(
a
)
=
∫
−
∞
a
f
X
(
x
)
d
x
{\displaystyle \forall -\infty <a<\infty ,\quad F_{X}(a)=\int _{-\infty }^{a}f_{X}(x)\,dx}
那么X 是一个连续型随机变量,并且
f
X
(
x
)
{\displaystyle f_{X}(x)}
[ 2]
连续型随机变量的概率密度函数有如下性质:
∀
−
∞
<
x
<
∞
,
f
X
(
x
)
≥
0
{\displaystyle \forall -\infty <x<\infty ,\quad f_{X}(x)\geq 0}
∫
−
∞
∞
f
X
(
x
)
d
x
=
1
{\displaystyle \int _{-\infty }^{\infty }f_{X}(x)\,dx=1}
∀
−
∞
<
a
<
b
<
∞
,
P
[
a
<
X
≤
b
]
=
F
X
(
b
)
−
F
X
(
a
)
=
∫
a
b
f
X
(
x
)
d
x
{\displaystyle \forall -\infty <a<b<\infty ,\quad \mathbb {P} \left[a<X\leq b\right]=F_{X}(b)-F_{X}(a)=\int _{a}^{b}f_{X}(x)\,dx}
如果概率密度函数
f
X
(
x
)
{\displaystyle f_{X}(x)}
x
{\displaystyle x}
连续 ,那么累积分布函数可导 ,并且它的导数 :
F
X
′
(
x
)
=
f
X
(
x
)
{\displaystyle F_{X}^{\prime }(x)=f_{X}(x)}
由于随机变量X 的取值
P
[
a
<
X
≤
b
]
{\displaystyle \mathbb {P} \left[a<X\leq b\right]}
X 的概率密度函数取值不同的点只有有限个、可数无限个或者相对于整个实数轴来说测度为0(是一个零测集 ),那么这个函数也可以是X 的概率密度函数。
连续型的随机变量取值在任意一点的概率都是0。作为推论,连续型随机变量在区间上取值的概率与这个区间是开区间还是闭区间无关。要注意的是,概率
P
[
X
=
a
]
=
0
{\displaystyle \mathbb {P} \left[X=a\right]=0}
{
X
=
a
}
{\displaystyle \{X=a\}}
[ 2] 连续型均匀分布的概率密度函数 最简单的概率密度函数是均匀分布 的密度函数。对于一个取值在区间
[
a
,
b
]
{\displaystyle [a,b]}
I
[
a
,
b
]
{\displaystyle \mathbf {I} _{[a,b]}}
f
I
[
a
,
b
]
(
x
)
=
1
b
−
a
I
[
a
,
b
]
{\displaystyle f_{\mathbf {I} _{[a,b]}}(x)={\frac {1}{b-a}}\mathbf {I} _{[a,b]}}
也就是说,当x 不在区间
[
a
,
b
]
{\displaystyle [a,b]}
[
a
,
b
]
{\displaystyle [a,b]}
1
b
−
a
{\displaystyle \scriptstyle {\frac {1}{b-a}}}
常态分布的概率密度函数 常态分布 是重要的概率分布。它的概率密度函数是:
f
(
x
)
=
1
σ
2
π
e
−
(
x
−
μ
)
2
2
σ
2
{\displaystyle f(x)={1 \over \sigma {\sqrt {2\pi }}}\,e^{-{(x-\mu )^{2} \over 2\sigma ^{2}}}}
随着参数
μ
{\displaystyle \mu }
σ
{\displaystyle \sigma }
随机变量X的n阶矩 是X的n次方的期望 ,即
E
[
X
n
]
=
∫
−
∞
∞
x
n
f
X
(
x
)
d
x
{\displaystyle \mathbb {E} [X^{n}]=\int _{-\infty }^{\infty }x^{n}f_{X}(x)\,dx}
X的方差 为
σ
X
2
=
E
[
(
X
−
E
[
X
]
)
2
]
=
∫
−
∞
∞
(
x
−
E
[
X
]
)
2
f
X
(
x
)
d
x
{\displaystyle \sigma _{X}^{2}=\mathbb {E} \left[\left(X-\mathbb {E} [X]\right)^{2}\right]=\int _{-\infty }^{\infty }(x-E[X])^{2}f_{X}(x)\,dx}
更广泛的说,设
g
{\displaystyle g}
有界 连续 函数,那么随机变量
g
(
X
)
{\displaystyle g(X)}
E
[
g
(
X
)
]
=
∫
−
∞
∞
g
(
x
)
f
X
(
x
)
d
x
{\displaystyle \mathbb {E} [g(X)]=\int _{-\infty }^{\infty }g(x)f_{X}(x)\,dx}
[ 3] 对概率密度函数作类似傅里叶变换 可得特征函数 。
Φ
X
(
j
ω
)
=
∫
−
∞
∞
f
(
x
)
e
j
ω
x
d
x
{\displaystyle \Phi _{X}(j\omega )=\int _{-\infty }^{\infty }f(x)e^{j\omega x}\,dx}
特征函数与概率密度函数有一对一的关系。因此,知道一个分布的特征函数就等同于知道一个分布的概率密度函数。[ 4]








![{\displaystyle \forall -\infty <a<b<\infty ,\quad \mathbb {P} \left[a<X\leq b\right]=F_{X}(b)-F_{X}(a)=\int _{a}^{b}f_{X}(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb3a1303b46d32e29db825be059164a8974297ea)


![{\displaystyle \mathbb {P} \left[a<X\leq b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec48b2bf36f73de44d26bce27f5aaf2e4ac95c58)
![{\displaystyle \mathbb {P} \left[X=a\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3fd92f76abee82ce82f7c10533ab251f1d117b1)

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle \mathbf {I} _{[a,b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4406a0a7e0d3d39eaf3e55b86f1d3d76b315ddf1)
![{\displaystyle f_{\mathbf {I} _{[a,b]}}(x)={\frac {1}{b-a}}\mathbf {I} _{[a,b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a508f58ccb5f879a5b57fe4eac920a62011cc3fc)




![{\displaystyle \mathbb {E} [X^{n}]=\int _{-\infty }^{\infty }x^{n}f_{X}(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d29b8773308bf827f5cecd7f2bad20e67cefff)
![{\displaystyle \sigma _{X}^{2}=\mathbb {E} \left[\left(X-\mathbb {E} [X]\right)^{2}\right]=\int _{-\infty }^{\infty }(x-E[X])^{2}f_{X}(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6937db91a710b8014caaf95e225ffe2c6462b70)


![{\displaystyle \mathbb {E} [g(X)]=\int _{-\infty }^{\infty }g(x)f_{X}(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/654cf86a26b7770eda911d52c4475bddb75da02e)

