在電磁學 裏,電磁波方程式 (英語:Electromagnetic wave equation)乃是描述電磁波 傳播於介質 或真空 的二階微分方程式 。電磁波的波源是局域化的含時電荷密度 和電流密度 ,假若波源為零,則電磁波方程式約化為二階齊次微分方程式 電場
E
{\displaystyle \mathbf {E} \,\!}
磁場
B
{\displaystyle \mathbf {B} \,\!}
(
∇
2
−
1
c
2
∂
2
∂
t
2
)
E
=
0
{\displaystyle \left(\nabla ^{2}-{\frac {1}{{c}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)\mathbf {E} \ =\ 0\,\!}
(
∇
2
−
1
c
2
∂
2
∂
t
2
)
B
=
0
{\displaystyle \left(\nabla ^{2}-{\frac {1}{{c}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)\mathbf {B} \ =\ 0\,\!}
其中,
∇
2
{\displaystyle \nabla ^{2}\,\!}
拉普拉斯算符 ,
c
{\displaystyle c\,\!}
t
{\displaystyle t\,\!}
時間 。
由於光波 就是電磁波,
c
{\displaystyle c\,\!}
光速 。在真空裏,
c
=
c
0
=
299
,
792
,
458
{\displaystyle c=c_{0}=299,792,458\,\!}
自由空間 的速度。
在詹姆斯·馬克士威 的1864年論文《電磁場的動力學理論 》內,馬克士威將位移電流 與其它已成立的電磁方程式合併,因而得到了描述電磁波的波動方程式 。最令人振奮的是,這方程式所描述的波動的波速等於光波的速度。他這樣說[ 1]
這些殊途一致的結果,似乎意味著光波與電磁波都是同樣物質的屬性,並且,光波是按照著電磁定律傳播於電磁場的電磁擾動。 — 詹姆斯·馬克士威
在真空裏,馬克士威方程組 的四個微分方程式為
∇
⋅
E
=
0
{\displaystyle \nabla \cdot \mathbf {E} =0\,\!}
(1)
∇
×
E
=
−
∂
B
∂
t
{\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}\,\!}
(2)
∇
⋅
B
=
0
{\displaystyle \nabla \cdot \mathbf {B} =0\,\!}
(3)
∇
×
B
=
μ
0
ε
0
∂
E
∂
t
{\displaystyle \nabla \times \mathbf {B} =\mu _{0}\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\,\!}
(4) 其中,
μ
0
{\displaystyle \mu _{0}\,\!}
真空磁導率 ,
ε
0
{\displaystyle \varepsilon _{0}\,\!}
真空電容率 。
分別取公式(2)、(4)的旋度 ,
∇
×
(
∇
×
E
)
=
−
∂
∂
t
(
∇
×
B
)
=
−
μ
0
ε
0
∂
2
E
∂
t
2
{\displaystyle \nabla \times (\nabla \times \mathbf {E} )=-{\frac {\partial }{\partial t}}(\nabla \times \mathbf {B} )=-\mu _{0}\varepsilon _{0}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}\,\!}
∇
×
(
∇
×
B
)
=
μ
0
ε
0
∂
∂
t
(
∇
×
E
)
=
−
μ
o
ε
o
∂
2
B
∂
t
2
{\displaystyle \nabla \times (\nabla \times \mathbf {B} )=\mu _{0}\varepsilon _{0}{\frac {\partial }{\partial t}}(\nabla \times \mathbf {E} )=-\mu _{o}\varepsilon _{o}{\frac {\partial ^{2}\mathbf {B} }{\partial t^{2}}}\,\!}
應用一則向量恆等式 (這裏,
∇
2
V
{\displaystyle \nabla ^{2}\mathbf {V} }
拉普拉斯算子 ,卽拉普拉斯–德拉姆算子 )
∇
×
(
∇
×
V
)
=
∇
(
∇
⋅
V
)
−
∇
2
V
{\displaystyle \nabla \times \left(\nabla \times \mathbf {V} \right)=\nabla \left(\nabla \cdot \mathbf {V} \right)-\nabla ^{2}\mathbf {V} \,\!}
其中,
V
{\displaystyle \mathbf {V} \,\!}
將公式(1)、(3)代入,即可得到亥姆霍茲方程式 形式的波動方程式:
(
∇
2
−
1
c
2
∂
2
∂
t
2
)
E
=
0
{\displaystyle \left(\nabla ^{2}-{\frac {1}{{c}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)\mathbf {E} \ =\ 0\,\!}
(5)
(
∇
2
−
1
c
2
∂
2
∂
t
2
)
B
=
0
{\displaystyle \left(\nabla ^{2}-{\frac {1}{{c}^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)\mathbf {B} \ =\ 0\,\!}
(6) 其中,
c
=
c
0
=
1
μ
0
ε
0
=
2.99792458
×
10
8
{\displaystyle c=c_{0}={1 \over {\sqrt {\mu _{0}\varepsilon _{0}}}}=2.99792458\times 10^{8}\,\!}
電磁四維勢
A
μ
{\displaystyle A^{\mu }\,\!}
電位
ϕ
{\displaystyle \phi \,\!}
向量勢
A
{\displaystyle \mathbf {A} \,\!}
A
μ
=
d
e
f
(
ϕ
/
c
,
A
)
{\displaystyle A^{\mu }\ {\stackrel {def}{=}}\ (\phi /c,\,\mathbf {A} )\,\!}
採用勞侖次規範 :
∂
A
μ
∂
x
μ
=
0
{\displaystyle {\frac {\partial A^{\mu }}{\partial x^{\mu }}}=0\,\!}
前述那些齊次的波動方程式(5)、(6),可以按照反變形式 寫為
◻
A
μ
=
0
{\displaystyle \ \Box A^{\mu }=0\,\!}
其中,
◻
=
∂
ν
∂
ν
=
∂
2
∂
x
ν
∂
x
ν
=
1
c
2
∂
2
∂
t
2
−
∇
2
{\displaystyle \Box =\partial ^{\nu }\partial _{\nu }={\frac {\partial ^{2}}{\partial x_{\nu }\partial x^{\nu }}}={\frac {1}{{c}^{2}}}{\partial ^{2} \over \partial t^{2}}-\nabla ^{2}\,\!}
達朗貝爾算子 ,又稱為四維拉普拉斯算子 。
齊次的電磁波方程式在彎曲時空 中需要做兩處修正,分別是將偏導數替換為協變導數 ,以及增加了一項有關時空曲率的項。假設勞侖次規範 在彎曲時空中的推廣為
A
μ
;
μ
=
d
e
f
∂
A
μ
∂
x
μ
=
0
{\displaystyle {A^{\mu }}_{;\mu }\ {\stackrel {def}{=}}\ {\frac {\partial A^{\mu }}{\partial x^{\mu }}}=0\,\!}
那麼,彎曲時空中的齊次的波動方程式為
−
A
α
;
β
β
+
R
α
β
A
β
=
0
{\displaystyle -{A^{\alpha ;\beta }}_{\beta }+{R^{\alpha }}_{\beta }A^{\beta }=0\,\!}
其中,
R
α
β
{\displaystyle {R^{\alpha }}_{\beta }\,\!}
里奇曲率張量 。
追根究底,局域化的含時電荷密度 和電流密度 是電磁波的波源。在有波源的情形下,馬克士威方程組可以寫成一個非齊次的電磁波方程式的形式。正是因為波源的存在,使得偏微分方程式變為非齊次。
在齊次的電磁波方程式中,電場和磁場的每一個分量都滿足純量波動方程式
1
c
2
∂
2
f
∂
t
2
−
∇
2
f
=
0
{\displaystyle {\frac {1}{{c}^{2}}}{\partial ^{2}f \over \partial t^{2}}-\nabla ^{2}f\ =\ 0\,\!}
(7) 其中,
f
{\displaystyle f\,\!}
良態 函數,
純量波動方程式的一般解的形式為
f
(
r
,
t
)
=
g
(
k
⋅
r
−
ω
t
)
{\displaystyle f(\mathbf {r} ,t)=g(\mathbf {k} \cdot \mathbf {r} -\omega t)\,\!}
其中,
g
(
k
⋅
r
−
ω
t
)
{\displaystyle g(\mathbf {k} \cdot \mathbf {r} -\omega t)\,\!}
r
{\displaystyle \mathbf {r} \,\!}
位置向量 ,
t
{\displaystyle t\,\!}
k
{\displaystyle \mathbf {k} \,\!}
波向量 ,
ω
{\displaystyle \omega \,\!}
角頻率 。
函數
g
(
k
⋅
r
−
ω
t
)
{\displaystyle g(\mathbf {k} \cdot \mathbf {r} -\omega t)\,\!}
k
{\displaystyle \mathbf {k} \,\!}
g
(
k
⋅
r
−
ω
t
)
{\displaystyle g(\mathbf {k} \cdot \mathbf {r} -\omega t)\,\!}
波數 的色散關係 :
ω
2
=
c
2
k
2
{\displaystyle \omega ^{2}=c^{2}k^{2}\,\!}
或者,角頻率一定大於零,但波數可以是負值:
ω
=
c
|
k
|
{\displaystyle \omega =c|k|\,\!}
正弦函數 和餘弦函數 的曲線是不同相位的正弦曲線。假設,函數
g
{\displaystyle g\,\!}
正弦波 :
f
=
f
0
cos
(
k
⋅
r
−
ω
t
+
ϕ
0
)
{\displaystyle f=f_{0}\cos(\mathbf {k} \cdot \mathbf {r} -\omega t+\phi _{0})\,\!}
其中,
f
0
{\displaystyle {f}_{0}\,\!}
波幅 ,
ϕ
0
{\displaystyle \phi _{0}\,\!}
初相位 。
根據歐拉公式 ,
e
i
θ
=
cos
θ
+
i
sin
θ
{\displaystyle e^{i\theta }=\cos \theta +i\sin \theta \,\!}
函數
f
{\displaystyle f\,\!}
複數 的實值部分
f
=
Re
{
f
0
e
i
(
k
⋅
r
−
ω
t
+
ϕ
0
)
}
{\displaystyle f=\operatorname {Re} \{f_{0}e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t+\phi _{0})}\}\,\!}
以上方加有波浪號 的符號來標記複值變數 。設定複值函數
f
~
{\displaystyle {\tilde {f}}\,\!}
f
~
=
f
0
e
i
(
k
⋅
r
−
ω
t
+
ϕ
0
)
=
f
~
0
e
i
(
k
⋅
r
−
ω
t
)
{\displaystyle {\tilde {f}}=f_{0}e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t+\phi _{0})}={\tilde {f}}_{0}e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}\,\!}
其中,
f
~
0
=
f
0
e
i
ϕ
0
{\displaystyle {\tilde {f}}_{0}=f_{0}e^{i\phi _{0}}\,\!}
波幅 。
那麼,
f
=
Re
{
f
~
}
{\displaystyle f=\operatorname {Re} \{{\tilde {f}}\}\,\!}
純量波動方程式的正弦波解的形式為
f
~
{\displaystyle {\tilde {f}}\,\!}
f
{\displaystyle f\,\!}
線性方程式 ,都可以用複函數
f
~
{\displaystyle {\tilde {f}}\,\!}
f
{\displaystyle f\,\!}
由於指數函數 比三角函數 容易計算,在很多場合,都可以使用這技巧。
任意波動
f
(
r
,
t
)
{\displaystyle f(\mathbf {r} ,t)\,\!}
無限集合 的不同頻率的正弦波的線性疊加 :
f
(
r
,
t
)
=
∫
0
∞
f
~
0
(
r
,
ω
)
e
−
i
ω
t
d
ω
{\displaystyle f(\mathbf {r} ,t)=\int _{0}^{\infty }{\tilde {f}}_{0}(\mathbf {r} ,\omega )e^{-i\omega t}\ d\omega \,\!}
所以,只要能得知單獨頻率的波動
f
~
0
(
r
,
ω
)
{\displaystyle {\tilde {f}}_{0}(\mathbf {r} ,\omega )\,\!}
單色波 )的表達式,就可以求算整個波動
f
(
r
,
t
)
{\displaystyle f(\mathbf {r} ,t)\,\!}
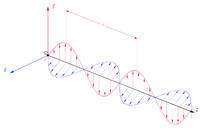
電磁波是橫波,電場方向與磁場方向相互垂直,又都垂直於傳播方向。 從前面的分析,可以猜到齊次的電磁波方程式的單色正弦平面波的解為:
E
~
(
r
,
t
)
=
E
~
0
e
i
(
k
⋅
r
−
ω
t
)
{\displaystyle {\tilde {\mathbf {E} }}(\mathbf {r} ,t)={\tilde {\mathbf {E} }}_{0}e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}\,\!}
B
~
(
r
,
t
)
=
B
~
0
e
i
(
k
⋅
r
−
ω
t
)
{\displaystyle {\tilde {\mathbf {B} }}(\mathbf {r} ,t)={\tilde {\mathbf {B} }}_{0}e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}\,\!}
其中,
E
~
0
{\displaystyle {\tilde {\mathbf {E} }}_{0}\,\!}
B
~
0
{\displaystyle {\tilde {\mathbf {B} }}_{0}\,\!}
E
~
{\displaystyle {\tilde {\mathbf {E} }}}
B
~
{\displaystyle {\tilde {\mathbf {B} }}}
振幅 向量。
這兩個方程式顯示出正弦平面波的傳播方向是
k
{\displaystyle \mathbf {k} \,\!}
k
⋅
E
~
(
r
,
t
)
=
k
⋅
E
~
0
=
0
{\displaystyle \mathbf {k} \cdot {\tilde {\mathbf {E} }}(\mathbf {r} ,t)=\mathbf {k} \cdot {\tilde {\mathbf {E} }}_{0}=0\,\!}
k
⋅
E
~
(
r
,
t
)
=
k
⋅
B
~
0
=
0
{\displaystyle \mathbf {k} \cdot {\tilde {\mathbf {E} }}(\mathbf {r} ,t)=\mathbf {k} \cdot {\tilde {\mathbf {B} }}_{0}=0\,\!}
電場和磁場垂直於波向量,波動傳播的方向。所以,電磁波是橫波 。
由於法拉第電磁感應定律 方程式(2),
∇
×
E
~
=
(
∇
e
i
(
k
⋅
r
−
ω
t
)
)
×
E
~
0
=
i
k
×
E
~
=
−
∂
B
~
∂
t
=
i
ω
B
~
{\displaystyle \nabla \times {\tilde {\mathbf {E} }}=\left(\nabla e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}\right)\times {\tilde {\mathbf {E} }}_{0}=i\mathbf {k} \times {\tilde {\mathbf {E} }}=-{\frac {\partial {\tilde {\mathbf {B} }}}{\partial t}}=i\omega {\tilde {\mathbf {B} }}\,\!}
將角頻率與波數的色散關係式
ω
=
c
k
{\displaystyle \omega =ck\,\!}
B
~
=
k
ω
×
E
~
=
1
c
k
^
×
E
~
{\displaystyle {\tilde {\mathbf {B} }}={\frac {\mathbf {k} }{\omega }}\times {\tilde {\mathbf {E} }}={\frac {1}{c}}{\hat {\mathbf {k} }}\times {\tilde {\mathbf {E} }}\,\!}
所以,電場與磁場相互垂直於對方;磁場的大小等於電場的大小除以光速。
電磁波譜 顯示出不同種類的電磁波的頻率值域和波長值域。可見光譜只佔有寬廣的電磁波譜的一小部分。由於馬克士威方程組在真空裡的線性性質,其解答可以分解為一集合的正弦波。將這集合的正弦波的疊加在一起,又可以形成原本的解答。這是傅立葉變換 方法解析微分方程式的基礎概念。電磁波方程式的正弦波解的形式為
E
(
r
,
t
)
=
E
0
cos
(
ω
t
−
k
⋅
r
+
ϕ
0
)
{\displaystyle \mathbf {E} (\mathbf {r} ,t)=\mathbf {E} _{0}\cos(\omega t-\mathbf {k} \cdot \mathbf {r} +\phi _{0})\,\!}
B
(
r
,
t
)
=
B
0
cos
(
ω
t
−
k
⋅
r
+
ϕ
0
)
{\displaystyle \mathbf {B} (\mathbf {r} ,t)=\mathbf {B} _{0}\cos(\omega t-\mathbf {k} \cdot \mathbf {r} +\phi _{0})\,\!}
波向量與角頻率的關係為
k
=
|
k
|
=
ω
c
=
2
π
λ
{\displaystyle k=|\mathbf {k} |={\omega \over c}={2\pi \over \lambda }\,\!}
其中,
λ
{\displaystyle \lambda \,\!}
波長 。
按照波長長短,從長波開始,電磁波可以分類為電能 、無線電波 、微波 、紅外線 、可見光 、紫外線 、X-射線 和伽馬射線 等等。普通實驗使用的光譜儀 就足以分析從2 奈米 到2500 奈米波長的電磁波。使用這種儀器,可以得知物體、氣體或甚至恆星的詳細物理性質。這是天文物理學 的必備儀器。例如,氫原子 會發射波長為21.12公分的無線電波。
原柱對稱形共軸傳輸線 如圖右,思考一條由半徑為
a
{\displaystyle a\,\!}
b
{\displaystyle b\,\!}
共軸傳輸線 。假設這傳輸線與z-軸平行。由於共軸傳輸線的內部有一條直導線,不是空心的,它可以傳輸
E
z
=
0
{\displaystyle E_{z}=0\,\!}
B
z
=
0
{\displaystyle B_{z}=0\,\!}
圓柱坐標
(
s
,
ϕ
,
z
)
{\displaystyle (s,\phi ,z)\,\!}
[ 2]
E
(
r
,
t
)
=
E
0
s
cos
(
k
z
−
ω
t
)
s
^
{\displaystyle {\mathbf {E} }(\mathbf {r} ,t)={\frac {{\mathbf {E} }_{0}}{s}}\cos(kz-\omega t){\hat {s}}\,\!}
B
(
r
,
t
)
=
E
0
c
s
cos
(
k
z
−
ω
t
)
ϕ
^
{\displaystyle {\mathbf {B} }(\mathbf {r} ,t)={\frac {\mathbf {E} _{0}}{cs}}\cos(kz-\omega t){\hat {\phi }}\,\!}
這一組方程式顯示出電磁波方程式的圓柱對稱性解的一種形式。
思考一個位於原點 的振盪中的磁偶極矩
m
=
m
0
cos
(
ω
t
)
{\displaystyle m=m_{0}\cos(\omega t)\,\!}
球坐標
(
r
,
θ
,
ϕ
)
{\displaystyle (r,\theta ,\phi )\,\!}
r
{\displaystyle \mathbf {r} \,\!}
[ 2]
E
(
r
,
t
)
=
E
0
sin
θ
r
[
cos
(
k
r
−
ω
t
)
−
1
k
r
[
sin
(
k
r
−
ω
t
)
]
ϕ
^
{\displaystyle {\mathbf {E} }(\mathbf {r} ,t)={\frac {\mathbf {E} _{0}\sin \theta }{r}}\left[\cos(kr-\omega t)-{\frac {1}{kr}}[\sin(kr-\omega t)\right]{\hat {\phi }}\,\!}
B
(
r
,
t
)
=
−
E
0
sin
θ
c
r
[
cos
(
k
r
−
ω
t
)
−
1
k
r
[
sin
(
k
r
−
ω
t
)
]
θ
^
{\displaystyle {\mathbf {B} }(\mathbf {r} ,t)=-{\frac {\mathbf {E} _{0}\sin \theta }{cr}}\left[\cos(kr-\omega t)-{\frac {1}{kr}}[\sin(kr-\omega t)\right]{\hat {\theta }}\,\!}
這是一組滿足電磁波方程式的球面波方程式。
Tipler, Paul. Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.) . W. H. Freeman. 2004. ISBN 0-7167-0810-8 Jackson, John D. Classical Electrodynamics (3rd ed.). Wiley. 1998. ISBN 0-471-30932-X Landau, L. D., The Classical Theory of Fields (Course of Theoretical Physics: Volume 2), (Butterworth-Heinemann: Oxford, 1987). ISBN 0-08-018176-7 .
Maxwell, James C. A Treatise on Electricity and Magnetism . Dover. 1954. ISBN 0-486-60637-6
















































































![{\displaystyle {\mathbf {E} }(\mathbf {r} ,t)={\frac {\mathbf {E} _{0}\sin \theta }{r}}\left[\cos(kr-\omega t)-{\frac {1}{kr}}[\sin(kr-\omega t)\right]{\hat {\phi }}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e418be3f8cb788b42fe000542b47a59516685d1f)
![{\displaystyle {\mathbf {B} }(\mathbf {r} ,t)=-{\frac {\mathbf {E} _{0}\sin \theta }{cr}}\left[\cos(kr-\omega t)-{\frac {1}{kr}}[\sin(kr-\omega t)\right]{\hat {\theta }}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e0ad50c26ae352b32d3cec6958bccf9591c89b8)