旋度

一架农业飞机尾部激起的气流。烟雾成顺时针或逆时针方向运动，对应的旋度在飞机前行的方向上。

旋度是向量分析中的一个向量算子，可以表示三维向量场对某一点附近的微元造成的旋转程度。 这个向量提供了向量场在这一点的旋转性质。旋度向量的方向表示向量场在这一点附近旋转度最大的环量的旋转轴，它和向量旋转的方向满足右手定则。旋度向量的大小则是绕着这个旋转轴旋转的环量，也是这一点附近旋转度最大的环量。举例来说，假设一台滚筒洗衣机运行的时候，从前方看来，内部的水流是逆时针旋转，那么中心水流速度向量场的旋度就是朝前方向外的向量。

定义

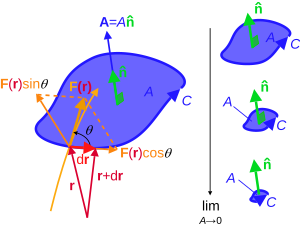
定义向量场的旋度，首先要引入环量（或称为旋涡量）的概念。给定一个三维空间中的向量场$\mathbf{A}$以及一个简单闭合有向曲线$\Gamma$，$\mathbf{A}$沿着曲线$\Gamma$的环量就是$\mathbf{A}$沿着路径$\Gamma$的闭合曲线积分：

$\operatorname{Circ}_{\mathbf{A}}( \Gamma ) =\oint_{\Gamma}\mathbf{A}\cdot\mathrm{d} \boldsymbol{l}$

其中$\mathrm{d} \boldsymbol{l}$是曲线$\Gamma$上的线元，方向是曲线的切线方向，其正方向规定为使得闭合曲线$\Gamma$所包围的面积在它的左侧。举例来说，假如在河岸边看到河中有逆时针旋转的漩涡，那么在漩涡范围内，水流围绕涡心旋转，所以水流速度$\boldsymbol{v}$沿着逆时针围绕漩涡的闭合曲线积分一定大于零，即是说环量大于零。这说明漩涡中的水流流速场在漩涡范围内是转圈旋转的。

环量和通量一样，是描述向量场的重要参数。某个区域中的环量不等于零，说明这个区域中的向量场表现出环绕某一点或某一区域旋转的特性。旋度则是局部地描述这一特性的方法。为了描述一个向量场$\mathbf{A}$在一点附近的环量，将闭合曲线$\Gamma$收小，使它包围的面元$\Delta S$的面积$\left | \Delta S \right \vert$趋于零。向量场$\mathbf{A}$沿着$\Gamma$的环量和面元$\Delta S$的比值在$\left | \Delta S \right \vert$趋于零时候的极限值：

$\lim_{\Delta S \to 0 } \frac{1}{\left | \Delta S \right \vert} \oint_{\Gamma}\mathbf{A}\cdot\mathrm{d} \boldsymbol{l}$

就是$\mathbf{A}$的环量面密度（或称为环量强度）。显然，随着面积$\Delta S$取的方向不同，得到的环量面密度也有大有小。如果要表现一点附近向量场的旋转程度，则应该表现出其最大可能值以及其所在面积的方向。而向量场的旋度是一个向量。它在一个方向上的投影的大小表示了在这个方向上的环量面密度的大小。也就是说，$\mathbf{A}$在一点的旋度记为$\operatorname{curl} \mathbf{A}(x)$或$\operatorname{rot} \mathbf{A}(x)$，满足：

$\operatorname{curl} \mathbf{A}(x)\cdot \mathbf{n} = \lim_{ \Delta S_{\mathbf{n}} \to 0 } \frac{1}{\left | \Delta S_{\mathbf{n}} \right \vert} \oint_{\Gamma}\mathbf{A}\cdot\mathrm{d} \boldsymbol{l}$

如果用Nabla算子$\nabla$表示的话，向量场$\mathbf{A}$的旋度记作：$\operatorname{curl}\,\mathbf{A} = \nabla \times \mathbf{A} .$ 从定义中可以看出，旋度是向量场的一种强度性质，就如同密度、浓度、温度一样，它对应的广延性质是向量场沿一个闭合曲线的环量。如果一个向量场中处处的旋度都是零，则称这个场为无旋场或保守场。

分量表示

在不同的坐标系下，向量场的旋度有不同的表达方式。

直角坐标系

在三维直角坐标系Oxyz中，设向量场$\mathbf{A}$为：

$\mathbf{A}(x,y,z)=P(x,y,z)\mathbf{i}+Q(x,y,z)\mathbf{j}+R(x,y,z)\mathbf{k}$，

其中的$\mathbf{i}, \mathbf{j} , \mathbf{k}$分别是x轴、y轴、z轴方向上的单位向量，场的分量P、Q、R具有一阶连续偏导数， 那么在各个坐标上的投影分别为：

$\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z}$，$\frac{\partial P}{\partial z} - \frac{\partial R}{\partial x}$，$\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}$

的向量叫做向量场A的旋度，也就是：

$\operatorname{curl} \ \mathbf{A}=\nabla\times\mathbf{A}=\left(\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z}\right)\mathbf{i}+\left(\frac{\partial P}{\partial z} - \frac{\partial R}{\partial x}\right)\mathbf{j}+\left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right)\mathbf{k}$

旋度的表达式可以用也行列式记号形式表示：

$\operatorname{curl}\ \mathbf{A}= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac {\partial}{\partial z} \\ P & Q & R \end{vmatrix}$

需要注意的是这里的行列式记号只有形式上的意义，因为真正的行列式中的系数应该是数而不是$\mathbf{i},\mathbf{j}, \mathbf{k}$这样的向量。这种表示方法只是便于记忆旋度在直角坐标系中的表达式。

圆柱坐标系

圆柱坐标系中，假设物体的位置为$(r, \theta, z)$，定义其径向单位矢量、横向单位矢量和纵向单位矢量为$\boldsymbol{e}_{r}, \boldsymbol{e}_{\theta}, \boldsymbol{e}_{z}$，那么向量场$\mathbf A$可以表示成：

$\mathbf A = A_r(r, \theta, z) \boldsymbol{e}_{r} + A_z(r, \theta, z) \boldsymbol{e}_{z} + A_{\theta}(r, \theta, z)\boldsymbol{e}_{\theta},$

向量场A的旋度就是：

$\operatorname{curl}\, \mathbf A = \left(\frac1r \frac{\partial A_z}{\partial \theta} - \frac{\partial A_{\theta}}{\partial z} \right) \boldsymbol{e}_{r} + \left( \frac{\partial A_r}{\partial z} - \frac{\partial A_{z}}{\partial r} \right)\boldsymbol{e}_{\theta} + \frac1r \left( \frac{\partial (rA_{\theta})}{\partial r} - \frac{\partial A_{r}}{\partial \theta} \right)\boldsymbol{e}_{z} \, .$

旋度的表达式可以用也行列式记号形式表示（即向量积的行列式形式）：

$\nabla\times\mathbf{A}= \begin{vmatrix} \mathbf{e}_{r} & \mathbf{e}_{\theta} & \mathbf{e}_z \\ \frac{\partial}{\partial r} & \frac{1}{r}\frac{\partial}{\partial \theta} & \frac {\partial}{\partial z} \\ A_r & A_{\theta} & A_z \end{vmatrix}$

球坐标系

球坐标系中，假设物体的位置用球坐标表示为$(r , \theta , \varphi )$，定义它的基矢：$\boldsymbol{e}_{r}, \boldsymbol{e}_{\theta}, \boldsymbol{e}_{\varphi}$，则向量场A可以表示成：

$\mathbf A = A_r (r , \theta , \varphi ) \boldsymbol{e}_{r} + A_{\theta} (r , \theta , \varphi ) \boldsymbol{e}_{\theta} + A_{ \varphi } (r , \theta , \varphi ) \boldsymbol{e}_{\varphi } ,$

向量场A的旋度就是：

$\operatorname{curl}\, \mathbf A = \frac1{r \sin\theta} \left( \frac{\partial (A_{\varphi}\sin\theta )}{\partial \theta} - \frac{\partial A_{\theta}}{\partial \varphi} \right) \boldsymbol{e}_{r} + \frac1r \left( \frac1{ \sin\theta}\frac{\partial A_r}{\partial \varphi } - \frac{\partial (r A_{ \varphi })}{\partial r} \right)\boldsymbol{e}_{\theta} + \frac1r \left( \frac{\partial (rA_{\theta})}{\partial r} - \frac{\partial A_{r}}{\partial \theta} \right)\boldsymbol{e}_{ \varphi } \, .$

旋度的表达式可以用也行列式记号形式表示（即向量积的行列式形式）：

$\nabla\times\mathbf{A}= \begin{vmatrix} \mathbf{e}_{r} & \mathbf{e}_{\theta} & \mathbf{e}_{\varphi} \\ \frac{\partial}{\partial r} & \frac{1}{r}\frac{\partial}{\partial \theta} & \frac {1}{r\sin\theta}\frac {\partial}{\partial \varphi} \\ A_r & A_{\theta} & A_{\varphi} \end{vmatrix}$

例子

图1

下面是两个简单的例子，用以说明旋度的直观意义。第一个例子是向量场$\mathbf{F}_1$(如右图1）：

$\mathbf{F}_1(x,y,z)=y\boldsymbol{\hat{x}}-x\boldsymbol{\hat{y}}.$

直观上，可以看出向量场$\mathbf{F}_1$是表示一个向顺时针方向旋转的趋势。假如在图中放一个点，它会被向量场“推动”，沿顺时针方向绕圈运动。根据右手定则，旋度的方向应该是朝向页面内。按照右手系坐标的方向，旋度的方向是z轴的负方向。而经过计算可以得出，向量场$\mathbf{F}_1$的旋度

${\nabla} \times \mathbf{F}_1=0\boldsymbol{\hat{x}}+0\boldsymbol{\hat{y}}+ \left[{\frac{\partial}{\partial x}}(-x) -{\frac{\partial}{\partial y}} y\right]\boldsymbol{\hat{z}}=-2\boldsymbol{\hat{z}}$

图2

和直观的推断相符合。以上的计算表明，旋度是一个恒定的量：$-2\boldsymbol{\hat{z}}$。也就是说，每一点上旋转的程度都是一样的。旋度图象为右图2：

图3

图4

第二个例子是向量场$\mathbf{F}_2$(如右图3）：

$\mathbf{F}_2(x,y,z)=-x^2\boldsymbol{\hat{y}}.$

向量场$\mathbf{F}_2$的作用是向下，越是靠近两侧，向下的趋势越显著。假想这个向量场是一个力场，一块薄板水平放在图的右边，那么由于更靠右的地方受到向下的力更大，薄板会顺时针转动。类似地，如果将薄板水平放在图的左边，则会逆时针转动。所以$\mathbf{F}_2$的旋转作用是右侧顺时针、左侧逆时针，而且越偏离中心，作用越大。按照右手定则，旋度应该是右侧朝z轴负方向（指向页面内），左侧朝z轴正方向（指向页面外）。实际的计算可以得到：

${\nabla} \times \mathbf{F}_2 =0\boldsymbol{\hat{x}}+0\boldsymbol{\hat{y}}+ {\frac{\partial}{\partial x}}(-x^2) \boldsymbol{\hat{z}}=-2x\boldsymbol{\hat{z}}.$

所以$x>0$时是朝z轴负方向，$x<0$时是朝z轴正方向，和直观推断相符合。旋度图象为右图4。

性质

以下的性质都可以从常见的求导法则推出。最重要的是，旋度是一个线性算子，也就是说：

$\operatorname{curl} \, ( a\mathbf{F} + b\mathbf{G} ) = a\;\operatorname{curl} \, ( \mathbf{F} ) + b\;\operatorname{curl} \, ( \mathbf{G} )$

其中F和G是向量场，a和b是实数。

设$\varphi$是标量函数，F是向量场，则它们的乘积的旋度为：

$\operatorname{curl} \, (\varphi \mathbf{F}) = \operatorname{grad}(\varphi) \times \mathbf{F} + \varphi \;\operatorname{curl}\,(\mathbf{F}),$

或

$\nabla\times (\varphi \mathbf{F}) = (\nabla\varphi) \times \mathbf{F} + \varphi \;\nabla \times \mathbf{F}.$

设有两个向量场F和G，则它们的向量积的旋度为：

$\nabla\times (\mathbf{F}\times\mathbf{G}) = (\mathbf{G}\cdot\nabla )\mathbf{F} \;-\; (\nabla\cdot \mathbf{F})\mathbf{G}-(\mathbf{F}\cdot\nabla)\mathbf{G} +(\nabla\cdot \mathbf{G} ) \mathbf{F}$

一个标量场f的梯度场是无旋场，也就是说它的旋度处处为零：$\nabla\times (\nabla f) = 0.$

一个向量场F的旋度场是无源场，也就是说它的散度处处为零：$\nabla\cdot (\nabla \times \mathbf{F} ) = 0.$

F的旋度场的旋度场则是：$\nabla \times (\nabla \times \mathbf{F} ) = \nabla(\nabla\cdot \mathbf{F}) - \nabla^2 \mathbf{F} .$

旋度的斯托克斯公式

三维空间ℝ³中，设Γ为分段光滑的空间有向闭曲线，S是以$\Gamma=\partial S$为边界的分片光滑的有向曲面，Γ的正向与S的侧符合右手规则，函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在曲面S（连同边界Γ）上具有一阶连续偏导数，则有

$\iint\limits_{S}(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z})dydz+(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x})dzdx+(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy=\oint\limits_{\Gamma}Pdx+Qdy+Rdz$

用旋度表示，就是：

$\int_{S} (\nabla \times \mathbf{A}) \cdot d\mathbf{S} = \oint_{\partial S} \mathbf{A} \cdot \mathrm{d} \boldsymbol{l}$

这个公式是一般的斯托克斯公式（在n=2时）的特例，在欧氏3维空间上的向量场的旋度的曲面积分和向量场在曲面边界上的线积分之间建立了联系。具体就是，向量场A在某个曲面的封闭边界线上的闭合路径积分，等于A的旋度场在这个曲面上的积分。

历史

作为向量分析的基础概念，旋度同样源自对四元数上的微积分研究。哈密尔顿在介绍四元数的运算时，将一个四元数$q = A+B\boldsymbol{i}+C\boldsymbol{j}+D\boldsymbol{k}$中的$A$称为“标量部分”，将$B\boldsymbol{i}+C\boldsymbol{j}+D\boldsymbol{k}$称为“向量部分”。他引入了四元数的偏微分算子$\nabla = \boldsymbol{i}\frac{\mathrm{d}}{\mathrm{d}x}+ \boldsymbol{j} \frac{\mathrm{d}}{\mathrm{d}y} + \boldsymbol{k} \frac{\mathrm{d}}{\mathrm{d}z}$（即$\nabla$算子）后，计算$\nabla$对一个四元数之向量部分$\sigma = B\boldsymbol{i}+C\boldsymbol{j}+D\boldsymbol{k}$的效果：

$\nabla \sigma = (\boldsymbol{i}\frac{\mathrm{d}}{\mathrm{d}x}+ \boldsymbol{j} \frac{\mathrm{d}}{\mathrm{d}y} + \boldsymbol{k} \frac{\mathrm{d}}{\mathrm{d}z})( B\boldsymbol{i}+C\boldsymbol{j}+D\boldsymbol{k})$

$= -\left(\frac{\mathrm{d}B}{\mathrm{d}x}+ \frac{\mathrm{d}C}{\mathrm{d}y}+\frac{\mathrm{d}D}{\mathrm{d}z} \right) +\left( \left(\frac{\mathrm{d}D}{\mathrm{d}y} - \frac{\mathrm{d} C}{\mathrm{d} z}\right)\boldsymbol{i}+\left(\frac{\mathrm{d}B}{\mathrm{d}z} - \frac{\mathrm{d}D}{\mathrm{d} x}\right)\boldsymbol{j}+\left(\frac{\mathrm{d}C}{\mathrm{d}x} - \frac{\mathrm{d}B}{\mathrm{d}y}\right)\boldsymbol{k}\right)$

麦克斯韦在1873年的论文中将其中的“标量部分”：$-\left(\frac{\mathrm{d}B}{\mathrm{d}x}+ \frac{\mathrm{d}C}{\mathrm{d}y}+ \frac{\mathrm{d}D}{\mathrm{d}z}\right)$称为“聚集度”（Convergence），而将“向量部分”：$\left( \frac{\mathrm{d}D}{\mathrm{d}y} - \frac{\mathrm{d} C}{\mathrm{d} z}\right)\boldsymbol{i}+\left(\frac{\mathrm{d}B}{\mathrm{d}z} - \frac{\mathrm{d}D}{\mathrm{d} x}\right)\boldsymbol{j}+\left(\frac{\mathrm{d}C}{\mathrm{d}x} - \frac{\mathrm{d}B}{\mathrm{d}y}\right)\boldsymbol{k}$称为“旋度”（Curl）或“变度”（Version）。他在写给泰特的信中解释了他起名“旋度”前的想法。他最初想将这一部分称为“扭曲度”（Twist），但可能会被理解为“旋扭”（screw）或“螺旋”（helix）；而他想表达的概念是类似“转”（turn）或“变动”（version）。他曾想用“拧动”（Twirl）一词，但又认为它太过“活泼”（racy），对于数学家来说动感过于强烈，所以最后使用了“旋度”。海维赛德在1883年发表的论文：《电学与磁学中的若干关系》（Some Electrostatic and Magnetic Relations）中讨论了$\nabla$算子对一个四元数$q$的作用效果。他认为有必要将$\nabla q$的三个部分分开，将$\nabla q$的向量部分分成散度部分$\operatorname{div}\, q$和旋度部分$\operatorname{curl}\, q$。

参见

• 散度
• 涡量
• 偏导数
• 向量恆等式列表