微分学

| 系列條目 |
| 微积分学 |
|---|
 |
微分学(英語:Differential calculus)是微積分学的一部份,是通过导数和微分来研究曲线斜率、加速度、最大值和最小值的一门学科,也是探討特定數量變化速率的學科。微分学是微積分的二個主要分支之一[註 1][1]。
微分学主要研究的主題是函數的導數、相關的標示方式(例如微分)以及其應用。函數在特定點的導數可以說明函數在此輸入值附近的變化率。尋找導數的過程即為微分。若以圖示表示,函數在某一點的微分是函数图形在那一點的切線斜率(前提是在那一點的導數存在而且有定義)。針對單實數變數的實值函數而言,函數在某一點的導數也就可以決定在那一點最佳的线性近似。微分和積分的關係可以由微积分基本定理來說明,此定理說明微分是積分的逆運算。
幾乎所有量化的學科中都有微分的應用。例如在物理学中,運動物體其位移對時間的導數即為其速度,速度對時間的導數就是加速度、物體动量對時間的導數即為物體所受的力,重新整理後可以得到牛顿第二运动定律。化学反应的化學反應速率也是導數。在運籌學中,會透過導數決定在運輸或是設計上最有效率的作法。
導數常用來找函數的极值。含有微分項的方程式稱為微分方程,是自然現象描述的基礎。微分以及其廣義概念出現在許多數學領域中,例如複分析、泛函分析、微分几何、测度及抽象代数。
導數[编辑]
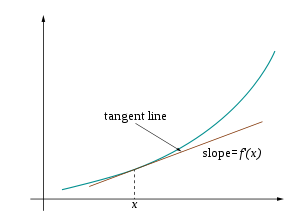

假設和y是實數,而且y是x的函數,也就是說,針對每一個x,都有一個對應的y。兩者的關係可以表示為y = f(x)。若f(x)是直線的方程式(稱為一次方程),則會存在兩個實數m和b使得y = mx + b。在這個「斜率-截距式」中,m是斜率,可以用下式來求得:
其中符號Δ(是希臘大寫字母Δ)表示「變化」。以下的式子會成立:Δy = m Δx.
一般的函數不是直線,因此沒有斜率。在幾何上來看,函數f在x = a的導數就是函數f在a點切線的斜率(如圖)。常會表示為f ′(a) 或dy/dx|x = a。因為導數是f在a點線性近似的斜率,因此導數(以及函數f在a點的值)是函數f在a點附近最佳的線性化近似。
若在函數f定義域中的每一點a都有導數,則存在一函數可以將每一點a對應到函數f在a點的導數。例如,若函數f(x) = x2,則其導數函數f ′(x) = dy/dx = 2x。
另一個有關的表示法是函數的微分。若x和y是實數變數,函數f在x點的導數為函數f在x點切線的斜率。因為f的引數及輸出都是純量,因此f的導數也是實數。若x和y是向量,則f圖形的最佳線性近似會和函數f在不同方向的變化有關。找到在單一方向的最佳近似,也就決定了偏微分,一般會表示為∂y/∂x。若找到了函數f在所有方向的線性化近似,則稱為全微分。
微分的歷史[编辑]
若以切線來看,微分的概念很早以前就出現了,像希臘幾何學家欧几里得(約300 BC)、阿基米德(約287–212 BC)及阿波罗尼奥斯(約262–190 BC)[2]。阿基米德也引進了無窮小量的使用,不過最早是用在面積及體積上的研究,而不是在導數及切線上,參考阿基米德使用的無窮小量。
在印度數學家的研究中有看到用無窮小量來探討量的變化,最早也許可以推到西元500年,當時天文學家及數學家阿耶波多用無窮小量來研究月球軌道[3]。在印度數學家婆什迦羅第二(1114–1185)時,用無窮小量來計算量變化的研究有顯著的進展,也有人提到[4]在他的著作中已提到許多微分学的重要概念,例如罗尔定理[5]。
伊斯蘭數學家納色阿爾圖斯(1135年–1213年)在其著作《Treatise on Equations》中說明了部份三次方程有解的條件,是透過找適當三次多項式的最大值來求得。他證明了三次多項式 a x2 — x3的最大值出現在x = 2a/3,並且得到結論:方程式 a x2 — x3 = c在c = 4 a3/27時恰有一正值的解,若0 < c < 4 a3/27會有二個正值的解[6]。科學歷史學家Roshdi Rashed[7]認為阿爾圖斯一定是用到了三次多項式的導數才得到此一結果。不過也有其他學者質疑Rashed的想法,他們認為Rashed也可能用了其他不用導數概念的作法[6]。
普遍認為近代微積分的發展是因為艾萨克·牛顿(1643年–1727年)及戈特弗里德·莱布尼茨(1646年–1716年)同時但獨立個別的研究[8],並且整合了有關微分及導數的作法。不過其中關鍵的概念(也是後來認定微積分是由他們兩人創始的原因)是結合微分以及積分的微积分基本定理[9],這也讓以往計算面積及體積,自從海什木(Alhazen)以來沒有大幅進步的的方式變的過時[10]。有關牛顿和莱布尼茨在微分上的想法,都是以早期數學家的貢獻為基礎,例如皮埃爾·德·費馬(1607年-1665年)、伊萨克·巴罗(1630年–1677年)、勒内·笛卡尔(1596年–1650年)、克里斯蒂安·惠更斯(1629年–1695年)、布莱兹·帕斯卡(1623年–1662年)及約翰·沃利斯 (1616年–1703年)。有關費馬的影響,牛頓曾在一封信中提到:「我從費馬畫切線的方式得到有關(通量)方法的暗示,將其用在抽象的方程……,我擴展了這個概念(directly and invertedly, I made it general.)[11]。一般會將導數早期的發展歸功於伊萨克·巴罗[12],不過牛頓和莱布尼茨仍在微分學的歷史上有重要的貢獻,其中也包括了牛頓將微分用在理论物理学中,而莱布尼茨發展的符號到現今仍在普遍使用。
自從17世紀起,許多數學家都對微分学有所貢獻。在19世紀時,在奧古斯丁·路易·柯西(1789年–1857年)、波恩哈德·黎曼(1826年–1866年)及卡尔·魏尔斯特拉斯(1815年–1897年)等數學家的貢獻下,微分學已更加的嚴謹。微分學也在此一時期擴展到欧几里得空间及复平面。
微分的應用[编辑]
最佳化[编辑]
若f是在ℝ(或是其他開區間)內的可微函数,而x是f有局部最小值或是局部最大值的位置,則f在x處的導數為零。滿足f'(x) = 0的點稱為臨界點或是驻点(則f在x處的值稱為臨界值)。若f沒有處處可微的特性,則f不可微的點也稱為臨界點。
若f是二次可微,則f的臨界點x可以用f在x的二次導數來分析:
- 若二次導數為正,則x是局部最小值
- 若二次導數為負,則x是局部最大值
- 若二次導數為零,則x可能是局部最小值、是局部最大值,也可能都不是(例如,f(x) = x3在x = 0處為臨界點,但不是局部最小值也不是局部最大值,而 f(x) = ± x4在x = 0處為臨界點,分別是局部最小值及局部最大值)
上述作法稱為二次導數測試。一次導數測試是另一種分析方式,考慮f'在臨界點前後的符號變化。
取導數,並且求解臨界點是要找局部最小值或最大值的最簡單作法,常應用在最优化中。根據极值定理,連續函數在閉區間內至少會有一次局部最小值及局部最大值。若函數可微,其局部最小值及局部最大值只會出現在臨界點或是端點上。
取局部最小值及局部最大值也可以在函數圖形的繪制上:只要找到可微分函數的局部最小值、局部最大值以及位,可以根據觀察函數在各臨界點之間的趨勢來繪制簡圖。
在高維度的空間中,标量函數的臨界點是其梯度為0的點。仍然可以用二次導數測試來分析臨界點,作法是考慮函數在臨界點上二階導數形成海森矩阵的特征值。若所有特徵值都為正,此點為局部最小值;若所有特徵值都為負,此點為局部最大值;若部份為正,部份為負,表示臨界點為鞍點;不過若有部份特徵值為零,則無法以此方式判斷。
變分法[编辑]
最佳化問題的一個例子是:找到在一曲面上,通過曲面上二點的最短路徑。若是在平面上,其最短路徑是直線。不過若曲面是較複雜的形狀(例如蛋形),最短路问题的解就不是那麼直觀了,此路徑稱為测地线,而這也是最佳化問題中最簡單的問題之一。另一個例子是:找到可以填充空間中封閉曲線的最小面積曲面,此曲面稱為极小曲面,也可以透過變分法求得。
物理[编辑]
微分在物理學上格外重要:許多物理的現象都是用有關微分的方程式來描述,這類方程稱為微分方程。物理學格外關注物理量隨時間的變化,而时间导数是物理量隨時間的變化率,是許多重要概念精準定義的基礎。尤其在牛頓力學中,很重視一物體位置的时间导数:
例如:若物體在一直線上的位置可以用下式表示
則其速度為
而加速度為
此時加速度已為定值。
微分方程[编辑]
微分方程是指一函數和其微分之間的關係。常微分方程會描述單變數函數和其微分之間的關係。而偏微分方程則是多變數函數和其偏微分之間的關係。在自然科學、數學建模,甚至是數學領域中都常常會出現微分方程。例如,牛頓第二定律描述力和加速度的關係,可以表示為以下的常微分方程
一維空間下的熱傳導方程式描述熱在一桿狀物上如何傳遞,其偏微分方程如下
此處u(x,t)為桿狀物時間t時,在位置x的溫度,而α為一常數,和熱在桿狀物上傳遞的速度成正比。
均值定理[编辑]

均值定理提供了函數的導數和其原始值之間的關係。若f(x)是實值函數,而a 和b是實數,且a < b,則根據均值定理(配合少許的假設),兩點(a, f(a))和(b, f(b))之間的斜率會等於在a和b中間某一點c的切線斜率。換句話說
實際上,均值定理是以其導數的方式來控制一個函數。例如,假設f有導數,在每一點均為0,這表示其每一點的切線都是水平線,因此其函數應該也就是水平線。均值定理證明這是對的:f圖上二點之間的斜率必須等於f中的某一條切線。而所有的切線斜率都是0,因此從函數上任二點之的直線斜率也是0。這表示函數不會上昇也不會下降,因此是水平線。若是導數的條件比較複雜,所產生的原函數資訊會比較不準確,但仍然有用。
泰勒多項式及泰勒級數[编辑]
一函數的某一點的微分是對該點附近最佳的線性近似,不過這和實際的函數可能有很大的差異。改善近似的一個方式就是進行二次近似。也就是說,實值函數f(x)在x0點的線性化是線性多項式a + b(x − x0),若考慮一個二次多項式a + b(x − x0) + c(x − x0)2,可能會有更好的近似結果。若二次多項式改為三次多項式a + b(x − x0) + c(x − x0)2 + d(x − x0)3,近似效果會更好一些,此概念可以擴展到任意多次的高次多項式。針對一個多項式,都應該會有一個最佳的係數a、b、c、d……的組合,讓近似的效果最好。
在x0的邻域,對a來說,最理想的數值一定是f(x0),對b來說,最理想的數值一定是f'(x0),對For c、d及更高階的係數來說,其係數最理想的數值是由f更高階的導數決定。c最理想的數值一定是f''(x0)/2,and d最理想的數值一定是f'''(x0)/3!。利用這些係數,可以得到f的泰勒多項式。d次的泰勒多項式是對f可以有最佳近似的d次多項式,其係數可以用上述公式推廣而得。泰勒公式提供近似程度的精確範圍。若函數f是次數小於等於d的多項式。則此函數的d次泰勒多項式即為函數f。
泰勒多項式的極限是無窮級數,稱為泰勒级数。多半來說泰勒级数是原函數非常理想的近似。一函數若都各點等於其泰勒级数,稱為解析函数。若函數有不連續點或是斜率不連續的尖角,此函數不會是解析函数,不過相反的,存在一些函數是光滑函数(無窮階可導的函數),卻不是解析函数(非解析的光滑函數)。
隐函数定理[编辑]
有些幾何圖形(例如圆)無法用函数图形來表示。例如若f(x, y) = x2 + y2 − 1,其圓即為所有使f(x, y) = 0的點 (x, y)的集合。這個集合稱為f的零集。這和f本身的圖形(抛物面)不同。隐函数定理可以將f(x, y) = 0之類的關係轉換為函數。其中提到,若f是連續可微函數,f的零集中大部份都可以表示為函數圖形「粘貼」的組合。零集上的個點是否滿足上述條件,可以用一個和f微分有關的方式來確認。例如圓可以表示成二個函數圖形±「粘貼」後的結果。圓上除了(−1, 0)和(1, 0)二點之外,在其餘每一個點的鄰域上,上述二個函數中都有一個的圖形和圓的圖形類似。(上述二個函數其實剛好也通過(−1, 0)和(1, 0),不過這不是隐函数定理中提到的內容)
隐函数定理和反函数定理有密切的關係。反函数定理提到一函數在一點的開區域內具有反函數的充分條件。
注释[编辑]
参见[编辑]
參考資料[编辑]
- ^ "Integral Calculus - Definition of Integral calculus by Merriam-Webster". www.merriam-webster.com. [2018-05-01]. (原始内容存档于2021-11-22) (英语).
- ^ ,可參考《几何原本》、阿基米德重寫本及約翰·J·奧康納; 埃德蒙·F·羅伯遜, Apollonius of Perga, MacTutor数学史档案 (英语)
- ^ 約翰·J·奧康納; 埃德蒙·F·羅伯遜, Aryabhata the Elder, MacTutor数学史档案 (英语)
- ^ Ian G. Pearce. Bhaskaracharya II. (页面存档备份,存于互联网档案馆)
- ^ Broadbent, T. A. A.; Kline, M. Reviewed work(s): The History of Ancient Indian Mathematics by C. N. Srinivasiengar. The Mathematical Gazette. October 1968, 52 (381): 307–8. JSTOR 3614212. doi:10.2307/3614212.
- ^ 6.0 6.1 J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), pp. 304-309.
- ^ Cited by J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), pp. 304-309.
- ^ 牛顿在1666年開始此研究,莱布尼茨在1676年開始。但是莱布尼茨在1684年發表第一篇相關的論文,在牛頓1693年的第一篇論文之前。有可能莱布尼茨看過牛頓在1673年或1676年研究的草稿,也有可能是牛頓用了莱布尼茨的研究來改進他自己的論文。最後造成了牛顿和莱布尼茨在微積分上的爭議,內容就是誰才是第一個創建微積分的人,這造成18世紀初期的數學家群體中的震撼
- ^ 此定理限制較多的版本以往已由詹姆斯·格雷果里(1638年–1675年),而皮埃爾·德·費馬(1601年–1665)的著作中也有提到一些關鍵的例子,不過這仍是具有紀念性的成就
- ^ Victor J. Katz (1995), "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3): 163-174 [165-9 & 173-4]
- ^ Sabra, A I. Theories of Light: From Descartes to Newton. Cambridge University Press. 1981: 144. ISBN 978-0521284363.
- ^ Eves, H. (1990).
- J. Edwards. Differential Calculus. London: MacMillan and Co. 1892 [2018-07-18]. (原始内容存档于2019-05-21).
|









![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)




