旋度

曲線積分的向量方向約定，可用右手定則從向量場的旋轉方向去確定它的旋度向量方向，旋度向量${\hat {n}}$對應右手拇指的指向，向量場$A$的旋轉方向${\hat {\omega }}$對應右手彎曲的其他四指的指向。

在向量分析中，旋度（英語：curl）是一個向量算子，表示在三維歐幾里德空間中的向量場的無窮小量旋轉。在向量場每個點上，點的旋度表示為一個向量，稱為旋度向量。這個向量的特性（長度和方向）刻畫了在這個點上的旋轉。

旋度的方向是旋轉的軸，它由右手定則來確定，而旋度的大小是旋轉的量。如果向量場表示一個移動的流形的流速，則旋度是這個流形的環量面密度。旋度為零的向量場叫做無旋向量場。旋度是向量的一種微分形式。微積分基本定理的對應形式是開爾文-斯托克斯定理，它將向量場旋度的曲面積分關聯於這個向量場環繞邊界曲線的曲線積分。

對於旋度curl F還經常使用可替代的術語迴轉度（rotation或rotational）和可替代的符號rot F和∇ × F。前者特別用於很多歐洲國家，後者使用del（或稱nabla）算子和叉積，更多用於其它國家。

不同於梯度和散度，旋度不能簡單的推廣到其他維度；某些推廣是可能的，但是只有在三維中，在幾何上定義的向量場旋度還是向量場。這個現象類似於三維叉積，這個聯繫反應在旋度的符號∇ ×上。

旋度的名稱「curl」最初由詹姆斯·克拉克·麥克斯韋在1871年提出，但這個概念顯然最初用於James MacCullagh在1839年對光學場理論的構建中。

定義

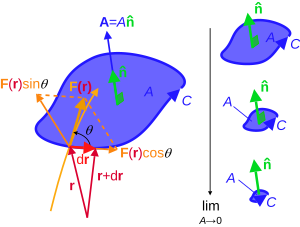
F在位置r上的分量，平面上閉合曲線C的法線和切線，這個曲線圍成的向量面積 A = An̂。

定義向量場的旋度，首先要引入環量（或稱為旋渦量）的概念。給定一個三維空間中的向量場$\mathbf {A}$以及一個簡單閉合有向曲線$\Gamma$，$\mathbf {A}$沿着曲線$\Gamma$的環量就是$\mathbf {A}$沿着路徑$\Gamma$的閉合曲線積分：

$\operatorname {Circ} _{\mathbf {A} }(\Gamma )=\oint _{\Gamma }\mathbf {A} \cdot \mathrm {d} {\boldsymbol {l}}$

其中$\mathrm {d} {\boldsymbol {l}}$是曲線$\Gamma$上的線元，方向是曲線的切線方向，其正方向規定為使得閉合曲線$\Gamma$所包圍的面積在它的左側。舉例來說，假如在河岸邊看到河中有逆時針旋轉的漩渦，那麼在漩渦範圍內，水流圍繞渦心旋轉，所以水流速度${\boldsymbol {v}}$沿着逆時針圍繞漩渦的閉合曲線積分一定大於零，即是說環量大於零。這說明漩渦中的水流流速場在漩渦範圍內是轉圈旋轉的。

環量和通量一樣，是描述向量場的重要參數。某個區域中的環量不等於零，說明這個區域中的向量場表現出環繞某一點或某一區域旋轉的特性。旋度則是局部地描述這一特性的方法。為了描述一個向量場$\mathbf {A}$在一點附近的環量，選擇包括這一點的一個微小面元$\Delta S$，考慮向量場$\mathbf {A}$沿其邊界曲線$\Gamma$的環量。當面元$\Delta S$收小，面積$\left|\Delta S\right\vert$趨於零的時候，向量場$\mathbf {A}$沿着$\Gamma$的環量和面元$\Delta S$面積的比值的極限值：

$\lim _{\Delta S\to 0}{\frac {1}{\left|\Delta S\right\vert }}\oint _{\Gamma }\mathbf {A} \cdot \mathrm {d} {\boldsymbol {l}}$

稱作$\mathbf {A}$的環量面密度（或稱為環量強度）。顯然，隨着面元$\Delta S$選取的方向不同，得到的環量面密度也有大有小。如果要表現一點附近向量場的旋轉程度，則應該表現出其最大可能值以及對應面元選取的方向。而向量場的旋度是一個向量。它在一個方向上的投影的大小表示了在這個方向上的環量面密度的大小。也就是說，$\mathbf {A}$在一點的旋度記為$\mathbf {curl\,} \mathbf {A} (x)$或$\mathbf {rot\,} \mathbf {A} (x)$，滿足：

$\mathbf {curl\,} \mathbf {A} (x)\cdot \mathbf {n} =\lim _{\Delta S_{\mathbf {n} }\to 0}{\frac {1}{\left|\Delta S_{\mathbf {n} }\right\vert }}\oint _{\Gamma _{\mathbf {n} }}\mathbf {A} \cdot \mathrm {d} {\boldsymbol {l}}$

其中的$\Delta S_{\mathbf {n} }$指以單位向量$\mathbf {n}$為法向量的面元，$\Gamma _{\mathbf {n} }$指它的邊界曲線。如果用Nabla算子${\boldsymbol {\nabla }}$表示的話，向量場$\mathbf {A}$的旋度記作：$\mathbf {curl\,} \mathbf {A} ={\boldsymbol {\nabla }}\times \mathbf {A} .$ 從定義中可以看出，旋度是向量場的一種強度性質，就如同密度、濃度、溫度一樣，它對應的廣延性質是向量場沿一個閉合曲線的環量，所以說旋度是環量的面密度。如果一個向量場中處處的旋度都是零，則稱這個場為無旋場或保守場。

分量表示

在不同的坐標系下，向量場的旋度有不同的表達方式。

直角坐標系

在三維直角坐標系 $xyz$ 中，設向量場 $\mathbf {A}$ 為：

$\mathbf {A} (x,y,z)=A_{x}(x,y,z)\mathbf {i} +A_{y}(x,y,z)\mathbf {j} +A_{z}(x,y,z)\mathbf {k}$，

其中的 $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$ 分別是 $x$軸、$y$軸、$z$軸方向上的單位向量，場的分量 $A_{x},A_{y},A_{z}$ 具有一階連續偏導數， 那麼在各個坐標上的投影分別為：

${\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}},\quad {\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}},\quad {\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}$

的向量叫做向量場A的旋度，也就是：

$\mathbf {curl\,} \ \mathbf {A} ={\boldsymbol {\nabla }}\times \mathbf {A} =\left({\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}\right)\mathbf {k}$

旋度的表達式也可以用行列式記號形式表示：

$\mathbf {curl\,} \mathbf {A} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\A_{x}&A_{y}&A_{z}\end{vmatrix}}$

需要注意的是這裏的行列式記號只有形式上的意義，因為真正的行列式中的系數應該是數值而不是 $\mathbf {i} ,\mathbf {j} ,\mathbf {k}$ 這樣的向量。這種表示方法只是便於記憶旋度在直角坐標系中的表達式。

圓柱坐標系

圓柱坐標系中，假設物體的位置為$(\rho ,\varphi ,z)$，定義其徑向單位向量、橫向單位向量和縱向單位向量為${\boldsymbol {e}}_{\rho },{\boldsymbol {e}}_{\varphi },{\boldsymbol {e}}_{z}$，那麼向量場$\mathbf {A}$可以表示成：

$\mathbf {A} =A_{\rho }(\rho ,\varphi ,z){\boldsymbol {e}}_{\rho }+A_{\varphi }(\rho ,\varphi ,z){\boldsymbol {e}}_{\varphi }+A_{z}(\rho ,\varphi ,z){\boldsymbol {e}}_{z}$，

向量場A的旋度就是：

$\mathbf {curl\,} \mathbf {A} =\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right){\boldsymbol {e}}_{\rho }+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\boldsymbol {e}}_{\varphi }+{\frac {1}{\rho }}\left({\frac {\partial ({\rho }A_{\varphi })}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\boldsymbol {e}}_{z}$。

旋度的表達式也可以用行列式記號形式表示（即向量積的行列式形式），比如：

${\boldsymbol {\nabla }}\times \mathbf {A} ={\begin{vmatrix}{\frac {1}{\rho }}\mathbf {e} _{\rho }&\mathbf {e} _{\varphi }&{\frac {1}{\rho }}\mathbf {e} _{z}\\{\frac {\partial }{\partial \rho }}&{\frac {\partial }{\partial \varphi }}&{\frac {\partial }{\partial z}}\\A_{\rho }&\rho A_{\varphi }&A_{z}\end{vmatrix}}$

要注意的是：以上的行列式中元素並不是可交換的。實際計算時，展開式其中的每一項應該是第一列的元素乘以第二列的元素再作用於第三列的元素。例如應該是${\frac {1}{\rho }}\mathbf {e} _{z}\cdot {\frac {\partial }{\partial \rho }}(\rho A_{\varphi })$而不是${\frac {\partial }{\partial \rho }}(\rho A_{\varphi }\cdot {\frac {1}{\rho }}\mathbf {e} _{z}).$ 後文中的球面坐標系表達式也是如此。

球坐標系

球坐標系中，假設物體的位置用球坐標表示為$(r,\theta ,\varphi )$，定義它的單位向量：${\boldsymbol {e}}_{r},{\boldsymbol {e}}_{\theta },{\boldsymbol {e}}_{\varphi }$，則向量場A可以表示成：

$\mathbf {A} =A_{r}(r,\theta ,\varphi ){\boldsymbol {e}}_{r}+A_{\theta }(r,\theta ,\varphi ){\boldsymbol {e}}_{\theta }+A_{\varphi }(r,\theta ,\varphi ){\boldsymbol {e}}_{\varphi },$

向量場A的旋度就是：

$\mathbf {curl\,} \mathbf {A} ={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\varphi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \varphi }}\right){\boldsymbol {e}}_{r}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {\partial (rA_{\varphi })}{\partial r}}\right){\boldsymbol {e}}_{\theta }+{\frac {1}{r}}\left({\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {\partial A_{r}}{\partial \theta }}\right){\boldsymbol {e}}_{\varphi }\,.$

旋度的表達式也可以用行列式記號形式表示（即向量積的行列式形式）：

${\boldsymbol {\nabla }}\times \mathbf {A} ={\frac {1}{r^{2}\sin \theta }}{\begin{vmatrix}\mathbf {e} _{r}&r\mathbf {e} _{\theta }&r\sin \theta \mathbf {e} _{\varphi }\\{\frac {\partial }{\partial r}}&{\frac {\partial }{\partial \theta }}&{\frac {\partial }{\partial \varphi }}\\A_{r}&rA_{\theta }&r\sin \theta A_{\varphi }\end{vmatrix}}$

例子

圖1

下面是兩個簡單的例子，用以說明旋度的直觀意義。第一個例子是向量場$\mathbf {F} _{1}$（如右圖1）：

$\mathbf {F} _{1}(x,y,z)=y{\boldsymbol {\hat {x}}}-x{\boldsymbol {\hat {y}}}.$

直觀上，可以看出向量場$\mathbf {F} _{1}$是表示一個向順時針方向旋轉的趨勢。假如在圖中放一個點，它會被向量場「推動」，沿順時針方向繞圈運動。根據右手定則，旋度的方向應該是朝向頁面內。按照右手系坐標的方向，旋度的方向是z軸的負方向。而經過計算可以得出，向量場$\mathbf {F} _{1}$的旋度

${\boldsymbol {\nabla }}\times \mathbf {F} _{1}=0{\boldsymbol {\hat {x}}}+0{\boldsymbol {\hat {y}}}+\left[{\frac {\partial }{\partial x}}(-x)-{\frac {\partial }{\partial y}}y\right]{\boldsymbol {\hat {z}}}=-2{\boldsymbol {\hat {z}}}$

圖2

和直觀的推斷相符合。以上的計算表明，旋度是一個恆定的量：$-2{\boldsymbol {\hat {z}}}$。也就是說，每一點上旋轉的程度都是一樣的。旋度圖象為右圖2：

圖3

圖4

第二個例子是向量場$\mathbf {F} _{2}$（如右圖3）：

$\mathbf {F} _{2}(x,y,z)=-x^{2}{\boldsymbol {\hat {y}}}.$

向量場$\mathbf {F} _{2}$的作用是向下，越是靠近兩側，向下的趨勢越顯著。假想這個向量場是一個力場，一塊薄板水平放在圖的右邊，那麼由於更靠右的地方受到向下的力更大，薄板會順時針轉動。類似地，如果將薄板水平放在圖的左邊，則會逆時針轉動。所以$\mathbf {F} _{2}$的旋轉作用是右側順時針、左側逆時針，而且越偏離中心，作用越大。按照右手定則，旋度應該是右側朝z軸負方向（指向頁面內），左側朝z軸正方向（指向頁面外）。實際的計算可以得到：

${\boldsymbol {\nabla }}\times \mathbf {F} _{2}=0{\boldsymbol {\hat {x}}}+0{\boldsymbol {\hat {y}}}+{\frac {\partial }{\partial x}}(-x^{2}){\boldsymbol {\hat {z}}}=-2x{\boldsymbol {\hat {z}}}.$

所以$x>0$時是朝z軸負方向，$x<0$時是朝z軸正方向，和直觀推斷相符合。旋度圖象為右圖4。

性質

以下的性質都可以從常見的求導法則推出。最重要的是，旋度是一個線性算子，也就是說：

$\mathbf {curl\,} (a\mathbf {F} +b\mathbf {G} )=a\;\mathbf {curl\,} (\mathbf {F} )+b\;\mathbf {curl\,} (\mathbf {G} )$

其中F和G是向量場，a和b是實數。

設$\varphi$是純量函數，F是向量場，則它們的乘積的旋度為：

$\mathbf {curl\,} (\varphi \mathbf {F} )=\mathbf {grad\,} (\varphi )\times \mathbf {F} +\varphi \;\mathbf {curl\,} (\mathbf {F} ),$

或

${\boldsymbol {\nabla }}\times (\varphi \mathbf {F} )=({\boldsymbol {\nabla }}\varphi )\times \mathbf {F} +\varphi \;{\boldsymbol {\nabla }}\times \mathbf {F} .$

設有兩個向量場F和G，則它們的向量積的旋度為：

${\boldsymbol {\nabla }}\times (\mathbf {F} \times \mathbf {G} )=(\mathbf {G} \cdot {\boldsymbol {\nabla }})\mathbf {F} \;-\;({\boldsymbol {\nabla }}\cdot \mathbf {F} )\mathbf {G} -(\mathbf {F} \cdot {\boldsymbol {\nabla }})\mathbf {G} +({\boldsymbol {\nabla }}\cdot \mathbf {G} )\mathbf {F}$

一個純量場 $f$ 的梯度場是無旋場，也就是說它的旋度處處為零：${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}f)=0.$

一個向量場 $\mathbf {F}$ 的旋度場是無源場，也就是說 ${\boldsymbol {\nabla }}\times \mathbf {F}$ 的散度處處為零：${\boldsymbol {\nabla }}\cdot ({\boldsymbol {\nabla }}\times \mathbf {F} )=0.$

F 的旋度場的旋度場則有公式：${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times \mathbf {F} )={\boldsymbol {\nabla }}({\boldsymbol {\nabla }}\cdot \mathbf {F} )-\nabla ^{2}\mathbf {F} .$

旋度的斯托克斯公式

主條目：斯托克斯定理

三維空間 $\mathbb {R} ^{3}$ 中，設 $\Gamma$ 為分段光滑的空間有向閉曲線， $S$ 是以 $\Gamma =\partial S$ 為邊界的分片光滑的有向曲面，$\Gamma$ 的正向與 $S$ 的側符合右手規則，函數 $P(x,y,z),Q(x,y,z),R(x,y,z)$ 在曲面 $S$（連同邊界 $\Gamma$ 上具有一階連續偏導數，則有

$\iint \limits _{S}\left({\frac {\partial R}{\partial y}}-{\frac {\partial Q}{\partial z}}\right)\mathrm {d} y\,\mathrm {d} z+\left({\frac {\partial P}{\partial z}}-{\frac {\partial R}{\partial x}}\right)\mathrm {d} z\,\mathrm {d} x+\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)\mathrm {d} x\,\mathrm {d} y=\oint \limits _{\Gamma }P\mathrm {d} x+Q\mathrm {d} y+R\mathrm {d} z$

用旋度表示，就是：

$\int _{S}({\boldsymbol {\nabla }}\times \mathbf {A} )\cdot \mathrm {d} \mathbf {S} =\oint _{\partial S}\mathbf {A} \cdot \mathrm {d} \mathbf {l}$

這個公式是一般的斯托克斯公式（在n=2時）的特例，在歐氏3維空間上的向量場的旋度的曲面積分和向量場在曲面邊界上的線積分之間建立了聯繫。具體就是，向量場A在某個曲面的封閉邊界線上的閉合路徑積分，等於A的旋度場在這個曲面上的積分。

歷史

作為向量分析的基礎概念，旋度同樣源自對四元數上的微積分研究。哈密爾頓在介紹四元數的運算時，將一個四元數$q=A+B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}}$中的$A$稱為「純量部分」，將$B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}}$稱為「向量部分」。他引入了四元數的偏微分算子${\boldsymbol {\nabla }}={\boldsymbol {i}}{\frac {\mathrm {d} }{\mathrm {d} x}}+{\boldsymbol {j}}{\frac {\mathrm {d} }{\mathrm {d} y}}+{\boldsymbol {k}}{\frac {\mathrm {d} }{\mathrm {d} z}}$（即${\boldsymbol {\nabla }}$算子）後，計算${\boldsymbol {\nabla }}$對一個四元數之向量部分$\sigma =B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}}$的效果：

${\boldsymbol {\nabla }}\sigma =({\boldsymbol {i}}{\frac {\mathrm {d} }{\mathrm {d} x}}+{\boldsymbol {j}}{\frac {\mathrm {d} }{\mathrm {d} y}}+{\boldsymbol {k}}{\frac {\mathrm {d} }{\mathrm {d} z}})(B{\boldsymbol {i}}+C{\boldsymbol {j}}+D{\boldsymbol {k}})$

$=-\left({\frac {\mathrm {d} B}{\mathrm {d} x}}+{\frac {\mathrm {d} C}{\mathrm {d} y}}+{\frac {\mathrm {d} D}{\mathrm {d} z}}\right)+\left(\left({\frac {\mathrm {d} D}{\mathrm {d} y}}-{\frac {\mathrm {d} C}{\mathrm {d} z}}\right){\boldsymbol {i}}+\left({\frac {\mathrm {d} B}{\mathrm {d} z}}-{\frac {\mathrm {d} D}{\mathrm {d} x}}\right){\boldsymbol {j}}+\left({\frac {\mathrm {d} C}{\mathrm {d} x}}-{\frac {\mathrm {d} B}{\mathrm {d} y}}\right){\boldsymbol {k}}\right)$

麥克斯韋在1873年的論文中將其中的「純量部分」：$-\left({\frac {\mathrm {d} B}{\mathrm {d} x}}+{\frac {\mathrm {d} C}{\mathrm {d} y}}+{\frac {\mathrm {d} D}{\mathrm {d} z}}\right)$稱為「聚集度」（Convergence），而將「向量部分」：$\left({\frac {\mathrm {d} D}{\mathrm {d} y}}-{\frac {\mathrm {d} C}{\mathrm {d} z}}\right){\boldsymbol {i}}+\left({\frac {\mathrm {d} B}{\mathrm {d} z}}-{\frac {\mathrm {d} D}{\mathrm {d} x}}\right){\boldsymbol {j}}+\left({\frac {\mathrm {d} C}{\mathrm {d} x}}-{\frac {\mathrm {d} B}{\mathrm {d} y}}\right){\boldsymbol {k}}$稱為「旋度」（Curl）或「變度」（Version）。他在寫給泰特的信中解釋了他起名「旋度」前的想法。他最初想將這一部分稱為「扭曲度」（Twist），但可能會被理解為「旋扭」（screw）或「螺旋」（helix）；而他想表達的概念是類似「轉」（turn）或「變動」（version）。他曾想用「擰動」（Twirl）一詞，但又認為它太過「活潑」（racy），對於數學家來說動感過於強烈，所以最後使用了「旋度」。海維賽德在1883年發表的論文：《電學與磁學中的若干關係》（Some Electrostatic and Magnetic Relations）中討論了${\boldsymbol {\nabla }}$算子對一個四元數$q$的作用效果。他認為有必要將${\boldsymbol {\nabla }}q$的三個部分分開，將${\boldsymbol {\nabla }}$算子對$q$的向量部分作用的結果分成散度部分$\operatorname {div} \,q$和旋度部分$\mathbf {curl\,} q$。

參見

• 散度
• 渦量
• 偏導數
• 在圓柱和球坐標系中的del
• 向量恆等式列表