希爾伯特轉換

希爾伯特轉換結果（紅色）與原來的訊號——方波（藍色）

在數學與訊號處理的領域中，一個實數值函數$s(t)\,$的希爾伯特轉換(Hilbert transform)——在此標示為${\mathcal {H}}$——是將訊號$s(t)\,$與$1/(\pi t)\,$做卷積，以得到${\widehat {s}}(t)$。因此，希爾伯特轉換結果${\widehat {s}}(t)$可以被解讀為輸入是$s(t)\,$的线性非時變系统(linear time invariant system)的輸出，而此一系統的脈衝響應為$1/(\pi t)\,$。這是一項有用的數學，用在描述一個以實數值載波做調變的訊號之複數包絡(complex envelope)，出現在通訊理論（應用方面的詳述請見下文。）

希爾伯特轉換是以著名數學家大衛·希爾伯特(David Hilbert)來命名。

希爾伯特轉換表格

訊號 $u(t)\,$	希爾伯特轉換 $H(u)(t)$
$\sin(t)$	$-\cos(t)$
$\cos(t)$	$\sin(t)\,$
$\exp \left(it\right)$	$-i\exp \left(it\right)$
$\exp \left(-it\right)$	$i\exp \left(-it\right)$
$1 \over t^{2}+1$	$t \over t^{2}+1$
Sinc函数 $\sin(t) \over t$	$1-\cos(t) \over t$
矩形函数 $\sqcap (t)$	${1 \over \pi }\log \left|{t+{1 \over 2} \over t-{1 \over 2}}\right|$
狄拉克δ函数 $\delta (t)\,$	${1 \over \pi t}$
指示函数 $\chi _{[a,b]}(t)\,$	${\frac {1}{\pi }}\log \left\vert {\frac {t-a}{t-b}}\right\vert$

Notes

常數之希爾伯特轉換為零

定義

希爾伯特轉換定義如下：

${\widehat {s}}(t)={\mathcal {H}}\{s\}=h(t)*s(t)=\int _{-\infty }^{\infty }s(\tau )h(t-\tau )d\tau ={\frac {1}{\pi }}\int _{-\infty }^{\infty }{\frac {s(\tau )}{t-\tau }}\,d\tau .\,$

其中

$h(t)={\frac {1}{\pi t}}\,$

並考慮此積分為柯西主值(Cauchy principal value)，其避免掉在$\tau =t\,$以及$\tau =\pm \infty \,$等處的奇點。

另外要指出的是：

若$s\in L^{p}(\mathbb {R} )$，則${\mathcal {H}}(s)$可被定義，且屬於$L^{p}(\mathbb {R} )$；其中$1<p<\infty$。

参见：Lp空間

頻率響應

希爾伯特轉換之頻率響應由傅立葉變換給出：

$H(\omega )={\mathcal {F}}\{h\}(\omega )\,=-i\cdot \operatorname {sgn}(\omega )$,  

其中

• ${\mathcal {F}}$是傅立葉變換，
• i (有時寫作j )是虛數單位，
• $\omega \,$是角頻率，以及
• $\operatorname {sgn}(\omega )={\begin{cases}\ \ 1,&{\mbox{for }}\omega >0,\\\ \ 0,&{\mbox{for }}\omega =0,\\-1,&{\mbox{for }}\omega <0,\end{cases}}$

即為符号函数。

既然：

${\mathcal {F}}\{{\widehat {s}}\}(\omega )=H(\omega )\cdot {\mathcal {F}}\{s\}(\omega )$,

希爾伯特轉換會將負頻率成分$s(t)\,$偏移+90°，而正頻率成分偏移−90°。

反（逆）希爾伯特轉換

我們也注意到：$H^{2}(\omega )=-1\,$。因此將上面方程式乘上$-H(\omega )\,$，可得到：

${\mathcal {F}}\{s\}(\omega )=-H(\omega )\cdot {\mathcal {F}}\{{\widehat {s}}\}(\omega )$

從中，可以看出反（逆）希爾伯特轉換

$s(t)=-(h*{\widehat {s}})(t)=-{\mathcal {H}}\{{\widehat {s}}\}(t).\,$

特性

邊界

若 1<p<∞，則 L^p(R)之希爾伯特轉換為一有界算子，表示存在一常數C_p使得

$\|Hu\|_{p}\leq C_{p}\|u\|_{p}$

對所有 u∈L^p(R)。這個定理由Riesz (1928，VII)所推得；請一併參見Titchmarsh (1948，Theorem 101)。 最佳常數C_p可由下列算式得到:

$C_{p}={\begin{cases}\tan {\frac {\pi }{2p}}&{\text{for }}1<p\leq 2\\\cot {\frac {\pi }{2p}}&{\text{for }}2<p<\infty \end{cases}}$

這個結果由（Pichorides 1972）所推得；請一併參見Grafakos (2004，Remark 4.1.8)。上述最佳常數計算方式應用在週期性希爾伯特轉換一樣成立。

希爾伯特轉換的邊界指的是 L^p(R) 對稱級數運算子對於在 L^p(R) 之中 f 的收斂

$S_{R}f=\int _{-R}^{R}{\hat {f}}({\xi })e^{2\pi ix\xi }\,d\xi$

請參見（Duoandikoetxea 2000，p.59）。

反自伴性

希爾伯特轉換為一反自伴算子，連結 L^p(R) 與其對偶空間 L^q(R)，其中 p 和 q 為 赫爾德共軛且 1 < p,q < ∞. 以符號表示

$\langle Hu,v\rangle =\langle u,-Hv\rangle$

對 u ∈ L^p(R) 且 v ∈ L^q(R) （Titchmarsh 1948，Theorem 102）.

逆轉換

希爾伯特轉換為一反-對合 （Titchmarsh 1948，p.120），意即

$H(H(u))=-u$

假定每一轉換皆完整定義過。由於 H 保存了 L^p(R)空間，這特別代表希爾伯特轉換在 L^p(R) 上是不可逆的，且

$H^{-1}=-H$

微分

正式上，一個式子其希爾伯特轉換的微分即為其微分的希爾伯特轉換，意即這兩者是可以交換的線性算子

$H\left({\frac {du}{dt}}\right)={\frac {d}{dt}}H(u)$

此一特性亦可迭代

$H\left({\frac {d^{k}u}{dt^{k}}}\right)={\frac {d^{k}}{dt^{k}}}H(u)$

給定 u 以及其前k次微分皆屬於L^p(R) （Pandey 1996，§3.3）空間，此項論述為嚴格成立。在頻域上可以輕易驗證這件事情，由於微分在頻域上即為與 ω 之乘積。

旋積

希爾伯特轉換可表示為與一調節分布之旋積 （Duistermaat & Kolk 2010，p.211）

$h(t)={\text{p.v. }}{\frac {1}{\pi t}}$

因此可如此表示

$H(u)=h*u$

然而，事前此特性可能只有對緊支撐之分布 u定義。由於緊支撐函數在 L^p 上是稠密的，因此此項特性可能嚴格成立。另一角度來看，也可使用 h(t) 其微分之特性來證明

$H(u)(t)={\frac {d}{dt}}\left({\frac {1}{\pi }}(u*\log |\cdot |)(t)\right)$

在大部分的用途，希爾伯特轉換可被視為是一旋積。舉例而言，旋積與希爾伯特轉換具備下列可交換的特性

$H(u*v)=H(u)*v=u*H(v)$

若 u 和 v 為緊支撐分布，則此項論述嚴格成立，在這個狀況下

$h*(u*v)=(h*u)*v=u*(h*v)$

不變性

希爾伯特轉換在空間 L²(R) 上有下列特性

• 可與算子 T_aƒ(x) = ƒ(x + a) 交換，對所有實數 a
• 可與算子 M_λƒ(x) = ƒ(λx) 交換，對所有 λ > 0
• 可與鏡射 Rƒ(x) = ƒ(−x) 反交換

實際上，有更大一部分的算子可與希爾伯特轉換交換。群組 SL(2,R) 由幺正算符 U_g 可在空間 L²(R) 上由以下式子表示

$\displaystyle {U_{g}^{-1}f(x)=(cx+d)^{-1}f\left({ax+b \over cx+d}\right),\,\,\,g={\begin{pmatrix}a&b\\c&d\end{pmatrix}}}$

希爾伯特轉換例子

注意：有些作者，例如Bracewell，將我們的$-{\mathcal {H}}$當作其正轉換的定義。這樣的結果就是下表右行要乘上一個負號。

離散希爾伯特轉換

圖 1: 頻寬被限制在95%奈奎斯特頻率之濾波器頻率響應

圖 2: 高通頻率響應之希爾伯特轉換濾波器

圖 3.

圖 4. cos(wt)函數之希爾伯特轉換為 sin(wt)。此圖顯示了sin(wt)函數與一個利用MATLAB函式庫 hilbert(­­­­·)計算之近似希爾伯特轉換的差異

對於一離散函數 u[n]，以及其 離散傅利葉轉換 函數 U(ω)，可推得其希爾伯特轉換為:

$H(u)[n]=\scriptstyle {DTFT}^{-1}\displaystyle \{U(\omega )\cdot \sigma _{H}(\omega )\}$

其中

$\sigma _{H}(\omega )\ {\stackrel {\mathrm {def} }{=}}\ {\begin{cases}e^{+i\pi /2},&-\pi <\omega <0\\e^{-i\pi /2},&0<\omega <\pi \\0,&\omega =-\pi ,0,\pi \end{cases}}$

此外，根據摺積定律，另一個相等的方程式為:

$H(u)[n]=u[n]*h[n]$

其中

$h[n]\ {\stackrel {\mathrm {def} }{=}}\ \scriptstyle {DTFT}^{-1}{\big \{}\displaystyle \sigma _{H}(\omega ){\big \}}={\begin{cases}0,&{\mbox{for }}n{\mbox{ even}}\\{\frac {2}{\pi n}}&{\mbox{for }}n{\mbox{ odd}}\end{cases}}$

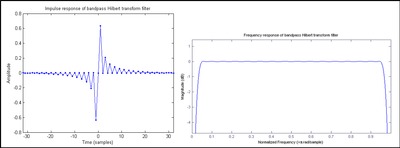
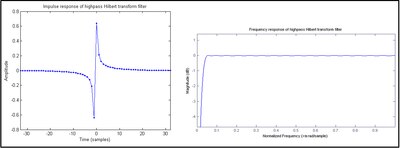
當摺積經由數值運算後，一FIR 近似將取代h[n]，如 圖 1所示，可以見到頻率響應在通帶之兩端(0與奈奎斯特頻率)的陡降，形成一帶通濾波器。其中高頻部分可藉由一FIR濾波器回復，如 圖 2所示。然而實際上，一個經過適當取樣的 u[n] 序列在高頻部分已經不具有可用的分量。當脈衝響應持續越久，低頻部分也可以被回復。

用FIR近似h[n]的時候，交疊儲存法是一個對於很長的u[n] 序列做摺積運算的有效方法。有時候陣列FFT{h[n]}會被σ_H(ω)相對應之取樣序列所取代。如此將會有與週期疊加函數做摺積之效果:

$h_{N}[n]\ {\stackrel {\text{def}}{=}}\ \sum _{m=-\infty }^{\infty }h[n-mN]$

圖 3比較了h_N[n]之半周期與一相同長度分量之h[n]。兩者之間之差異與兩者之長度皆不短於區段長度(N)之現象為失真的來源，且失真可經由增加區段長度與交疊參數來有效減少。

MATLAB中有一函數 hilbert(u,N)，此函數會回傳一複數序列，其中虛部序列為 u[n]之離散希爾伯特轉換近似，實部序列為原本輸入之序列，所以這樣的複數輸出等於是 u[n]的分析訊號。與前述類似， hilbert(u, N) 只使用來自 sgn(ω)分佈的取樣，因此是與 h_N[n] 的摺積。如前段所述，失真可藉由選擇比實際之u[n]序列更大的N與捨棄適當數量的輸出取樣來有效減少。圖 4為這種失真的一個例子。

相關條目

• 卷積
• 希爾伯特-黃轉換

參考文獻

• Bracewell, R. The Fourier Transform and Its Applications 2nd ed. McGraw-Hill. 1986.  引文格式1维护：冗余文本 (link)
• Carlson, Crilly, and Rutledge. Communication Systems 4th ed. 2002.  引文格式1维护：冗余文本 (link)
• Grafakos, Loukas, Classical and Modern Fourier Analysis, Pearson Education, Inc.: 253–257, 2004, ISBN 0-13-035399-X .
• Pichorides, S., On the best value of the constants in the theorems of Riesz, Zygmund, and Kolmogorov, Studia Mathematica, 1972, 44: 165–179 
• Riesz, Marcel, Sur les fonctions conjuguées, Mathematische Zeitschrift, 1928, 27 (1): 218–244, doi:10.1007/BF01171098 
• Duoandikoetxea, J., Fourier Analysis, American Mathematical Society, 2000, ISBN 0-8218-2172-5 
• Titchmarsh, E, Reciprocal formulae involving series and integrals, Mathematische Zeitschrift, 1926, 25 (1): 321–347, doi:10.1007/BF01283842 .
• Titchmarsh, E, Introduction to the theory of Fourier integrals 2nd, Oxford University: Clarendon Press, 19481986, ISBN 978-0-8284-0324-5 .
• Pandey, J.N., The Hilbert transform of Schwartz distributions and applications, Wiley-Interscience, 1996, ISBN 0-471-03373-1 
• Duistermaat, J.J., Distributions, Birkhäuser, 2010, ISBN 978-0-8176-4672-1, doi:10.1007/978-0-8176-4675-2 

外部連結

• another exposition — Hilbert transform properties
• Mathworld Hilbert transform — Contains a table of transforms
• Analytic Signals and Hilbert Transform Filters
• Hilbert Transform — Contains small table of transforms
• Easy Fourier Analysis hints to compute Hilbert transform in Time domain.