在数学中,离散时间傅里叶变换(DTFT,Discrete-time Fourier Transform)是傅里叶分析的一种形式,适用于连续函数的均匀间隔采样。离散时间是指对采样间隔通常以时间为单位的离散数据(样本)的变换。仅根据这些样本,它就可以产生原始连续函数的连续傅里叶变换的周期求和的以频率为变量的函数。在采样定理所描述的一定理论条件下,可以由DTFT完全恢复出原来的连续函数,因此也能从原来的离散样本恢复。DTFT本身是频率的连续函数,但可以通过离散傅里叶变换(DFT)很容易计算得到它的离散样本(参见对DTFT采样),而DFT是迄今为止现代傅里叶分析最常用的方法。
这两种变换都是可逆的。离散时间傅里叶逆变换得到的是原始采样数据序列。离散傅里叶逆变换是原始序列的周期求和。快速傅里叶变换(FFT)是用于计算DFT的一个周期的算法,而它的逆变换会产生一个周期的离散傅里叶逆变换。
一组离散的实数或复数:x[n](n 为所有整数)的离散时间傅里叶变换是产生以频率为变量的周期函数的一个傅里叶级数。当频率变量 ω 的单位是归一化的弧度/样本时,周期为 2π,而傅里叶级数为:
![{\displaystyle X_{2\pi }(\omega )=\sum _{n=-\infty }^{\infty }x[n]\,e^{-i\omega n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b912dd8998ca4ec2d477f047c6aef79c6a55f317) | | |
此频率域函数的性质源于泊松求和公式。令 X(f) 为任意函数 x(t) 的傅里叶变换,采样间隔为 T(秒),等价于序列 x[n](或与之成正比),即 ![{\displaystyle T\cdot x(nT)=x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca2ca9463d6b6da9fa9f28f0838eb87419b42d2) 。则以傅里叶级数表示的周期函数是 X(f) 的周期求和。要用以赫兹(周期/秒)为单位的频率
。则以傅里叶级数表示的周期函数是 X(f) 的周期求和。要用以赫兹(周期/秒)为单位的频率  的话就会是:
的话就会是:
![{\displaystyle X_{1/T}(f)=X_{2\pi }(2\pi fT)\ {\stackrel {\mathrm {def} }{=}}\sum _{n=-\infty }^{\infty }\underbrace {T\cdot x(nT)} _{x[n]}\ e^{-i2\pi fTn}\;{\stackrel {\mathrm {Poisson\;f.} }{=}}\;\sum _{k=-\infty }^{\infty }X\left(f-k/T\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff9b932cdb07bb87e03786d0705c557766d63f23) | | |
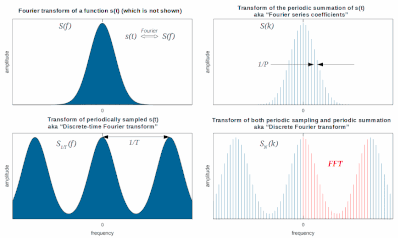 图一. 傅立叶变换(左上)和左下的其周期求和(DTFT)的图示。右下角显示了用离散傅里叶变换(DFT)计算DTFT的采样。
图一. 傅立叶变换(左上)和左下的其周期求和(DTFT)的图示。右下角显示了用离散傅里叶变换(DFT)计算DTFT的采样。
整数 k 的单位为转/样本,采样频率是 1/T,fs(样本/秒)。因而 X1/T(f) 含有移位 fs 倍数赫兹了的 X(f) 的精确副本,并加和在一起。对于足够大的 fs ,可以在区间 [−fs/2, fs/2] 有很少或没有失真(混疊)地观察到 k=0 项。在图1中,该左上角分布的末端在左下图中被周期求和的混叠遮盖住了。
我们还注意到  是
是  的傅里叶变换。因此,DTFT的另一个定义为:[note 1]
的傅里叶变换。因此,DTFT的另一个定义为:[note 1]
![{\displaystyle X_{1/T}(f)={\mathcal {F}}\left\{\sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eff3beb99f3510f9a94ba158b21018f980a6c6a6) | | |
调制的狄拉克梳状函数(或冲击串、冲击序列)是一个数学抽象,有时被称为脉冲采样。[1]
频谱的周期性与混叠[编辑]
频谱周期性[编辑]
 具有周期性:
具有周期性:
显然有:
频谱混叠[编辑]
根据DTFT的定义,有

即,f(nT)的DTFT是f(t)的傅里叶变换以Ω为周期的延拓,这也从另一个角度证明了DTFT的周期性。很显然,如果f(t)的频谱带不限于Nyquist间隔([-Ω/2, Ω/2]),f(nT)的DTFT必然发生混叠(aliasing),如右图所示。混叠使得信号的低频部分被高频部分“污染”,造成信号的失真。为避免这种情况,通常在进行进一步的数字信号处理之前要对采样序列进行抗混叠滤波(anti-aliasing filtering),这一处理通常是由低通滤波器除去高频分量实现的。
DTFT与DFT[编辑]
DFT(离散傅里叶变换)是对离散周期信号的一种傅里叶变换,对于有限长信号,则相当于对其周期延拓进行变换。在频域上,DFT的离散谱是对DTFT连续谱的等间隔采样。

DTFT与DFT频率解析度[编辑]
 图2 DTFT与DFT。上图为10点DFT,下图为补零到12点的DFT。
图2 DTFT与DFT。上图为10点DFT,下图为补零到12点的DFT。
N 点序列f(n)(n=0, ... ,N-1)的DFT离散谱对应于对f(nT) 连续谱(即DTFT)的N点采样,因此DFT的频率解析度 。为了提高频率解析度,可以考虑增加在DTFT频域上的采样点数,对偶在时域就是增加对时域信号 f(n) 的采样数。对于有限长信号f(n),在时刻0 至N-1以外的值实际上是已知的——都为0。因此,只要在序列f(n) 前后补零就增加了在时域的采样,假设在f(n)前后补上M-N(其中M>N)个零,则补零之后序列的DFT的频率解析度就相应提高到
。为了提高频率解析度,可以考虑增加在DTFT频域上的采样点数,对偶在时域就是增加对时域信号 f(n) 的采样数。对于有限长信号f(n),在时刻0 至N-1以外的值实际上是已知的——都为0。因此,只要在序列f(n) 前后补零就增加了在时域的采样,假设在f(n)前后补上M-N(其中M>N)个零,则补零之后序列的DFT的频率解析度就相应提高到 。相关证明如下:
。相关证明如下:
- 假设在f(n)之后补上M-N个0,则其DFT为

- 由于n=N,...,M-1时f(n)=0,所以有

通过上式可以清楚的看到,f(n)补零之后的DFT增加了在f(nT)连续频域谱上的采样。采样点数从N增加到M,从而提高了DFT频谱的解析度。另一方面,补零之后在频域采样的位置发生了变化,因此可以观察到其他的频点。
如图2所示,对信号 (其中
(其中 ,
, )按照
)按照 采样。
采样。 与
与 对应的数字角频率分别为
对应的数字角频率分别为 ,
, 。上图为取10个采样点作DFT,可在0.6π处看到对应的频率分量,然而由于采样点少,看不到0.5π处的分量。下图为补2个零之后的DFT离散谱,可以见到离散谱的分辨率提高到了π/6,而且能够观察到10点DFT无法看到的0.5π频率分量。另外,虚线为DTFT连续谱,可见,DFT确实是在频域对DTFT的采样。
。上图为取10个采样点作DFT,可在0.6π处看到对应的频率分量,然而由于采样点少,看不到0.5π处的分量。下图为补2个零之后的DFT离散谱,可以见到离散谱的分辨率提高到了π/6,而且能够观察到10点DFT无法看到的0.5π频率分量。另外,虚线为DTFT连续谱,可见,DFT确实是在频域对DTFT的采样。
但是我们可以看到,即使是10点DTFT的连续谱也不能分辨 与
与 (只有一个峰)。这是因为10点DTFT的分辨率为fs/10 = 100 Hz,大于f1 - f2 = 50 Hz。所以,只有采样的点数超过20(即分辨率小于50Hz),才能分辨出
(只有一个峰)。这是因为10点DTFT的分辨率为fs/10 = 100 Hz,大于f1 - f2 = 50 Hz。所以,只有采样的点数超过20(即分辨率小于50Hz),才能分辨出 与
与 这两个频率分量(如图3所示)。而前面提到的对有限长信号补零作DFT以提高频谱分辨率的说法,也只是针对在DTFT连续谱上采样而言,只有增加采样点数和提高采样频率才能真正提高离散谱的分辨率。
这两个频率分量(如图3所示)。而前面提到的对有限长信号补零作DFT以提高频谱分辨率的说法,也只是针对在DTFT连续谱上采样而言,只有增加采样点数和提高采样频率才能真正提高离散谱的分辨率。
以DFT近似DTFT[编辑]
前面提到,在时间序列前后补零之后作DFT可以增加在DTFT上的采样点数。可以想见,如果补上无穷多个零,则可以得到无穷多个DTFT连续谱上的采样点,从而以DFT逼近DTFT。即,使得离散谱的分辨率足够小,即为连续谱。
这种想法显然是错误的,首先应该注意到,DFT的周期型,虽然进行DFT的序列x(k)是有限长序列,但是DFT隐含对x(k)的周期延拓,x(k)是信号序列,周期延拓后还是原来的信号,如果对x(k)进行补零后,1.补零后序列长度不是原信号序列长度的整数倍,那么补零后的序列就不再是原信号的序列,已经破坏了原信号的信息。2.补零后序列长度是原信号序列的整数倍,原信号信息没有被破坏,仍能通过DFT后获得原信号信息,但是补零后序列的DFT虽然频率步长小了,可以观察的频谱信息更丰富了,但是这些额外的频谱并不是原信号的频谱,而是窗函数的频谱信息,也就是包络线是窗函数的形状。所以补零并没有给出关于原信号频谱的更多信息。补零并不能使补零后的DFT结果的包络线和原信号频谱的包络线一致。
DTFT与Z变换[编辑]
离散时间傅里叶变换可以被看作Z变换的特例。Z变换被定义为:

如果在z平面的单位圆( )上对信号
)上对信号 做Z变换:
做Z变换:

此即为 的离散时间傅里叶变换。因此通常用
的离散时间傅里叶变换。因此通常用 ,而不是
,而不是 表示DTFT。
表示DTFT。
- ^ 事实上Eq.2通常解释如下:

参考文献[编辑]
- Alan V. Oppenheim and Ronald W. Schafer : Discrete-Time Signal Processing, Prentice Hall Signal Processing Series, ISBN 978-0-13-754920-7
- Boaz Porat : A Course in Digital Signal Processing, pp. 27-29, pp. 104-105, John Wiley and Sons, ISBN 978-0-471-14961-3
- Sophocles J. Orfanidis : Introduction to Signal Processing, Prentice Hall International, Inc., ISBN 7-32-03059-6
- ^ Rao, R. Signals and Systems. Prentice-Hall Of India Pvt. Limited. [2015-11-27]. ISBN 9788120338593. (原始内容存档于2020-09-07).



![{\displaystyle X_{2\pi }(\omega )=\sum _{n=-\infty }^{\infty }x[n]\,e^{-i\omega n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b912dd8998ca4ec2d477f047c6aef79c6a55f317)
![{\displaystyle T\cdot x(nT)=x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca2ca9463d6b6da9fa9f28f0838eb87419b42d2)

![{\displaystyle X_{1/T}(f)=X_{2\pi }(2\pi fT)\ {\stackrel {\mathrm {def} }{=}}\sum _{n=-\infty }^{\infty }\underbrace {T\cdot x(nT)} _{x[n]}\ e^{-i2\pi fTn}\;{\stackrel {\mathrm {Poisson\;f.} }{=}}\;\sum _{k=-\infty }^{\infty }X\left(f-k/T\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff9b932cdb07bb87e03786d0705c557766d63f23)


![{\displaystyle X_{1/T}(f)={\mathcal {F}}\left\{\sum _{n=-\infty }^{\infty }x[n]\cdot \delta (t-nT)\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eff3beb99f3510f9a94ba158b21018f980a6c6a6)






















