逻辑斯谛函数

邏輯斯諦函數(英語:logistic function)是一种常见的S型函数,其函數圖像稱為逻辑斯谛曲线(英語:logistic curve)。简单的逻辑斯谛函数可用下式表示:
其中:
- x0为S形曲线中点的x值;
- L为曲线的最大值
- k为逻辑斯谛增长率或曲线的陡度。[1]
当x趋向于正无穷时,f(x)的值逼近L,而x趋向于负无穷时,f(x)的值逼近0。
逻辑斯谛函数应用领域广泛,包括生物学(特别是生态学)、數理生物學、化學、人口学、经济学、地球科学、数学心理学、概率、社会学、政治学、语言学、统计学和人工神经网络等。例如,广义逻辑斯谛曲线可以模仿一些情况人口增长(P)的S形曲线。起初阶段大致是指数增长;然后随着开始变得饱和,增长变慢;最后,达到成熟时增长停止。
歷史[编辑]

逻辑斯谛函数是皮埃尔·弗朗索瓦·韦吕勒于1838年至1847年间发表的三篇论文中提出的,他在阿道夫·凯特勒的指导下,通过调整指数增长模型,将其设计为人口增长模型。[2]韦吕勒在1830年代中期设计了该函数,并在1838年发表了一个简短的说明,[1]然后在1844年进一步分析并命名了这个函数(发表于1845年)[3]第三篇论文调整了比利时人口增长模型中的修正项。[4]
增长的初始阶段近似于指數增長(几何级数);然后,随着增长逐渐饱和,曲线放缓至接近线性,在成熟阶段,增长停止。原本选用“逻辑斯谛”(法語:logistique,英語:logistic)一词时,韦吕勒没有解释其原由,但这可能是为了区别于对数曲线,[5][a]并与算术和几何进行对比。在提出该增长模型前,他讨论了算术增长和几何增长(他称之为“对数曲线”,其现代通称是指数曲线),因此“逻辑斯谛增长”可能是通过类比命名的,“逻辑斯谛”来自古希腊语λογῐστῐκός(logistikós),是指古希腊数学的一个分支。[b]“逻辑斯谛函数”中的“逻辑”与逻辑学(logic)和军队后勤/物流(logistics,自法语logis)均没有关系。
数学特性[编辑]
标准逻辑斯谛函数的参数设定为, , ,即
实际上,由于指数函数的特性,函数的取值很快会逼近极限,x在很小的实数范围内(例如[−6, +6])的取值就足以计算标准逻辑斯谛函数的极限。
标准逻辑斯谛函数具有如下对称性:
因此,是奇函数。
标准逻辑斯谛函数可视为双曲正切函数的偏移和缩放:
或
推导过程如下:
导数[编辑]
逻辑斯谛分布的均值为x0,方差为π2/3k2。
积分[编辑]
标准逻辑斯谛函数的不定积分可用换元积分法求得,令,,去掉積分常數,得到其不定积分:
在人工神经网络中,它称作线性整流函数,(缩放后)可视为平滑近似的斜坡函数,类似于逻辑斯谛函数(缩放后)是平滑近似的单位阶跃函数。
逻辑斯谛微分方程[编辑]
标准逻辑斯谛函数是简单的一阶非线性常微分方程的解:
边界条件为。该方程是逻辑斯谛映射的连续版本。注意倒数逻辑斯谛函数是简单的一阶线性常微分方程的解。[6]
邏輯斯諦差分方程[编辑]
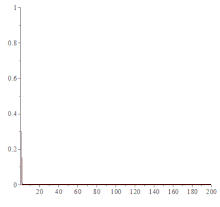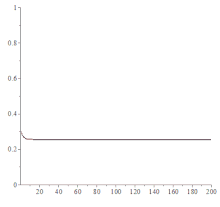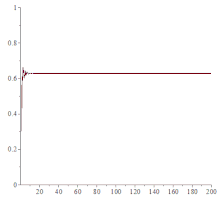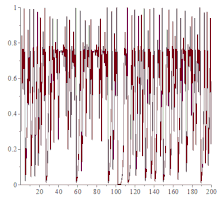
是混沌理论的一个模型。[7][8]这个函数对初始值和参数的变化很敏感,往往微小的变化会引起混沌。如图所示,当x1=0.3,参数k从0.1变到4时,系统变化很大。
- 当k由0.1变到1时,曲线很快趋向于0
- 当k继续增加,曲线由0.3上升到 一个稳定值
- k继续增加,曲线出现摆动,有2个稳定值。
- k继续增加, 曲线相继出现4个、8个、16个、32个....稳定值
- k增加到一个临界值,系统进入混沌状态。
- k再增加,系统突然垮塌。
变化[编辑]

应用[编辑]
生态学:种群增长模型[编辑]

逻辑斯谛方程的一个典型应用是种群(或人口)增长的通用模型(另见种群动态),最初由皮埃尔·弗朗索瓦·韦吕勒在1838年提出,其中繁殖率与现状种群数量和可用资源量成正比,其他一切都条件均等。韦吕勒方程是他在阅读马尔萨斯的论文《An Essay on the Principle of Population 》后发表的,该论文描述了简单(无约束条件)指數增長的馬爾薩斯模型。韦吕勒推导出他的逻辑斯谛方程来描述生物种群的自限性增长。该方程于1911年被A. G. McKendrick用于描述肉汤中细菌的生长,他使用非线性参数估计的方法进行了实验测试。[9]在约翰斯·霍普金斯大学的Raymond Pearl(1879–1940)和Lowell Reed(1888–1966)于1920年使用该方程后,这一方程有时也称为Verhulst-Pearl方程。[10]另一位科学家阿弗雷德·洛特卡在1925年再次推导出该方程,称其为种群增长律(law of population growth)。
令P为种群(人口)规模(生态学经常用N代替),t代表时间,该模型用以下微分方程表示:
方程中,早期的几乎无阻力的增长率来自+rP。增长率r代表种群(人口)数量P在一个单位时间内的增长比例。后来,随着人口的增长,第二项-rP2/K变得几乎和第一项一样大,种群P内的个体之间开始争夺某些关键资源(例如食物或生存空间)而相互干扰。这种对抗效应称为“瓶颈”,由参数K代表。竞争会降低总合增长率,直到P停止增长(种群/人口成熟)。方程的解(P0为初始种群/人口数量)为
其中:
可以说,K是P的极限值,即经过无限长时间后(或在有限时间内近似),种群(人口)规模所能达到的最大值。须注意,只要初始值,无论取值多少,种群数量都会渐近环境承载力的值,包括的情况下。
生态学中有时称一个物种是r策略或K策略的,这是指它们在自然选择过程形成的生物生命週期策略。选取变量的量纲,使n代表以环境承载力单位计的种群数量,代表以的单位计量的时间,得出无量纲微分方程:
时变承载力[编辑]
由于环境条件会影响环境承载力,因此它可能是随时间变化的,,得出以下数学模型:
其中一种特别重要的情况是承载力随时期以T为周期变化的情况:
可见,只要初始值,无论具体取值为多少,会逼近一个周期为的周期解。
的典型取值为1年,在此情况下,可表示天气条件的周期性变化。
另一个有趣的一般化情形是考虑承载能力K(t)作为关于较早时间的种群数量的函数,以表示种群改变其所处环境的延迟。这就构成了一个逻辑斯谛时滞方程,[11]它具有非常丰富的行为,在某些参数范围内呈现双稳定,以及单调衰减至零、平滑指数增长、间断无限增长(即多个S形)、间断增长或交替到平稳水平、振荡接近稳定水平、持续振荡、有限时间奇异点以及有限时间死亡。
统计学和机器学习[编辑]
逻辑斯谛函数在统计学中有多种应用。例如,它们是逻辑斯谛分布的累积分布函数,它们可用于模拟國際象棋棋手在埃洛等级分系统下击败对手的概率。以下是一些更具体的案例。
邏輯迴歸[编辑]
邏輯斯諦迴歸使用逻辑斯谛函数来模拟一个事件的概率p如何可能会受到一个或多个解释变量的影响:一个案例模型如下
其中x为解释变量,a和b为欲拟合的模型参数,f为标准逻辑斯谛函数。
邏輯斯諦迴歸和其他对数线性模型也常用于机器学习。将逻辑斯谛函数推广至多元输入情景即为Softmax激活函数,用于多元罗吉斯回归。
神经网络[编辑]
医学:肿瘤生长模型[编辑]
在医学上,逻辑斯谛微分方程可用于肿瘤生长的建模。这一用法可视为上述的生态学/人口学模型的延伸。以表示肿瘤在时间的大小,其变化动态遵循
属于以下类型:
其中为肿瘤增殖率。
如果采用化疗产生对数杀伤效果,则等式修改为
其中为治疗引起的肿瘤死亡率。在理想化的极长的治疗下,可模型化为周期为的周期函数或(在持续的输液治疗下)常数函数,有
即,如果平均治疗引起的肿瘤死亡率大于基线增殖率,则疾病能被根除。当然,这是一个过于简化的生长和治疗模型(例如没有考虑克隆抗性现象)。
医学:传染病模型[编辑]
在人群中未被免疫的新型传染性病原体,通常会在早期呈指数级传播,有大量易感个体尚未被感染。例如2020年初,导致2019冠状病毒病的SARS-CoV-2病毒在多国的感染过程中呈现出指数级增长。[12]此后,易感宿主减少(持续感染直到超过群体免疫阈值)或通过社交距离措施减少潜在宿主的被传染概率等因素,可能使呈指数增长的传染曲线首先线性化,然后趋缓,达到最大值。[13]
逻辑斯谛函数或相关的函数(例如龚珀兹函数)通常以描述性或现象学方的式使用,因为它们非常符合早期的指数上升,也符合随着人群形成群体免疫而最终趋于平稳的趋势。它与流行病的实际模型不同,后者试图根据大流行的动态(例如接触率、潜伏期、社交距离等)来描述感染状态。不过,一些简单的模型有逻辑斯谛解。[14][15][16]
早期COVID-19病例数建模[编辑]

广义逻辑斯谛函数(又称Richards增长曲线)已应用于对COVID-19爆发的早期阶段建模。[17]研究者将广义逻辑斯谛函数拟合到累计感染病例数(称为传染轨迹)。文献中对广义逻辑斯谛函数有不同的参数化。一种常用的形式是:
其中取实数,为正实数。曲线的灵活性由赋予:(i)若,则曲线衰减为逻辑斯谛函数,(ii)若收敛至0,则曲线收敛至龚珀兹函数。在传染病模型中,, 和分别代表传染病最终的规模、感染率和滞后期。见右侧的范例的传染轨迹,其中设定为。

在流行病学建模中,使用类似广义逻辑斯谛函数的增长函数的好处之一是它相对容易应用于多级模型框架,其中来自不同地理区域的信息可以汇总在一起。
化学:反应模型[编辑]
自催化反应中,反应物和产物的浓度遵循逻辑斯谛函数。例如燃料电池阴极中不含铂族金属(PGM-free)的氧还原反应催化剂的劣化遵循逻辑斯谛衰减函数,[18]表明这是一种自催化分解机制。
物理:费米-狄拉克分布[编辑]
费米子在热平衡系统的能量状态上的统计分布遵循逻辑斯谛函数。特别地,根据费米-狄拉克统计,它是每个可能的能级被一个费米子占据的概率分布。
语言学:语言变化[编辑]
语言学中,逻辑斯谛函数可用于对語言變化进行建模:[19]一种最初处于边缘地位的新词随着时间的推移开始传播得更快,然后传播速度随着其普及而减慢。
经济学和社会学:创新扩散[编辑]
逻辑斯谛函数可用于描绘一项发明创新在其生命周期内扩散的过程.
参见[编辑]
注释[编辑]
参考文献[编辑]
- ^ 1.0 1.1 Verhulst, Pierre-François. Notice sur la loi que la population poursuit dans son accroissement (PDF). Correspondance Mathématique et Physique. 1838, 10: 113–121 [3 December 2014].
- ^ Cramer, J. S. The origins of logistic regression (PDF) (技术报告) 119. Tinbergen Institute: 167–178. 2002 [2022-05-05]. doi:10.2139/ssrn.360300. (原始内容存档 (PDF)于2022-07-21).
|issue=被忽略 (帮助) - ^ Verhulst, Pierre-François. Recherches mathématiques sur la loi d'accroissement de la population [Mathematical Researches into the Law of Population Growth Increase]. Nouveaux Mémoires de l'Académie Royale des Sciences et Belles-Lettres de Bruxelles. 1845, 18: 8 [18 February 2013].
Nous donnerons le nom de logistique à la courbe [We will give the name logistic to the curve]
- ^ Verhulst, Pierre-François. Deuxième mémoire sur la loi d'accroissement de la population. Mémoires de l'Académie Royale des Sciences, des Lettres et des Beaux-Arts de Belgique. 1847, 20: 1–32 [18 February 2013]. (原始内容存档于2016-05-18).
- ^ Shulman, Bonnie. Math-alive! using original sources to teach mathematics in social context. PRIMUS. 1998, 8 (March): 1–14. doi:10.1080/10511979808965879.
The diagram clinched it for me: there two curves labeled "Logistique" and "Logarithmique" are drawn on the same axes, and one can see that there is a region where they match almost exactly, and then diverge.
I concluded that Verhulst's intention in naming the curve was indeed to suggest this comparison, and that "logistic" was meant to convey the curve's "log-like" quality. - ^ Kocian, Alexander; Carmassi, Giulia; Cela, Fatjon; Incrocci, Luca; Milazzo, Paolo; Chessa, Stefano. Bayesian Sigmoid-Type Time Series Forecasting with Missing Data for Greenhouse Crops. Sensors. 7 June 2020, 20 (11): 3246. Bibcode:2020Senso..20.3246K. PMC 7309099
 . PMID 32517314. doi:10.3390/s20113246
. PMID 32517314. doi:10.3390/s20113246  .
.
- ^ Garnett P. Williams Chaos Theory Tamed chapter 10
- ^ Edgar Peters Chaos and Order in the Capital Market p7
- ^ A. G. McKendricka; M. Kesava Paia1. XLV.—The Rate of Multiplication of Micro-organisms: A Mathematical Study. Proceedings of the Royal Society of Edinburgh. January 1912, 31: 649–653 [2022-05-05]. doi:10.1017/S0370164600025426. (原始内容存档于2021-11-20).
- ^ Raymond Pearl & Lowell Reed. On the Rate of Growth of the Population of the United States (PDF) 6 (6). June 1920: 275 [2022-05-05]. (原始内容存档 (PDF)于2021-07-10).
|journal=被忽略 (帮助) - ^ Yukalov, V. I.; Yukalova, E. P.; Sornette, D. Punctuated evolution due to delayed carrying capacity. Physica D: Nonlinear Phenomena. 2009, 238 (17): 1752–1767. Bibcode:2009PhyD..238.1752Y. S2CID 14456352. arXiv:0901.4714
 . doi:10.1016/j.physd.2009.05.011.
. doi:10.1016/j.physd.2009.05.011.
- ^ Worldometer: COVID-19 CORONAVIRUS PANDEMIC. [2022-05-05]. (原始内容存档于2020-03-22).
- ^ Villalobos-Arias, Mario. Using generalized logistics regression to forecast population infected by Covid-19. 2020. arXiv:2004.02406
 [q-bio.PE].
[q-bio.PE].
- ^ Postnikov, Eugene B. Estimation of COVID-19 dynamics "on a back-of-envelope": Does the simplest SIR model provide quantitative parameters and predictions?. Chaos, Solitons & Fractals. June 2020, 135: 109841. Bibcode:2020CSF...13509841P. PMC 7252058
 . PMID 32501369. doi:10.1016/j.chaos.2020.109841.
. PMID 32501369. doi:10.1016/j.chaos.2020.109841.
- ^ Saito, Takesi. A Logistic Curve in the SIR Model and Its Application to Deaths by COVID-19 in Japan. medRxiv. June 2020 [July 20, 2020]. S2CID 220068969. doi:10.1101/2020.06.25.20139865. (原始内容存档于2022-04-30).
- ^ Reiser, Paul A. Modified SIR Model Yielding a Logistic Solution. 2020. arXiv:2006.01550
 [q-bio.PE].
[q-bio.PE].
- ^ Lee, Se Yoon; Lei, Bowen; Mallick, Bani. Estimation of COVID-19 spread curves integrating global data and borrowing information. PLOS ONE. 2020, 15 (7): e0236860. Bibcode:2020PLoSO..1536860L. PMC 7390340
 . PMID 32726361. arXiv:2005.00662
. PMID 32726361. arXiv:2005.00662  . doi:10.1371/journal.pone.0236860
. doi:10.1371/journal.pone.0236860  .
.
- ^ Yin, Xi; Zelenay, Piotr. Kinetic Models for the Degradation Mechanisms of PGM-Free ORR Catalysts. ECS Transactions. 13 July 2018, 85 (13): 1239–1250 [2022-05-05]. OSTI 1471365. S2CID 103125742. doi:10.1149/08513.1239ecst. (原始内容存档于2022-05-05).
- ^ Bod, Hay, Jennedy (eds.) 2003, pp. 147–156
- Jannedy, Stefanie; Bod, Rens; Hay, Jennifer. Probabilistic Linguistics. Cambridge, Massachusetts: MIT Press. 2003. ISBN 0-262-52338-8.
- Gershenfeld, Neil A. The Nature of Mathematical Modeling. Cambridge, UK: Cambridge University Press. 1999. ISBN 978-0-521-57095-4.
- Kingsland, Sharon E. Modeling nature: episodes in the history of population ecology. Chicago: University of Chicago Press. 1995. ISBN 0-226-43728-0.
- 埃里克·韦斯坦因. Logistic Equation. MathWorld.
外部链接[编辑]
- L.J. Linacre, Why logistic ogive and not autocatalytic curve? (页面存档备份,存于互联网档案馆), accessed 2009-09-12.
- https://web.archive.org/web/20060914155939/http://luna.cas.usf.edu/~mbrannic/files/regression/Logistic.html
- Modeling Market Adoption in Excel with a simplified s-curve (页面存档备份,存于互联网档案馆)
- 埃里克·韦斯坦因. Sigmoid Function. MathWorld.
- Online experiments with JSXGraph (页面存档备份,存于互联网档案馆)














































![{\displaystyle f(t;\theta _{1},\theta _{2},\theta _{3},\xi )={\frac {\theta _{1}}{[1+\xi \exp(-\theta _{2}\cdot (t-\theta _{3}))]^{1/\xi }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29479f9d2bb480d1bf104fc0d84fcbaf00cf99f6)








