逻辑斯谛映射
單峰映射(英語:Logistic map)是種二次多項式的映射(遞迴關係式),是一個由簡單非線性方程式產生混沌現象的經典範例。這種映射因生物學家Robert May在1976年發表的一篇論文而著名,[1]一定程度上是离散时间的種群/人口模型,類似於皮埃尔·弗朗索瓦·韦吕勒的逻辑斯谛函数。[2]。單峰映射實質上是邏輯斯諦函數的差分方程,其數學表達為:
其中
- 是介於0和1之間的數,表示當前種群数量/人口數量與环境承载力的比值。
- 是正整數,是根據繁殖和死亡率而得出的數。
單峰映射的方程旨在描述以下兩個現象:
參數r通常取[0, 4]區間內的值,因此xn在[0, 1]上保持有界。r = 4的情景是dyadic映射及參數μ=2的帳篷映射的非線性變換。當r > 4時,種群數量會出現負值(該問題在更早前的同樣表現出混沌動態的Ricker模型中不會出現)。也可在[−2, 0]的區間內取r值,該情形下xn有界,處於[−0.5, 1.5]之間。[3]
r的值對結果的影響[编辑]
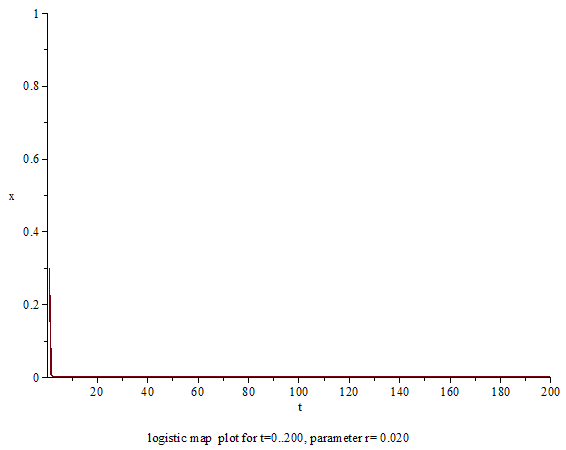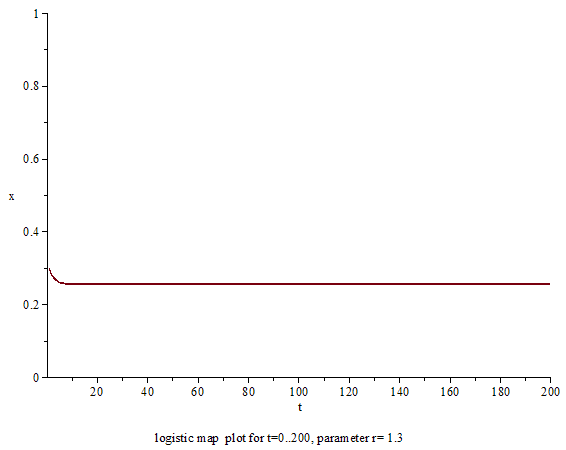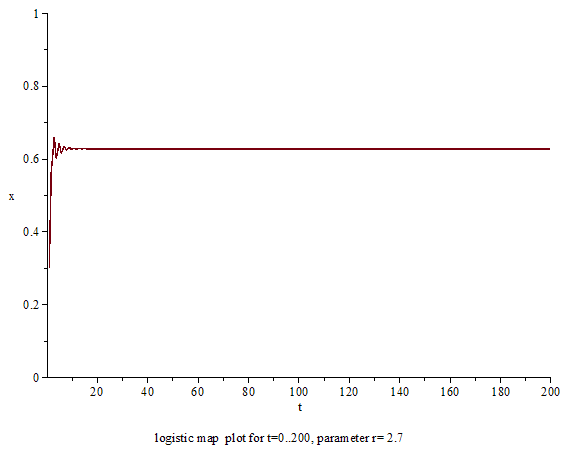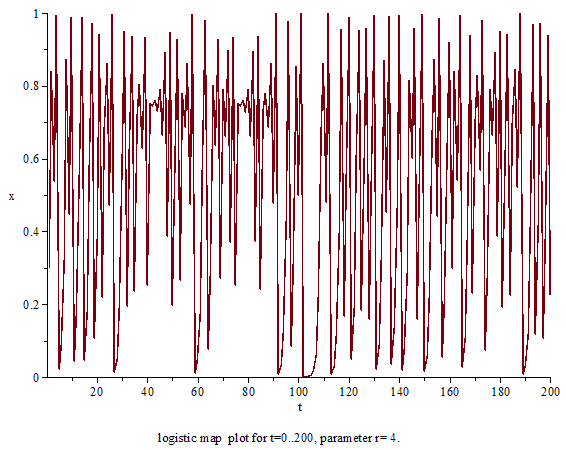
變化參數的值,其結果如下:
- 0和1之間:不論起始值數值為何,會越來越少,最後趨近於0。
- 1和2之間:不論起始值數值為何,會快速的趨近。
- 2和3之間:經過幾次迭代,也會越來越接近,但一開始會在這個值左右振動,而收斂速率是線性的。
- 3:仍然會越來越接近,但收斂速率极为缓慢,不是線性的。
- 3和(約3.45)之間:針對幾乎所有的初值,最後會在2個值之間持續的震盪,即最後會是a,b,a,b...的變化,其數值和有關。
- 3.45和大約3.54之間,針對幾乎所有的初值,最後會在4個值之間持續的震盪。
- 約大於3.54:最後會在8個、16個、32個值……之間持續的震盪,至於何時會令的值由n個到2n個,則和費根鮑姆常數有關。
- 約為3.5699:這樣的振動消失,整個系統開始在混沌的狀態之中。針對幾乎所有的初值,都不會出現固定週期的震盪,初值再微小的變化,隨著時間都會使結果產生明顯的差異,這就是典型混沌的特性。
- 大於3.5699:整個系統在混沌的狀態之中。不過,當中有些特定的值還是使系統變成非混沌,有週期性的結果,這些區間稱為「穩定岛」。例如當約大於3.82,會出現3個值的週期,再大一點出現6個值及12個值的週期。
- 當從大約3.5699到大約3.8284之間,系統混沌性質發展的現象有時會稱為Pomeau–Manneville場景,其特徵是週期性的震盪和非週期性的行為會穿插出現。此特徵可以應用在半導體元件中[4]。也有其他區域會使系統的週期為5個值,不管任意週期都存在某特定的,使週期為指定值。
- 大於4:針對幾乎所有的初值,系統最後都會超過区间[0,1]并且发散。
對於任一個值,最多只有一個穩定的極限環,若穩定極限環存在,幾乎所有的點最後都會趨近極限[5]:13。若某一個值有一個穩定的極限環,可能也有無限個不同週期的不穩定極限。
這些情況可用分枝圖表示,分枝圖中的橫軸是參數的數值,縱軸中顯示大部份初值下,穩態可能的值,若最後數值會在2個值中震盪,分枝圖上對應的數值就會有2點。若某特定值下,已無法明確的看到有幾個對應的點,當時系統可能已經在混沌狀態下。
分枝圖有自相似的特性。若將分枝圖中的部份展開,只取三個分支中的一個。其圖形會好像是原分枝圖縮放及扭曲後的結果。針對所有非混沌的參數都有此一特性。以此可以看出混沌和分形深入及明顯的關係。

單峰映射和混沌[编辑]

![x[n+1]-x[n] vs x[n] 动画](http://upload.wikimedia.org/wikipedia/commons/5/54/Logistic_map_phase_plot_of_x-n%2B1--x-n-_vs_x-n-.gif)
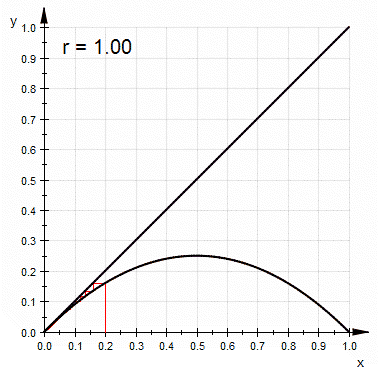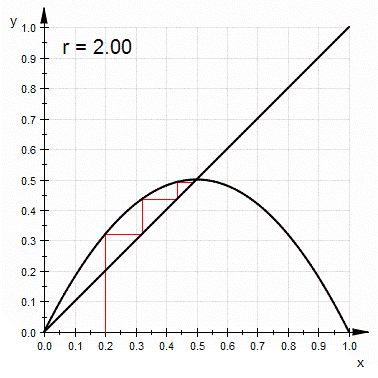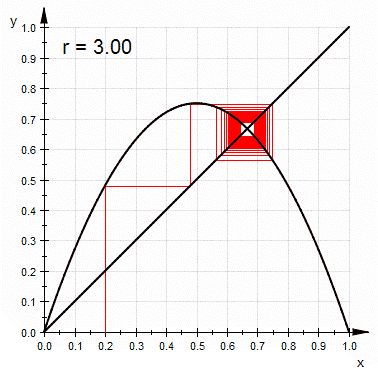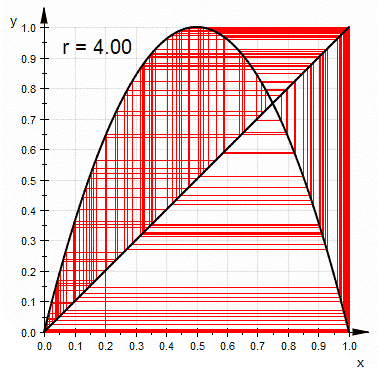
和其他混沌系統比較,單峰映射較為簡單,是一個說明混沌特性的很好的例子。簡單來說,混沌就是對初始條件的高度靈敏度。是在3.57及4之間的大部份數值都可以使單峰映射出現此一特性。對初始條件有高度靈敏度的常見原因是映射本身是對定義域的拉伸及摺疊。單峰映射的二次差分方程可視為是對於區間(0,1)拉伸及摺疊的過程。
利用二維及三維的相圖可以看出一些單峰映射的特性。以的單峰映射為例,二維相圖為一抛物線,但是若用繪製三維相圖,可看出進一步的結構,例如幾個一開始很接近的點在迭代後開始發散.特別是位在斜率較大位置的點。
拉伸及摺疊的結果使迭代的數列以指數形式發散(參照李亞普諾夫指數),可以用有混沌特性時,單峰映射的复杂及不可預測性說明這一點。事實上,數列的指數發散說明了混沌和不可預測性之間的關係:初值微小的誤差在迭代過程中會以指數成長的方式增加。因此當對於初始狀態的資訊中有微小的誤差時.對未來狀態的預測準確度也會隨迭代次數增加而快速變差。
由於映象是限制在實數數線的一段範圍內,其維度小於或等於1。依數值分析的結果,在r=3.5699456...時(剛開始混沌特性時),其關聯維度為0.500 ± 0.005[6](Peter Grassberger,1983)、豪斯多夫维数大約是0.538[7],而分形维数為0.5170976...[6]。

有些混沌系統可對於其未來狀態的可能性作準確的描述。若一個可能有混沌特性的動態系統存在吸引子,則存在一機率量測描述系統長期下,在吸引子各部份所花時間的比例。以的單峰映射而言,起始狀態在區間(0,1)中,而吸引子也在間(0,1)中,其機率量測對應參數的Β分布[8],其不變測度為。不可預期性和隨機不同,不過在一些情形下這二很類似,而且即使對單峰映射(或其他混沌系統)初值只有很少的資訊,仍然可以針對長期的分佈作某種程度的預測。
部份情形下的解[编辑]
在及的特殊情形下,單峰映射有解析解[9]。不過大部份情形下的通解只能以統計的方式預測[10]。 的解為[9][11]
其中初始條件參數是由求得。針對有理數的,有限次數的迭代後就會變成一個週期性的數列。不過幾乎所有的都是無理數,此時不會重複,因此沒有週期解。此解可以清楚的看出混沌的二個重要特徵:拉伸及摺疊。係數2n表示拉伸的指數成長,因此造成蝴蝶效应,也就是對初始值的高度靈敏性,而解中包括正弦函數的平方,使解摺疊在[0, 1]的範圍內。
的解為:
對於。此解沒有混沌的特性。由於對於不包括不穩定固定點0在內的,當n趨近無限大時會趨近於零,因此會趨近穩定的固定點。
r = 4時找任意週期的循環[编辑]
r = 4時,幾乎所有的初值都會使單峰映射出現混沌特性,不過也存在無限個初值會使單峰映射最後呈週期性變化,而且對於所有正整數,都存在一初值使單峰映射的週期為該正整數。可以利用單峰映射和位元位移映射之間的關係來找出任何週期的循環。若x依照單峰映射而y依照位元位移映射
則二個變數的關係如下:
- .
位元位移映射其名稱是因為當y以二進制表示時,映射會將二進制的數字左移一位。例如若數字是二進制的循環小數,循環節為001,則位元位移映射的序列為001001001... →010010010... →100100100... →001001001...,為週期為3的循環,循環節為010, 011, 100, 101, 110 時也會有類似情形,這些循環小數都可以轉換為對應的分數,上例若以分數表示為:1/7 → 2/7 → 4/7 → 1/7。轉換到r=4的單峰映射後,為611260467... → .950484434... → .188255099... → .611260467...。其他週期為3的循環也可以轉換為單峰映射。依相同方式也可以找出在 位元位移映射下,任意週期的循環,再轉換為單峰映射。
不過幾乎所有在區間[0, 1)的數字都是無理數,而初始值為無理數的位元位移映射沒有循環的特性,因此對應的單峰映射也沒有循環的特性。
相關條目[编辑]
參考資料[编辑]
- ^ May, Robert M. Simple mathematical models with very complicated dynamics. Nature. 1976, 261 (5560): 459–467. Bibcode:1976Natur.261..459M. PMID 934280. S2CID 2243371. doi:10.1038/261459a0. hdl:10338.dmlcz/104555
 .
.
- ^ "埃里克·韦斯坦因. Logistic Equation. MathWorld.
- ^ Tsuchiya, Takashi; Yamagishi, Daisuke. The Complete Bifurcation Diagram for the Logistic Map. Z. Naturforsch. February 11, 1997, 52a: 513–516.
- ^ Carson Jeffries; Jose Perez. Observation of a Pomeau–Manneville intermittent route to chaos in a nonlinear oscillator. Physical Review A. 1982, 26 (4): 2117–2122. Bibcode:1982PhRvA..26.2117J. doi:10.1103/PhysRevA.26.2117.
- ^ Collet, Pierre, and Jean-Pierre Eckmann, Iterated Maps on the Interval as Dynamical Systems, Birkhauser, 1980.
- ^ 6.0 6.1 Peter Grassberger and I. Procaccia. Measuring the strangeness of strange attractors. Physica D. 1983, 9 (1–2): 189–208. Bibcode:1983PhyD....9..189G. doi:10.1016/0167-2789(83)90298-1.
- ^ Peter Grassberger. On the Hausdorff dimension of fractal attractors. Journal of Statistical Physics. 1981, 26 (1): 173–179. Bibcode:1981JSP....26..173G. doi:10.1007/BF01106792.
- ^ Jakobson, M.,"Absolutely continuous invariant measures for one-parameter families of one-dimensional maps," Communications in Mathematical Physics 81, 1981, 39-88.
- ^ 9.0 9.1 : Schröder, Ernst. Über iterierte Funktionen. Math. Ann. 1870, 3 (2): 296–322. doi:10.1007/BF01443992.
- ^ Little, M.; Heesch, D. Chaotic root-finding for a small class of polynomials (PDF). Journal of Difference Equations and Applications. 2004, 10 (11): 949–953. doi:10.1080/10236190412331285351. 已忽略未知参数
|author-separator=(帮助)[永久失效連結] - ^ Lorenz, Edward (1964), "The problem of deducing the climate from the governing equations," Tellus 16 (February): 1-11.
- ^ Veritasium. 这个方程会改变你的世界观. bilibili. 事件发生在 8:37. 2022-02-02 [2022-10-25]. (原始内容存档于2022-10-26) (英语).
教科書[编辑]
- Sprott, Julien Clinton. Chaos and Time-Series Analysis. Oxford University Press. 2003. ISBN 0-19-850840-9.
- Strogatz, Steven. Nonlinear Dynamics and Chaos. Perseus Publishing. 2000. ISBN 0-7382-0453-6.
- Tufillaro, Nicholas; Tyler Abbott, Jeremiah Reilly. An experimental approach to nonlinear dynamics and chaos. Addison-Wesley New York. 1992. ISBN 0-201-55441-0.
外部連結[编辑]
- 曼德博集合和單峰映射的聯繫
- The Chaos Hypertextbook(页面存档备份,存于互联网档案馆)
- Java Applet
- Logistic Map Simulation(页面存档备份,存于互联网档案馆). A Java applet simulating the Logistic Map by Yuval Baror.
- Logistic Map. Contains an interactive computer simulation of the logistic map.
- The Chaos Hypertextbook(页面存档备份,存于互联网档案馆). An introductory primer on chaos and fractals.
- Interactive Logistic map with iteration and bifurcation diagrams in Java.
- Interactive Logistic map showing fixed points.
- Macintosh Quadratic Map Program (页面存档备份,存于互联网档案馆)
- The transition to Chaos and the Feigenbaum constant(页面存档备份,存于互联网档案馆)- JAVA applet
- The Logistic Map and Chaos(页面存档备份,存于互联网档案馆) by Elmer G. Wiens
- Complexity & Chaos (audiobook) by Roger White. Chapter 5 covers the Logistic Equation.
- "History of iterated maps(页面存档备份,存于互联网档案馆)," in 一种新科学 by 史蒂芬·沃爾夫勒姆. Champaign, IL: Wolfram Media, p. 918, 2002.
- Discrete Logistic Equation(页面存档备份,存于互联网档案馆) by Marek Bodnar after work by Phil Ramsden, Wolfram 演示项目.
- Multiplicative coupling of 2 logistic maps(页面存档备份,存于互联网档案馆) by C. Pellicer-Lostao and R. Lopez-Ruiz after work by Ed Pegg Jr, Wolfram 演示项目.
- Using SAGE to investigate the discrete logistic equation(页面存档备份,存于互联网档案馆)
| |||||||||||||||||||||||||||||||||||||||||||||||||



























