普里姆算法

普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克发现；并在1957年由美国计算机科学家罗伯特·普里姆独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

描述

从单一顶点开始，普里姆算法按照以下步骤逐步扩大树中所含顶点的数目，直到遍及连通图的所有顶点。

1. 输入：一个加权连通图，其中顶点集合为V，边集合为E；
2. 初始化：V_new = {x}，其中x为集合V中的任一节点（起始点），E_new = {}；
3. 重复下列操作，直到V_new = V：
   1. 在集合E中选取权值最小的边（u, v），其中u为集合V_new中的元素，而v则不是（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；
   2. 将v加入集合V_new中，将（u, v）加入集合E_new中；
4. 输出：使用集合V_new和E_new来描述所得到的最小生成树。

时间复杂度

最小边、权的数据结构	时间复杂度（总计）
邻接矩阵、搜索	O(V2)
二叉堆（后文伪代码中使用的数据结构）、邻接表	O((V + E) log(V)) = O(E log(V))
斐波那契堆、邻接表	O(E + V log(V))

通过邻接矩阵图表示的简易实现中，找到所有最小权边共需O（V²）的运行时间。使用简单的二叉堆与邻接表来表示的话，普里姆算法的运行时间则可缩减为O(E log V)，其中E为连通图的边数，V为顶点数。如果使用较为复杂的斐波那契堆，则可将运行时间进一步缩短为O(E + V log V)，这在连通图足够密集时（当E满足Ω（V log V）条件时），可较显著地提高运行速度。

例示

图例	说明	不可选	可选	已选
	此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
	顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
	下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
	算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
	在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
	这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
	顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C
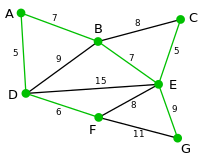
	现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。	无	无	A, D, F, B, E, C, G

证明

设prim生成的树为G₀

假设存在G_min使得cost(G_min)<cost(G₀)

则在G_min中存在(u,v)不属于G₀

将(u,v)加入G₀中可得一个环，且(u,v)不是该环的最长边

这与prim每次生成最短边矛盾

故假设不成立，得证.

Pascal語言程序

部分主程序段：

procedure prim(v0:integer);
var
   lowcost,closest:array[1..maxn] of integer;
   i,j,k,min,ans:integer;
begin
   for i:=1 to n do
    begin
     lowcost[i]:=cost[v0,i];
     closest[i]:=v0;
   end;
   for i:=1 to n-1 do
     begin
      min:=maxint;
      for j:=1 to n do
         if (lowcost[j]<min) and (lowcost[j]<>0) then
          begin
            min:=lowcost[j];
            k:=j;
         end;
      inc(ans, lowcost[k]);
      lowcost[k]:=0;
      for j:=1 to n do
         if cost[k,j]<lowcost[j] then
          begin
            lowcost[j]:=cost[k,j];
            closest[j]:=k;
         end;
   end;
 writeln(ans);
end;

//c语言代码

int lowcost[MAXN],closest[MAXN];
int prim(int v0)
{
    int i,j,mindis,minone;
    int ans = 0;/*用来记录最小生成树的总长度*/
    /*各点距离初始化*/
    for(i = 0;i < n;i++)
    {
        lowcost[i] = cost[v0][i];
        closest[i] = v0;
    }
    for(i = 0;i < n-1;i++)
    {
        mindis = UPPERDIS;
        for(j = 0;j < n;j++)
          if(lowcost[j] && mindis > lowcost[j])
          {
              mindis = lowcost[j];
              minone = j;
          }
        /*将找到的最近点加入最小生成树*/
        ans += lowcost[minone];
        lowcost[minone] = 0;
        /*修正其他点到最小生成树的距离*/
        for(j = 0;j < n;j++)
          if(cost[j][minone] < lowcost[j])
          {
              lowcost[j] = cost[j][minone];
              closest[j] = minone;
          }
    }
    return ans;
}

Java语言实现

import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
 
public class Prim {
 
        public static List<Vertex> vertexList = new ArrayList<Vertex>();//结点集
        public static List<Edge> EdgeQueue = new ArrayList<Edge>();//边集
        public static List<Vertex> newVertex = new ArrayList<Vertex>();//已经 访问过的结点
 
        public static void main(String[] args) {
                primTree();
 
        }
        public static void buildGraph() {
                Vertex v1 = new Vertex("a");
                Prim.vertexList.add(v1);
                Vertex v2 = new Vertex("b");
                Prim.vertexList.add(v2);
                Vertex v3 = new Vertex("c");
                Prim.vertexList.add(v3);
                Vertex v4 = new Vertex("d");
                Prim.vertexList.add(v4);
                Vertex v5 = new Vertex("e");
                Prim.vertexList.add(v5);
                addEdge(v1, v2, 6);
                addEdge(v1, v3, 7);
                addEdge(v2, v3, 8);
                addEdge(v2, v5, 4);
                addEdge(v2, v4, 5);
                addEdge(v3, v4, 3);
                addEdge(v3, v5, 9);
                addEdge(v5, v4, 7);
                addEdge(v5, v1, 2);
                addEdge(v4, v2, 2);
        }
        public static void addEdge(Vertex a, Vertex b, int w) {
                Edge e = new Edge(a, b, w);
                Prim.EdgeQueue.add(e);
        }
        public static void primTree(){
                buildGraph();
                Vertex start = vertexList.get(0);
                newVertex.add(start);
                for(int n=0;n<vertexList.size();n++){
                        Vertex temp = new Vertex(start.key);
                        Edge tempedge = new Edge(start,start,1000);
                        for(Vertex v : newVertex){
                                for(Edge e : EdgeQueue){
                                        if(e.start==v && !containVertex(e.end)){
                                                if(e.key<tempedge.key){
                                                        temp = e.end;
                                                        tempedge = e;
                                                }
 
 
                                        }
                                }
                        }
                        newVertex.add(temp);
                }
                Iterator it = newVertex.iterator();
                while(it.hasNext()){
                        Vertex v =(Vertex) it.next();
                        System.out.println(v.key);
                }
        }
        public static boolean containVertex(Vertex vte){
                for(Vertex v : newVertex){
                        if(v.key.equals(vte.key))
                                return true;
                }
                return false;
        }
}
class Vertex {
        String key;
        Vertex(String key){
                this.key = key;
        }
}
 
class Edge{
        Vertex start;
        Vertex end;
        int key;
        Edge(Vertex start,Vertex end,int key){
                this.start = start;
                this.end  = end;
                this.key = key;
 
        }
}

參考

普林演算法與迪科斯彻演算法的策略相似。