聽出鼓的形狀

這兩塊理想鼓膜發出的聲音一樣，但其形狀不同。 所謂聲音一樣，意思是其具有相同的特徵頻率，因此敲擊發出的音色將具有相同的泛音。此例子由下文的戈登、韋伯，以及沃爾珀特給出。留意兩個多邊形具有相同的面積和周長

從鼓的音色（即其泛音列），利用數學理論，來獲取鼓膜形狀的信息，謂之聽出鼓的形狀。美國數學月刊於1966年刊登了馬克·卡克的論文〈能否聽出鼓的形狀？〉，文題由利普曼·伯斯給出。此數學問題可回溯至赫尔曼·外尔。

卡克1966年的論文使此問題廣為人知。他因為該論文於1967年獲萊斯特·福特獎，並於1968年獲肖夫內獎。

鼓膜可以振動的頻率取決於其形狀。假若已知形狀，則可用亥姆霍兹方程求出頻率。該些頻率為空間（鼓膜）上的拉普拉斯算子的特征值。問題是單由該些頻率是否能確定鼓膜的形狀。例如，沒有其他形狀的鼓膜與正方形鼓膜有相同的泛音列。卡克未能得知是否存在兩個不同的形狀，其具有相同的泛音列。結果，在1992年，戈登、韋伯，以及沃爾珀特證得頻率不能完全決定形狀，解決了原來的問題。

正式敍述

更正式地，鼓視為邊界鉗緊的彈性膜，數學上表示成平面上的一個區域 D. 設 λ_n 為其狄利克雷特徵值：即以下拉普拉斯算子的狄利克雷問題

${\begin{cases}\Delta u+\lambda u=0\\u|_{\partial D}=0\end{cases}}$

的特徵值。兩個區域若具有完全相同的特徵根列，則稱其等譜，或同音（英語：homophonic）。稱為「同音」的原因是，該些狄利克雷特徵值恰好是鼓所能發出的基調：其為鉗緊邊界的波動方程的解的傅立葉系數。

於是，可以將問題轉述成：只知 λ_n 之值，可以推導出 D 的何種性質？又或，更具體地，是否有兩個不同形狀但等譜的區域？

也可以從數個不同方向推廣，提出同樣的問題。其一，可將平面換成高維或黎曼流形，考慮其上的拉氏算子的狄利克雷問題。其二，可將拉氏算子換成其他橢圓算子，例如柯西－黎曼算子或狄拉克算子。其三，可考慮狄利克雷條件以外的其他邊界條件，例如諾伊曼邊界條件。相關課題屬於譜幾何的研究。

答案

由一個連續參數給出的一族等譜的鼓

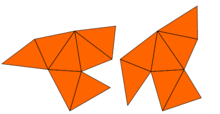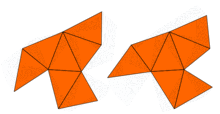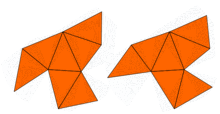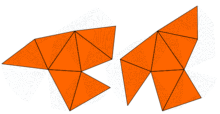
問題提出後，約翰·米爾諾很快觀察到，恩斯特·維特的一條定理足以推出存在兩個不同形狀的 16 維環面，其具有相同的特徵值。然而，原來的二維問題要待1992年才得到解決。當時，卡羅林·戈登 , 大衛·韋伯 (數學家) 和斯科特·沃爾珀特利用砂田方法（得名自砂田利一）, 在平面上構造了兩個不同形狀，但卻具有同樣特徵值的區域。該些區域為凹多邊形。其特徵值相等的證明用到拉氏算子的對稱性。彼得·布塞尔與合作者推廣了此想法，從而構造了若干類似的例子。因此，卡克原先問題的答案是否定的：對於許多形狀，不能完全聽出鼓的形狀，不過仍可推斷出若干性質。

另一方面，史提夫·澤爾迪奇證明，若將卡克的問題收窄到僅考慮邊界解析的平面凸區域，則會得到肯定的答案。仍未知道是否存在兩個非凸的解析區域具有同樣的特徵值，但已知的是，與某個給定區域等譜的所有區域組成的集合，在 C^∞ 拓撲中是緊集。又例如，由鄭氏特徵值比較定理知，球面是譜剛的（英語：spectrally rigid, 即若有流形與之等譜，則其形狀亦必與之相同）。此外，利用奧斯古德（Osgood）、菲利浦斯（Phillips）和薩納克（Sarnak）的成果，可以證明固定虧格的黎曼面組成的模空間中，没有過任何點的連續等譜流，且該模空間在弗雷歇－施瓦茨拓撲（英語：Fréchet–Schwartz topology）下為緊。

外爾公式

主条目：外爾定律

外爾公式斷言，可藉 λ_n 的增長速度推斷鼓的面積 A。定義 N(R) 為小於 R 的特徵值的數目，則可得

$A=\omega _{d}^{-1}(2\pi )^{d}\lim _{R\to \infty }{\frac {N(R)}{R^{d/2}}},\,$

其中 d 是維數，$\omega _{d}$ 是 d-維單位球的體積。外爾猜想迫近式的第二項將給出 D 的周長，即有

$\,N(R)=(2\pi )^{-d}\omega _{d}AR^{d/2}+{\frac {1}{4}}(2\pi )^{-d+1}\omega _{d-1}LR^{(d-1)/2}+o(R^{(d-1)/2}),\,$

其中 L 表示周長（高維情況下則為表面積）。維克托·伊夫里於1980年證明了上式對於某類邊界光滑的流形適用，其不具由兩個連續參數給出的一族測地線（例如球面則具有如此一族測地線）。

外爾－貝里猜想

對於邊界非光滑的情況，邁克爾·貝里於 1979 年猜想，修正值的量級應為

$R^{D/2},\,$

其中 D 為邊界的豪斯多夫維數。寶樂沙 (法語：J. Brossard）和卡莫納（法語：R. A. Carmona）推翻了此猜想，但提出應將豪斯多夫維數改成頂盒維數（即上計盒維數）。在平面上，邊界維數為 1 的情況已獲證（1993 年），但大多數高維情況被否證（1996 年），兩個結論都是拉皮迪和波默蘭斯的成果。

相關條目

• 圓形膜的振動
• 加斯曼三元組
• 等譜
• 譜幾何
• 推廣到疊代函數系統生成的碎形的情況

參考資料

• Abikoff, William, Remembering Lipman Bers (PDF), Notices of the AMS, January 1995, 42 (1): 8–18 [2020-10-04], （原始内容存档 (PDF)于2020-02-07） 
• Brossard, Jean; Carmona, René. Can one hear the dimension of a fractal?. Comm. Math. Phys. 1986, 104 (1): 103–122. Bibcode:1986CMaPh.104..103B. doi:10.1007/BF01210795. 
• Buser, Peter; Conway, John; Doyle, Peter; Semmler, Klaus-Dieter, Some planar isospectral domains, International Mathematics Research Notices, 1994, 9: 391ff 
• Chapman, S.J. Drums that sound the same. American Mathematical Monthly. 1995, 102 (February): 124–138. JSTOR 2975346. doi:10.2307/2975346. 
• Giraud, Olivier; Thas, Koen. Hearing shapes of drums – mathematical and physical aspects of isospectrality. Reviews of Modern Physics. 2010, 82 (3): 2213–2255. Bibcode:2010RvMP...82.2213G. arXiv:1101.1239 . doi:10.1103/RevModPhys.82.2213. 
• Gordon, Carolyn; Webb, David, You can't hear the shape of a drum, American Scientist: 46–55 
• Gordon, C.; Webb, D.; Wolpert, S., Isospectral plane domains and surfaces via Riemannian orbifolds, Inventiones Mathematicae, 1992, 110 (1): 1–22, Bibcode:1992InMat.110....1G, doi:10.1007/BF01231320 
• Ivrii, V. Ja., The second term of the spectral asymptotics for a Laplace–Beltrami operator on manifolds with boundary, Funktsional. Anal. I Prilozhen, 1980, 14 (2): 25–34, doi:10.1007/BF01086550  (In Russian).
• Kac, Mark. Can One Hear the Shape of a Drum? (PDF). American Mathematical Monthly. April 1966, 73 (4, part 2): 1–23 [2020-10-04]. JSTOR 2313748. doi:10.2307/2313748. （原始内容存档 (PDF)于2021-03-02）. 
• Lapidus, Michel L., Can one hear the shape of a fractal drum? Partial resolution of the Weyl–Berry conjecture, Geometric Analysis and Computer Graphics (Berkeley, CA, 1988), Math. Sci. Res. Inst. Publ. (New York: Springer), 1991, 17 (17): 119–126, ISBN 978-1-4613-9713-7, doi:10.1007/978-1-4613-9711-3_13 
• Lapidus, Michel L., Vibrations of fractal drums, the Riemann hypothesis, waves in fractal media, and the Weyl–Berry conjecture, B. D. Sleeman; R. J. Jarvis (编), Ordinary and Partial Differential Equations, Vol IV, Proc. Twelfth Internat. Conf. (Dundee, Scotland,UK, June 1992), Pitman Research Notes in Math. Series 289, London: Longman and Technical: 126–209, 1993 
• Lapidus, M. L.; van Frankenhuysen, M., Fractal Geometry and Number Theory: Complex dimensions of fractal strings and zeros of zeta functions, Boston: Birkhauser, 2000 . (Revised and enlarged second edition to appear in 2005.)
• Lapidus, Michel L.; Pomerance, Carl, The Riemann zeta-function and the one-dimensional Weyl-Berry conjecture for fractal drums, Proc. London Math. Soc., Series 3, 1993, 66 (1): 41–69, doi:10.1112/plms/s3-66.1.41 
• Lapidus, Michel L.; Pomerance, Carl, Counterexamples to the modified Weyl–Berry conjecture on fractal drums, Math. Proc. Cambridge Philos. Soc., 1996, 119 (1): 167–178, Bibcode:1996MPCPS.119..167L, doi:10.1017/S0305004100074053 
• Milnor, John, Eigenvalues of the Laplace operator on certain manifolds, Proceedings of the National Academy of Sciences of the United States of America, 1964, 51 (4): 542ff, Bibcode:1964PNAS...51..542M, PMC 300113 , PMID 16591156, doi:10.1073/pnas.51.4.542 
• Sunada, T., Riemannian coverings and isospectral manifolds, Ann. of Math., 2, 1985, 121 (1): 169–186, JSTOR 1971195, doi:10.2307/1971195 
• Zelditch, S., Spectral determination of analytic bi-axisymmetric plane domains, Geometric and Functional Analysis, 2000, 10 (3): 628–677, arXiv:math/9901005 , doi:10.1007/PL00001633 

外部鏈結

• Isospectral Drums （页面存档备份，存于互联网档案馆） （由特拉華大學的 Toby Driscoll 所寫）
• Some planar isospectral domains （页面存档备份，存于互联网档案馆） by Peter Buser, John Horton Conway, Peter Doyle, and Klaus-Dieter Semmler
• Drums That Sound Alike by Ivars Peterson at the Mathematical Association of America web site
• 埃里克·韦斯坦因. Isospectral Manifolds. MathWorld. 
• Benguria, Rafael D., Dirichlet eigenvalue, Hazewinkel, Michiel (编), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4