克魯斯克爾演算法

克魯斯克爾演算法
概況
類別	最小生成樹
資料結構	併查集
複雜度
平均時間複雜度	$O(|E|\log |V|)$ 或 $O(|E|\alpha (|V|))$
空間複雜度	$O(|E|+|V|)$
相關變數的定義
$V$	點集
$E$	邊集

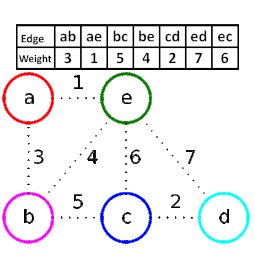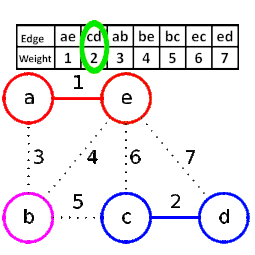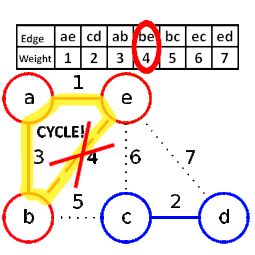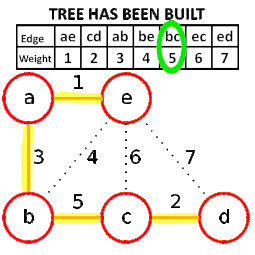
克魯斯克爾演算法（英語：Kruskal's algorithm）是一種用來尋找最小生成樹的演算法，由美國數學家約瑟夫·克魯斯克爾在1956年發表。用來解決同樣問題的還有普林演算法和布盧瓦卡演算法等。三種演算法都是貪婪演算法的應用。和布盧瓦卡演算法不同的地方是，克魯斯克爾演算法在圖中存在相同權值的邊時也有效。

步驟

1. 新建圖$G$，$G$中擁有原圖中相同的節點，但沒有邊
2. 將原圖中所有的邊按權值從小到大排序
3. 從權值最小的邊開始，如果這條邊連接的兩個節點於圖$G$中不在同一個連通分量中，則添加這條邊到圖$G$中
4. 重複3，直至圖$G$中所有的節點都在同一個連通分量中

證明

1. 這樣的步驟保證了選取的每條邊都是橋，因此圖$G$構成一個樹。
2. 為什麽這一定是最小生成樹呢？關鍵還是步驟3中對邊的選取。演算法中總共選取了$n-1$條邊，每條邊在選取的當時，都是連接兩個不同的連通分量的權值最小的邊
3. 要證明這條邊一定屬於最小生成樹，可以用反證法：如果這條邊不在最小生成樹中，它連接的兩個連通分量最終還是要連起來的，通過其他的連法，那麽另一種連法與這條邊一定構成了環，而環中一定有一條權值大於這條邊的邊，用這條邊將其替換掉，圖仍舊保持連通，但總權值減小了。也就是說，如果不選取這條邊，最後構成的生成樹的總權值一定不會是最小的。

時間複雜度

通過使用路徑壓縮的併查集，平均時間複雜度為$O(|E|\log |V|)$，其中$E$和$V$分別是圖的邊集和點集。

此外，如果同時使用路徑壓縮和按秩合併，時間複雜度可以最佳化到 $O(|E|\alpha (|V|))$，其中$\alpha$表示反阿克曼函數。

範例

圖例	說明
	AD和CE是最短的兩條邊，長度為5，其中AD被任意選出，以突顯表示。
	現在CE是不屬於環的最短邊，長度為5，因此第二個以突顯表示。
	下一條邊是長度為6的DF，同樣地以突顯表示。
	接下來的最短邊是AB和BE，長度均為7。AB被任意選中，並以突顯表示。邊BD用紅色突顯表示，因為B和D之間已經存在一條（標為綠色的）路徑，如果選擇它將會構成一個環（ABD）。
	以突顯表示下一條最短邊BE，長度為7。這時更多的邊用紅色突顯標出：會構成環BCE的BC、會構成環DBEA的DE以及會構成環FEBAD的FE。
	最終，標記長度為9的邊EG，得到最小生成樹，結束演算法過程。

虛擬碼

KRUSKAL-FUNCTION(G, w)
1    F := 空集合
2    for each 圖 G 中的頂點 v
3        do 將 v 加入森林 F
4    所有的邊(u, v) ∈ E依權重 w 遞增排序
5    for each 邊(u, v) ∈ E
6        do if u 和 v 不在同一棵子樹
7            then F := F ∪ {(u, v)}
8                將 u 和 v 所在的子樹合併

參考源程式

C++ 實現

以下代碼基於路徑壓縮和按秩合併的併查集，時間複雜度 $O(|E|\alpha (|V|))$。

#include <bits/stdc++.h>

struct DSU {
    std::vector<int> fa, sz;
    DSU(int n = 0) : fa(n), sz(n, 1) {
        std::iota(fa.begin(), fa.end(), 0);
    }
    int Find(int x) { // 路径压缩
        while (x != fa[x])
            x = fa[x] = fa[fa[x]];
        return x;
    }
    bool Merge(int x, int y) { // 按秩合并
        x = Find(x), y = Find(y);
        if (x == y) return false; // 处于同一连通分量
        if (sz[x] > sz[y]) std::swap(x, y);
        fa[x] = y;
        sz[y] += sz[x];
        return true;
    }
}; // 并查集

int main() {
    int n, m; // 点数，边数
    std::cin >> n >> m;
    std::vector<std::tuple<int, int, int>> edge(m);
    // 边集，三元组分别表示边权和边的两个端点
    for (auto &[w, u, v] : edge)
        std::cin >> u >> v >> w;
    std::sort(edge.begin(), edge.end()); // 按边权升序排序
    DSU dsu(n); // 初始化并查集
    long long result = 0; // 最小生成树边权和
    for (auto &[w, u, v] : edge)
        if (dsu.Merge(u, v)) result += w;
        // 合并两个连通分量并统计答案
    std::cout << result << std::endl;
    return 0;
}