格里蝾螈
| 此条目需要更新。 (2019年6月28日) |
| 系列条目 |
| 政治 |
|---|
 |
|
|
格里蝾螈(英语:Gerrymandering)[1],又名不公正划分选区[2],是一个来自美国的政治术语,指以不公平的选区划分方法操纵选举,使投票结果有利于某方。这个术语源自1812年美国马萨诸塞州州长埃尔布里奇·格里(Elbridge Thomas Gerry)将某一选区划分成不寻常的蝾螈(salamander)状,以让民主共和党得胜。当时被重划的选区中,有一选区形状特别怪异,有如蝾螈(一种长得像蜥蜴的两栖动物),格里的政敌于是将格里(Gerry)姓氏与蝾螈的字尾(mander)组合成“gerrymandering”(格里蝾螈),以影射为照顾党派利益,不公平画分选区的方式,此后沿用于世。[3]美国最高法院在1985年裁决该做法违宪,此后各州的众议院选区划分须以人口比例去作分配,而全国则以每十年的人口普查决定州的选区数目。
格里蝾螈的原文“Gerrymander”在其语言的使用方法中,可同时作动词和名词使用。作动词时,指将选区划分成对特定某方有利;作名词时,指专对特定某方利益设计并划分后的选区。其发音方面,原马萨诸塞州州长格里(Gerry)里的“G”是发音成硬G/g/,但在格里蝾螈(gerrymander)里,因为颚化的关系而发音成软G。格里蝾螈常见于实行单一选区制及复数选区制的民主国家。
词源[编辑]

1812年当时美国马萨诸塞州州长埃尔布里奇·格里(Elbridge Thomas Gerry)为确保民主共和党在州议会选举中赢得更多议席,于是签署当时民主共和党凭借州议会多数席次所通过的一项法案,蓄意将马萨诸塞州州议会选区重划,让敌对联邦党人票源集中在少数选区,保障民主共和党候选人能不成比例地当选。尽管有一说称格里对于这样安排党派性很强的选区感到不满,但无论如何他签署该法案而惹议。
当时重划的选区中,有一选区形状相当怪异,状似蝾螈(salamander)的两栖动物;或是传说中亦是长得像蜥蜴的同名怪物沙罗曼达,尾巴长长的,还有翅膀的样子。于是作为其政敌的联邦党便将埃尔布里奇·格里(Gerry)的姓氏与蝾螈的字尾(mander)组合而成“gerrymandering”(格里蝾螈),用来影射为照顾党派利益,不公平划分选区的方式。[4]最后民主共和党赢得该州议员选举,格里本人则输掉州长选举,但随后他成为詹姆斯·麦迪逊的副总统,于1814年任内去世。
操作解说[编辑]

上图为一虚构例子。A至C均有6票红色、9票黑色,A至C的总票数各为15,同时均被划分为三个小区。因应不同的选区划分,双方取得的席位数目截然不同。在A中黑组全取3席,红组0席;在B中,黑组优势被削弱,取得2席,红组取得1席;而在C中,红组却可取得2席,比黑组还要多1席。
手段[编辑]
集中选票和分散选票[编辑]
在选区划分的过程中有两大基本策略,其一是尽可能极大化己方票源的有效使用,其二是尽可能极小化对方票源的有效使用。故此“集中选票”(packing)和“分散选票”(cracking)为格里蝾螈的主要手段。
- “集中选票”指尽可能将敌对阵营支持者集中划入己方的铁票区域,以降低这些选票在其他区域的影响力。亦可将敌对阵营支持者集中特定选区,通过田忌赛马的方式,牺牲这个选区,以降低这些选票在其他区域的影响力,从而保证其他选区己方占优。
- “分散选票”则指尽可能将对方阵营的铁票区域划分成数个选区,以达到稀释对方铁票区域的作用力。
劫持选票和绑架选票[编辑]
另外的方式是针对候选人,包括劫持选票和绑架选票,从而对方阵营受损。
- “劫持选票”通过重新划分两个选区的方式,迫使两位现任者在同一个选区中与对方竞逐,确保其中一位会被除去。[5]
- “绑架选票”将一位现任者的家庭住址放进另一个选区中。[5]如选举规定参选人必需居住在选区之内,更改划界后现任者不再住在其选区中连选会变得更加困难,或者可能面对有着新选民基础的新选区。这常被用作打击代表多个都市区域的政治家,即较大的城区会被从选区中去除,使得选区变得更加乡村。
单一选区制[编辑]
将对方阵营的铁票区域划分成数个选区,使对方无法竞争。
复数选区制[编辑]
除了将对方阵营的铁票区域划分成数个选区,使对方无法竞争。而且划分时使各区人口与应选人比例很大差距,使己方阵营可获得较多席次。
比例代表制[编辑]
划分时使各区人口与应选人比例有很大且不合理的差距,使己方阵营可获得较多席次。例如按照比例代表制分成几个选区,使己方阵营获得较少票数,却能获得相对较多的席次。
各地事例[编辑]
美国[编辑]
美国的国会众议院以及州议会选区划分大致按人口的比例进行选区划分,而各州的众议院选区划分须以人口比例去分配,同时容许各州议会按选举结果去进行选区划分(不是由联邦政府定夺选区)。选区划分使两党制得以巩固,并确保共和党和民主党两大党维持主导地位。
每十年的人口普查及选举结果均会影响未来十年的选区划分,例如在2010年美国中期选举,共和党胜出国会众议院选举,并取得31个州的执政权以及州议会;同年亦是人口普查,该年的选区重划改变选举人票的各州比例,被认为可以确保共和党在未来十年主导美国政治、在选举前占绝对优势,民主党则在加州和纽约州等占绝对优势的地区进行选区划分。选区划分使每两年举行的众议院选举,不少选区实际上在选举举行前已可预知选举结果。这也导致得票和议席不相等的情况,如2018年美国中期选举,共和党在威斯康星州仅取得45%的选票但嬴得63%的议席。
2021年3月22日,自由之家发布特别报告指出,美国的选举制度使得两大党以外的任何第三势力难以成为可行的替代选择,从而为美国越来越严重的政治极化奠定基础;格里蝾螈对美国政治产生了最具腐蚀性和最急剧的影响,意味着立法者可以选择选民,从而使得党内初选成为现任民选官员的真正竞争,而出来投票的通常都是坚定的党派拥护者;这种情况鼓励候选人采取更极端立场,并逐渐偏离中间路线[6]。
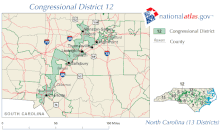
|
北卡罗来纳州第十二国会选区在2003年至2016年间是"集中选票"的一个例子。这个选区中的居民主要是投票给民主党人的非裔美国人。 |
| 加利福尼亚州第二十三国会选区被设计成按比例分割民主党的选民,处于一条狭长的海岸中,是一个"集中选票"式的选区划分例子。该选区在2010年人口普查后由加利福尼亚的无党派委员会重新绘划,不再遵照原有的边界。 | |

|
一个"分散选票"式的选区划分例子。位于地图中央的富兰克林县中,俄亥俄州哥伦布集中的都市(也是主要支持自由派民主党的)区域,被一分为三,每块都被接上主要是投票给共和党的保守派的市郊,且在选票数上被其淹没。 |
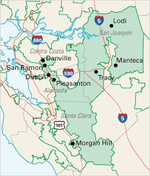
|
加利福尼亚州第十一国会选区被划分成对它当时的现任共和党代表有利。该选区在2010年人口普查后被重划。 |
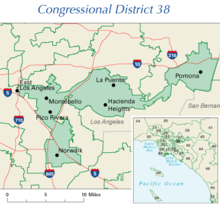
|
两党现任者格里蝾螈制造了加利福尼亚州第三十八国会选区,民主党人Grace Napolitano的在地选区,她在2004年选举中自动当选。该选区在2010年人口普查后由加利福尼亚的无党派委员会重划。 |

|
得克萨斯州在2003年争议性的划分选区使共和党人汤·德利在第22号选区当选。 |

|
加州参议院选区在南加州的怪异形状(2008) 招致了杰利蝾螈的批评。 |
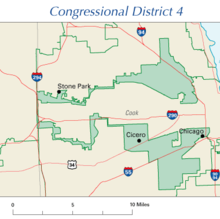
|
伊利诺伊州第四国会选区耳罩般的形状将两块西班牙裔区域集中起来,只在294号州际公路沿线保留狭窄的联结。 |
|
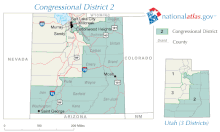
自从民主党人吉姆·马特森在2000年当选后,犹他州立法院重划了第二国会选区以扶助未来的共和党多数地位。主要支持民主党的盐湖城,被与主要支持共和党的犹他州东部和南部通过一条穿过犹他县的狭长地带连接起来。尽管如此,马特森仍然连任。2011年,立法院创建了新的国会选区,将保守的乡村地区与更加都市的区域合并来冲淡民主党选票。 |

|
在州西部的伊利诺伊州第十七国会选区被格里蝾螈,主要的都市中心被联结起来,且迪凯特被包含在内,虽然它几乎与主要选区相分离。2013年被重划。 |
 |
在2014年,华盛顿邮报将马里兰州第三国会选区列入全美前十个杰利蝾螈现象最严重的州。[7] 选区划分偏向民主党人。当前马里兰州第三选区代表约翰·萨班斯提议的关于美国选举改革的For the People Act of 2019即着眼于杰利蝾螈,选举权利和其他问题。[8][9] |
 |
北卡罗来纳州第四国会选区划分不当[7] 2017年被重划。 |
英国[编辑]
英国下议院除了重新划分选区之外,还可透过迁移选民的方法,将己方支持者大量纳入对自己有利的固有选区中,细小选区划分使两党制得以巩固,并确保保守党和工党两大党维持议会的主导地位。选区划分使五年内举行的下议院选举,不少选区在选举举行前已可预知选举结果,大选中逾五百席期分别被保守党及工党占有。
这案例发生在1990年代的英国西敏市,当时保守党执政的地方政府,市议会主席雪莉·波特(Dame Shirley Porter)和其他市议员策划并执行了一个社区政策,将该市内的公共房屋出售给有意支持该党的人民,以支援保守党的边缘选区,使保守党赢得1990年西敏市市议会选举。其后因人口不寻常流动使其他议员及反对阵营有所怀疑,并告上法庭要求审核该社区政策是否合法,雪莉及其余5人最终被判有罪。
爱尔兰[编辑]
1980年代以前,爱尔兰的选区划分方案并非由一个独立委员会负责,而是由政府内部直接决定。故此早期当权的政治人物被抨击是利用格里蝾螈而得益。1947年,爱尔兰由共和党执政,但新兴政党Clann na Poblachta迅速崛起形成威胁。当时的埃蒙·迪·华理拉政府提出《1947年选举法(修正案)》,将选区从138个增加到147个。接下来1948年2月的大选中,Clann na Poblachta只取得了10个议席,与他们获得的得票率不成比例。[10]
1970年代中,地方政府部长詹姆斯·塔利(James Tully)企图将选区重新划分,以确保统一党(Fine Gael)和工党(Labour Party)组成的执政联盟能赢得议会多数。可惜策略失败,执政党最终输掉1977年的大选。事后出现塔利蝾螈(Tullymandering)一词,意指失败版本的格里蝾螈(gerrymandering)。
加拿大[编辑]
2006年加拿大爱德华王子岛省政府决定放弃采用由独立委员会起草的选举地图;相反执政党党团自行设计并采纳了新的选区划分计划,从而引起争议。反对党及媒体皆抨击省长使用格里蝾螈,以操纵选举结果。与此同时,政府所采用的划分方案,确保现任立法议会的执政党党员都能分配到一个小区去竞选连任。尽管如此,20名现任党员中只有7名能于2007年选举中再次当选。[11]
马来西亚[编辑]
自从1957年独立以来,马来西亚国内一直存在着杰利蝾螈的做法。执政联盟(国阵)被指控通过选举委员会修改选区边界来巩固政权。自1974年以来,透过不合理分配制度,当时的霹雳州最多选民人数的议席是最少选民人数的议席的十几倍。[12]2013年选举,国阵尽管普选票只有47%,却获得马来西亚下议院60%的席位。[13]在2018年的选区划分中,杰利蝾螈变得更加严重,尤其以雪兰莪和吉隆坡为最,有统计指执政党最少只需要16.5%的普选票就可执政。[14]
自反对党(即民联)执政马来西亚雪兰莪后(吉隆坡的外围州属)后,马来西亚选举委员会通过重新划分选区以帮助执政党通过分散选票(如图)或集中选票(如位于雪兰莪,全国最大的白沙罗选区拥有超过15万选民,和约百公里以外的全国最小选区布城相比是它的6倍)。重新划分后的选区使得城市凝聚力式微。其中图中加影(Kajang)选区将加影市的大部分地区划入一区,和无拉港(Balakong)及双溪拉玛(Sungai Ramal)属于万宜国会选区。而杜顺大(Dusun Tua)和士毛月(Semenyih)则为加影外围乡村地区,并同时属乌鲁冷岳国会选区,而再划分之前加影属于此选区。这样做使得以城市选票为主的反对党只能赢得左边的万宜,而右边的乌鲁冷岳则很有可能由执政党国阵赢得,除非乡村选民转变支持反对党。不过在2018年大选,反对党希望联盟凭借约五分之一的马来选民票转移反对党,使得杰利蝾螈无法发挥效用。

新加坡[编辑]
几十年来,批评者指责执政人民行动党(PAP)采取包括格里蝾螈的不公平选举做法,以维持新加坡议会的多数席位。[15]当中选举署是新加坡总理领导下的行政部门的一部分,而不是一个独立的机构。[16]批评者指责它赋予执政党权力,根据以往选举结果,辅以选举工程来决定投票区和投票地点。[17]
反对党成员声称,集选区制是“选区划分的同义词”,并指出在反对党在选举中获得比其他选区高的得票率后,选举部门便在下届选举拆散静山集选区和友诺士集选区,并将选民重新分配到其他选区。[18]
菲律宾[编辑]
菲律宾的选区最初是根据1987年宪法委员会制定的《菲律宾宪法》而划分的,但宪法亦同时赋予菲律宾国会有重新划分选区的权力。一旦一个地方的居民数目达到25万,国会便能在这里新增一个选区。这样国会议员通过在新增选区的过程中施加压力,把旧区的人口迁移至目标地区,使该地区成为新的选区。 随着菲律宾人口增加,在1987年最初创立的200个选区之上,又被新增34个选区。以南甘马粦省为例,该省原先只有2个选区,后来被重新划分作3个选区,而其中一个选区事实上未达25万的人口最低要求。[19]这个做法被批评为格里蝾螈,用以使有关政党从中得益。不过菲律宾政党以地方政团为主,因选区数目多,单一政党难以在全国建立势力范围,需要联合执政。
中华民国(台湾)[编辑]
- 新北市立法委员第十二选举区:金山区、万里区与瑞芳区、平溪区、双溪区、贡寮区受基隆市所分隔,仅以汐止区连结两端。
- 台中市立法委员第一选举区:选区内最南的梧栖区,其市区明显距沙鹿市区较近,且依据轮廓及交通易达性综合考量下,应当属第二选区,但因其选举版图结构考量之故被划入第一选区。
- 台中市立法委员第二选举区:跨越屯区及海线地区,仅以乌日区连结两端,两选举区均为形状细长,实际于选区内移动上困难的选区。
- 台中市立法委员第三选举区:后里与神冈、大雅及潭子间,隔了属第八选区的丰原区,且四区中仅后里位于大甲溪以北,且后里市区距其他三区的市区已有逾十公里之遥,而大雅、神冈及潭子,市区最远亦不逾八公里。
中华民国立法委员选举区每十年重划一次,2020年选区重划方案,依据人口增幅民主进步党占有优势的台南市选区增为6席,惟将国民党票源的东区拆分编进2个选区。时任国民党台南市党部主委谢龙介称批评将一个行政区划分为2选区破坏完整性及公平性。[20]
另外的例子,新北市板桥区在2005年的板桥市长选区划分,若照当地的户政事务所采南北向切分区,则东侧选区泛蓝泛绿形成均势;但选区最后采东西向切,使得两选区都变成泛蓝较多的局面。[21]
香港[编辑]
香港区议会全部选区自1994年沿用单议席单票制,选区划分往往引起争议。最典型例子之一是2007年深水埗区议会,重整南昌街一带选区。属于民主派的南昌东选区被一分为四,分划入石硖尾、南昌北、南昌南和南山选区。当中南山选区的新增部分和原有部分其实相隔一座小山。同区的大坑东及又一村选区就分拆,大坑东邨加入原本的南山选区,又一村就加入又一居一带,成为一个纯富有人士的选区,被人质疑以阶级划界。南昌南与南昌中之间的划界甚至细分到以唐楼间的小巷为界。当时的选区划分被不少人质疑别有用心。结果民主派在这一系列改动中失去不少议席,除了“消失”的南昌东一席,还有南昌北和又一村。连民主派本身扎根甚深的南昌中都以些微票数败给亲中候选人,未能重夺因区议员投向民建联而失去的一席,使建制派进入深水埗核心。即使2015年重设的南昌东选区由民主派“取回”,但建制派不单守住2007年夺得的南昌北,更夺得新增人口最多的石硖尾选区,使建制派主导该区议会至2017年。
此后特区政府被在指其他区运用同样手法,意图分割泛民支持较集中的选区来控制增加亲政府议员比例。如2015年的西贡区议会,多个原来泛民议员当选的选区都被重新划区,形成多个选区出现混战。在汲取经验后,特区政府将同样手法用于2019年香港区议会选举,引起现任议员抗议及媒体的关注[22][23]。
2021年4月,随着选举制度改革,重新划分立法会选区[24],部分选区不单打破原有十八区分界,甚至打破传统港九新界分界,将原属新界的离岛区划入香港岛西选区内,引起部分市民质疑[25]。
参见[编辑]
参考文献[编辑]
- ^ Chen, Emily. “杰利蝾螈”如何操纵美国大选. 纽约时报中文网. 2020-06-30 [2024-01-24]. (原始内容存档于2024-01-24).
- ^ gerrymander. 高点法律网 . [2024-01-24]. (原始内容存档于2024-01-24).
- ^ 何謂傑利蠑螈. 联合新闻网. 2016-05-10 [2016-10-19]. (原始内容存档于2020-06-16).
- ^ 避免傑利蠑螈 立委選區重劃是重大考驗. 大纪元. 2005-05-22 [2016-10-19]. (原始内容存档于2020-06-16).
- ^ 5.0 5.1 Pierce, Olga; Larson, Jeff; Beckett, Lois. Redistricting, a Devil’s Dictionary. ProPublica. November 2, 2011 [2017-12-25]. (原始内容存档于2020-12-17).
- ^ 方冰. 自由之家呼吁改善美国民主 “别让专制政权借此妄称他们的制度更优越”. 美国之音中文网. 2021-03-26 [2021-05-29]. (原始内容存档于2021-06-02).
- ^ 7.0 7.1 Ingraham, Christopher. America's most gerrymandered congressional districts. Washington Post. 2014-05-15 [2018-03-29]. ISSN 0190-8286. (原始内容存档于2020-12-03) (美国英语).
- ^ Sarbanes, John. H.R.1 - 116th Congress (2019-2020): To expand Americans' access to the ballot box, reduce the influence of big money in politics, and strengthen ethics rules for public servants, and for other purposes.. www.congress.gov. 2019-01-03 [2019-01-06]. (原始内容存档于2019-01-07).
- ^ 116th Congress (2019). H.R. 1 (116th). Legislation. GovTrack.us. January 3, 2019 [March 7, 2019]. (原始内容存档于2020-12-09).
For the People Act of 2019
- ^ Tim Pat Coogan, De Valera: Long Fellow, Long Shadow (Hutchinson, London, 1993) hardback. page 637 ISBN 0-09-175030-X
- ^ "No Christmas election: Binns". cbc.ca, 16 November 2006. (页面存档备份,存于互联网档案馆)
- ^ Yang Berhomat Dr. Ong, Kiang Ming MP. Malaysia among the most malapportioned countries in the world. 2013-07-19 [2016-02-19]. (原始内容存档于2017-07-02).
- ^ What’s Malay for gerrymandering?. The Economist (Kuala Lumpur). 9 August 2014 [9 November 2014]. (原始内容存档于2018-03-31).
- ^ 净选盟2.0分析选区重划报告·获16.5%普选票可执政. 星洲网. 2018-04-03 [2018-04-22]. (原始内容存档于2018-08-14).
- ^ Channel NewsAsia, "More detailed explanation needed to fend off gerrymandering claims: Analysts", 3 August 2015. http://www.channelnewsasia.com/news/singapore/more-detailed-explanation/2007228.html 互联网档案馆的存档,存档日期28 July 2015.
- ^ Prime Minister's Office, Our Departments 互联网档案馆的存档,存档日期7 June 2008.
- ^ Electoral Engineering: Voting Rules and Political Behavior (页面存档备份,存于互联网档案馆), Pippa Norris
- ^ Lim, Lydia; Hussain, Zakir. Insight: GRCs: 20 years on. Straits Times (Singapore). 2 August 2008 [8 August 2015]. (原始内容存档于2021-03-08).
- ^ Noynoy hits creation of Camarines Sur district for Dato. The Philippine Star. 2010-03-18 [2016-10-19]. (原始内容存档于2017-09-06).
- ^ 南市立委選區劃分 謝龍介痛批:民進黨擺明6席全要. [2018-06-23]. (原始内容存档于2018-04-30).
- ^ 地圖會說話-橫切縱切大不同. [2018-05-04]. (原始内容存档于2018-05-04).
- ^ 彭毅诗, 林景辉. 【政圈風聲】天盛苑反對改劃選區 揭示民建聯實政圓桌新西卡位戰. 香港01. 2018-07-29 [2021-01-16]. (原始内容存档于2020-08-20) (中文(香港)).
- ^ 庄恭南. 【區議會選舉】京士柏選區消失4千人 選管會低估人口有古惑?. 香港01. 2018-07-28 [2021-01-16]. (原始内容存档于2020-08-20) (中文(香港)).
- ^ 修改選舉制度|地方直選新10區分割元朗、沙田、黃大仙. 明报. 2021-04-13 [2021-04-15]. (原始内容存档于2021-04-15) (中文(香港)).
- ^ 梁启智. 討論不值得討論的選區分界. 立场新闻. 2021-04-14 [2021-04-15]. (原始内容存档于2021-04-25) (中文(香港)).
