树 (数据结构)
外观
此条目包含指南或教学内容。 (2016年3月13日) |
此条目没有列出任何参考或来源。 (2016年3月13日) |
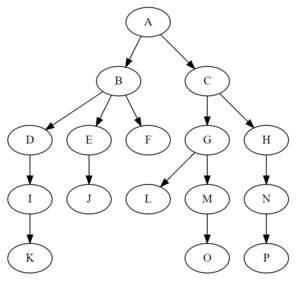
在电脑科学中,树(英语:tree)是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个节点都只有有限个子节点或无子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路(cycle)
术语
[编辑]- 节点的度:一个节点含有的子树的个数称为该节点的度;
- 树的度:一棵树中,最大的节点度称为树的度;
- 叶节点或终端节点:度为零的节点;
- 非终端节点或分支节点:度不为零的节点;
- 父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
- 高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的种类
[编辑]- 有序/无序:
- 无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树。
- 有序树/搜索树/查找树:树中任意节点的子节点之间有顺序关系,这种树称为有序树。即树的所有节点按照一定的顺序排列,这样进行插入、删除、查找时效率就会非常高
- 平衡/不平衡:
- 节点的分叉情况:
- 等叉树:是每个节点的键值个数都相同、子节点个数也都相同
- 不等叉树:每个节点的键值个数不一定相同、子节点个数也不一定相同
- B树:对不等叉树的节点键值数和插入、删除逻辑添加一些特殊的要求,使其能达到绝对平衡的效果。B树全称Balance Tree。如果某个B树上所有节点的分叉数最大值是m,则把这个B数叫做m阶B树。
存储
[编辑]父节点表示法
[编辑]存储结构
[编辑]/* 树节点的定义 */
#define MAX_TREE_SIZE 100
typedef struct
{
TElemType data;
int parent; /* 父节点位置域 */
} PTNode;
typedef struct
{
PTNode nodes[MAX_TREE_SIZE];
int n; /* 节点数 */
} PTree;
|

|
| A |
| ||||||||||||||||||||||||||||||
基本操作
[编辑]设已有链队列类型LinkQueue的定义及基本操作(参见队列)。
构造空树
[编辑]清空或销毁一个树也是同样的操作
void ClearTree(PTree *T)
{
T->n = 0;
}
构造树
[编辑]void CreateTree(PTree *T)
{
LinkQueue q;
QElemType p,qq;
int i=1,j,l;
char c[MAX_TREE_SIZE]; /* 临时存放孩子节点数组 */
InitQueue(&q); /* 初始化队列 */
printf("请输入根节点(字符型,空格为空): ");
scanf("%c%*c",&T->nodes[0].data); /* 根节点序号为0,%*c吃掉回车符 */
if(T->nodes[0].data!=Nil) /* 非空树 */
{
T->nodes[0].parent=-1 ; /* 根节点无父节点 */
qq.name=T->nodes[0].data;
qq.num=0;
EnQueue(&q,qq); /* 入队此节点 */
while(i<MAX_TREE_SIZE&&!QueueEmpty(q)) /* 数组未满且队不空 */
{
DeQueue(&q,&qq); /* 节点加入队列 */
printf("请按长幼顺序输入节点%c的所有孩子: ",qq.name);
gets(c);
l=strlen(c);
for(j=0;j<l;j++)
{
T->nodes[i].data=c[j];
T->nodes[i].parent=qq.num;
p.name=c[j];
p.num=i;
EnQueue(&q,p); /* 入队此节点 */
i++;
}
}
if(i>MAX_TREE_SIZE)
{
printf("节点数超过数组容量\n");
exit(OVERFLOW);
}
T->n=i;
}
else
T->n=0;
}
判断树是否为空
[编辑]Status TreeEmpty(PTree *T)
{ /* 初始条件:树T存在。操作结果:若T为空树,则返回TRUE,否则返回FALSE */
return T->n==0;
}
获取树的深度
[编辑]int TreeDepth(PTree *T)
{ /* 初始条件:树T存在。操作结果:返回T的深度 */
int k,m,def,max=0;
for(k=0;k<T->n;++k)
{
def=1; /* 初始化本节点的深度 */
m=T->nodes[k].parent;
while(m!=-1)
{
m=T->nodes[m].parent;
def++;
}
if(max<def)
max=def;
}
return max; /* 最大深度 */
}
获取根节点
[编辑]TElemType Root(PTree *T)
{ /* 初始条件:树T存在。操作结果:返回T的根 */
int i;
for(i=0;i<T->n;i++)
if(T->nodes[i].parent<0)
return T->nodes[i].data;
return Nil;
}
获取第i个节点的值
[编辑]TElemType Value(PTree *T,int i)
{ /* 初始条件:树T存在,i是树T中节点的序号。操作结果:返回第i个节点的值 */
if(i<T->n)
return T->nodes[i].data;
else
return Nil;
}
改变节点的值
[编辑]Status Assign(PTree *T,TElemType cur_e,TElemType value)
{ /* 初始条件:树T存在,cur_e是树T中节点的值。操作结果:改cur_e为value */
int j;
for(j=0;j<T->n;j++)
{
if(T->nodes[j].data==cur_e)
{
T->nodes[j].data=value;
return OK;
}
}
return ERROR;
}
获取节点的父节点
[编辑]TElemType Parent(PTree *T,TElemType cur_e)
{ /* 初始条件:树T存在,cur_e是T中某个节点 */
/* 操作结果:若cur_e是T的非根节点,则返回它的父节点,否则函数值为"空"*/
int j;
for(j=1;j<T->n;j++) /* 根节点序号为0 */
if(T->nodes[j].data==cur_e)
return T->nodes[T->nodes[j].parent].data;
return Nil;
}
获取节点的最左孩子节点
[编辑]TElemType LeftChild(PTree *T,TElemType cur_e)
{ /* 初始条件:树T存在,cur_e是T中某个节点 */
/* 操作结果:若cur_e是T的非叶子节点,则返回它的最左孩子,否则返回"空"*/
int i,j;
for(i=0;i<T->n;i++)
if(T->nodes[i].data==cur_e) /* 找到cur_e,其序号为i */
break;
for(j=i+1;j<T->n;j++) /* 根据树的构造函数,孩子的序号>其父节点的序号 */
if(T->nodes[j].parent==i) /* 根据树的构造函数,最左孩子(长子)的序号<其它孩子的序号 */
return T->nodes[j].data;
return Nil;
}
获取节点的右兄弟节点
[编辑]TElemType RightSibling(PTree *T,TElemType cur_e)
{ /* 初始条件:树T存在,cur_e是T中某个节点 */
/* 操作结果:若cur_e有右(下一个)兄弟,则返回它的右兄弟,否则返回"空"*/
int i;
for(i=0;i<T->n;i++)
if(T->nodes[i].data==cur_e) /* 找到cur_e,其序号为i */
break;
if(T->nodes[i+1].parent==T->nodes[i].parent)
/* 根据树的构造函数,若cur_e有右兄弟的话则右兄弟紧接其后 */
return T->nodes[i+1].data;
return Nil;
}
输出树
[编辑]void Print(PTree *T)
{ /* 输出树T。加 */
int i;
printf("节点个数=%d\n",T->n);
printf(" 节点 父节点\n");
for(i=0;i<T->n;i++)
{
printf(" %c",Value(T,i)); /* 节点 */
if(T->nodes[i].parent>=0) /* 有父节点 */
printf(" %c",Value(T,T->nodes[i].parent)); /* 父节点 */
printf("\n");
}
}
向树中插入另一棵树
[编辑]Status InsertChild(PTree *T,TElemType p,int i,PTree c)
{ /* 初始条件:树T存在,p是T中某个节点,1≤i≤p所指节点的度+1,非空树c与T不相交 */
/* 操作结果:插入c为T中p节点的第i棵子树 */
int j,k,l,f=1,n=0; /* 设交换标志f的初值为1,p的孩子数n的初值为0 */
PTNode t;
if(!TreeEmpty(T)) /* T不空 */
{
for(j=0;j<T->n;j++) /* 在T中找p的序号 */
if(T->nodes[j].data==p) /* p的序号为j */
break;
l=j+1; /* 如果c是p的第1棵子树,则插在j+1处 */
if(i>1) /* c不是p的第1棵子树 */
{
for(k=j+1;k<T->n;k++) /* 从j+1开始找p的前i-1个孩子 */
if(T->nodes[k].parent==j) /* 当前节点是p的孩子 */
{
n++; /* 孩子数加1 */
if(n==i-1) /* 找到p的第i-1个孩子,其序号为k1 */
break;
}
l=k+1; /* c插在k+1处 */
} /* p的序号为j,c插在l处 */
if(l<T->n) /* 插入点l不在最后 */
for(k=T->n-1;k>=l;k--) /* 依次将序号l以后的节点向后移c.n个位置 */
{
T->nodes[k+c.n]=T->nodes[k];
if(T->nodes[k].parent>=l)
T->nodes[k+c.n].parent+=c.n;
}
for(k=0;k<c.n;k++)
{
T->nodes[l+k].data=c.nodes[k].data; /* 依次将树c的所有节点插于此处 */
T->nodes[l+k].parent=c.nodes[k].parent+l;
}
T->nodes[l].parent=j; /* 树c的根节点的父节点为p */
T->n+=c.n; /* 树T的节点数加c.n个 */
while(f)
{ /* 从插入点之后,将节点仍按层序排列 */
f=0; /* 交换标志置0 */
for(j=l;j<T->n-1;j++)
if(T->nodes[j].parent>T->nodes[j+1].parent)
{/* 如果节点j的父节点排在节点j+1的父节点之后(树没有按层序排列),交换两节点*/
t=T->nodes[j];
T->nodes[j]=T->nodes[j+1];
T->nodes[j+1]=t;
f=1; /* 交换标志置1 */
for(k=j;k<T->n;k++) /* 改变父节点序号 */
if(T->nodes[k].parent==j)
T->nodes[k].parent++; /* 父节点序号改为j+1 */
else if(T->nodes[k].parent==j+1)
T->nodes[k].parent--; /* 父节点序号改为j */
}
}
return OK;
}
else /* 树T不存在 */
return ERROR;
}
删除子树
[编辑]Status deleted[MAX_TREE_SIZE+1]; /* 删除标志数组(全局量) */
void DeleteChild(PTree *T,TElemType p,int i)
{ /* 初始条件:树T存在,p是T中某个节点,1≤i≤p所指节点的度 */
/* 操作结果:删除T中节点p的第i棵子树 */
int j,k,n=0;
LinkQueue q;
QElemType pq,qq;
for(j=0;j<=T->n;j++)
deleted[j]=0; /* 置初值为0(不删除标记) */
pq.name='a'; /* 此成员不用 */
InitQueue(&q); /* 初始化队列 */
for(j=0;j<T->n;j++)
if(T->nodes[j].data==p)
break; /* j为节点p的序号 */
for(k=j+1;k<T->n;k++)
{
if(T->nodes[k].parent==j)
n++;
if(n==i)
break; /* k为p的第i棵子树节点的序号 */
}
if(k<T->n) /* p的第i棵子树节点存在 */
{
n=0;
pq.num=k;
deleted[k]=1; /* 置删除标记 */
n++;
EnQueue(&q,pq);
while(!QueueEmpty(q))
{
DeQueue(&q,&qq);
for(j=qq.num+1;j<T->n;j++)
if(T->nodes[j].parent==qq.num)
{
pq.num=j;
deleted[j]=1; /* 置删除标记 */
n++;
EnQueue(&q,pq);
}
}
for(j=0;j<T->n;j++)
if(deleted[j]==1)
{
for(k=j+1;k<=T->n;k++)
{
deleted[k-1]=deleted[k];
T->nodes[k-1]=T->nodes[k];
if(T->nodes[k].parent>j)
T->nodes[k-1].parent--;
}
j--;
}
T->n-=n; /* n为待删除节点数 */
}
}
层序遍历树
[编辑]void TraverseTree(PTree *T,void(*Visit)(TElemType))
{ /* 初始条件:二叉树T存在,Visit是对节点操作的应用函数 */
/* 操作结果:层序遍历树T,对每个节点调用函数Visit一次且仅一次 */
int i;
for(i=0;i<T->n;i++)
Visit(T->nodes[i].data);
printf("\n");
}
孩子链表表示法
[编辑]存储结构
[编辑]/*树的孩子链表存储表示*/
typedef struct CTNode { // 孩子节点
int child;
struct CTNode *next;
} *ChildPtr;
typedef struct {
ElemType data; // 节点的数据元素
ChildPtr firstchild; // 孩子链表头指针
} CTBox;
typedef struct {
CTBox nodes[MAX_TREE_SIZE];
int n, r; // 节点数和根节点的位置
} CTree;
| A |
| ||||||||||||||||||||||||||||||
森林、树与二叉树的转换
[编辑]见二叉树相应章节
外部链接
[编辑]- (中文)树-数据结构(Python)by EINDEX
- Data Structures and Algorithm Analysis in C (2nd edition) (页面存档备份,存于互联网档案馆)

