任何只包含電壓源、電流源及電阻的黑箱 系統,都可以轉換成諾頓等效電路. 諾頓定理 (英語:Norton's theorem )指的是一個由電壓源 及電阻 所組成的具有兩個端點的電路系統,都可以在電路上等效於由一個理想電流源 I 與一個電阻R 並聯的電路。對於單頻的交流系統,此定理不只適用於電阻,亦可適用於廣義的阻抗 。諾頓等效電路 用來描述線性電源 與阻抗在某個頻率下的等效電路 ,由一個理想電流源與一個理想阻抗並聯組成。
諾頓定理是戴维南定理 的延伸,於1926年由西門子公司 研究員汉斯·费迪南德·迈尔 (Hans Ferdinand Mayer,1895—1980)和貝爾實驗室 工程師爱德华·劳里·诺顿 (1898—1983)分別提出。實際上只有迈尔在此課題上發表過論文,但諾頓只在貝爾實驗室內部用的一份技術報告上提及過他的發現。
諾頓等效電路的計算 [ 编辑 ] 要計算出等效電路,需:
在AB兩端短路(亦即負載電阻為零)的狀況下計算輸出電流I AB 。此為I NO 。
在AB兩端開路(在沒有任何往外電流輸出,亦即當AB點之間的阻抗無限大)的狀況下計算輸出電壓V AB ,此時R No 等於V AB 除以I NO 。 此等效電路是由一個獨立電流I NO 與一個電阻R NO 並聯所組成。 其中的第2項也可以考慮成:
2a.將原始電路系統中的獨立電壓源以短路取代,而且將獨立電流源以開路取代。
2b.若電路系統中沒有非獨立電源的話,則R No 為移走所有獨立電源後的電阻* 。 * 注意:判斷諾頓阻抗大小時,一個更普遍的方法是把電流源連接到電流為一安培的輸出終端,並計算終端的電壓。當電源為非獨立時,這個方法是一定要用的。本法並沒有在下圖中出現。
轉換至戴維寧等效電路 [ 编辑 ] 右圖中,左邊是諾頓等效電路,右邊是戴維寧等效電路 ,可用下列方程式將諾頓等效電路轉換成戴維寧等效電路:
R
T
h
=
R
N
o
{\displaystyle R_{Th}=R_{No}\!}
V
T
h
=
I
N
o
R
N
o
{\displaystyle V_{Th}=I_{No}R_{No}\!}
V
T
h
R
T
h
=
I
N
o
{\displaystyle {\frac {V_{Th}}{R_{Th}}}=I_{No}\!}
其中
R
t
h
{\displaystyle R_{th}}
R
N
o
{\displaystyle R_{No}}
V
t
h
{\displaystyle V_{th}}
I
N
o
{\displaystyle I_{No}}
諾頓等效電路的範例 [ 编辑 ]
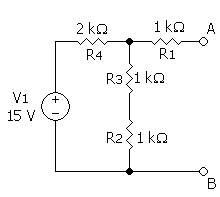
步驟0:原始電路 步驟1:計算等效輸出電流 步驟2:計算等效電阻
步驟3:轉換成等效電路 在此範例中,先將A、B兩點短路,整體電流
I
t
o
t
a
l
{\displaystyle {\boldsymbol {I_{total}}}}
I
t
o
t
a
l
=
15
V
2
k
Ω
+
1
k
Ω
‖
(
1
k
Ω
+
1
k
Ω
)
=
5.625
m
A
{\displaystyle {\boldsymbol {I}}_{\mathrm {total} }={15\mathrm {V} \over 2\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \|(1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega )}=5.625\mathrm {mA} }
利用電流的分流原則,從
R
1
{\displaystyle {\boldsymbol {R_{1}}}}
I
{\displaystyle {\boldsymbol {I_{}}}}
I
=
1
k
Ω
+
1
k
Ω
(
1
k
Ω
+
1
k
Ω
+
1
k
Ω
)
⋅
I
t
o
t
a
l
{\displaystyle {\boldsymbol {I}}={1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \over (1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega )}\cdot I_{\mathrm {total} }}
=
2
3
⋅
5.625
m
A
=
3.75
m
A
{\displaystyle {\boldsymbol {=}}{\frac {2}{3}}\cdot 5.625\mathrm {mA} =3.75\mathrm {mA} }
再把電壓源用短路來取代,從系統開口兩端往裡看的等效阻抗為:
R
=
1
k
Ω
+
2
k
Ω
‖
(
1
k
Ω
+
1
k
Ω
)
=
2
k
Ω
{\displaystyle \ R=1\,\mathrm {k} \Omega +2\,\mathrm {k} \Omega \|(1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega )=2\,\mathrm {k} \Omega }
因此,等效電路則是由一個3.75 mA的電流源並聯一個2KΩ的電阻所組成。
参考资料 [ 编辑 ] 外部連結 [ 编辑 ] 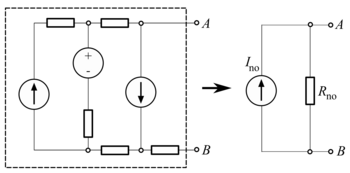



 维基共享资源上的相關多媒體資源:諾頓定理
维基共享资源上的相關多媒體資源:諾頓定理













