图论术语
| 此條目可参照英語維基百科相應條目来扩充。 |
图论中有许多专有名词,此处总结了一些名词的一般意义和用法。
基本术语[编辑]
一个图(一般记作)由两类元素构成,分别称为“顶点”(或节点、结点)和“边”。每条边有两个顶点作为其端点,我们称这条边“连接”了它的两个端点。因此,边可定义为由两个顶点构成的集合(在有向图中为有序对,见下文“方向”一节)。
图也可以用其他模型来表示,如定义在顶点集合上的二元布尔函数,或者方形(0,1)-矩阵。
顶点或边上有标号的图称为有标号的,否则为无标号的。它们的区别在于,无标号的图并没有为顶点或边指定一个特定的顺序。
图的标号一般指按某一规则为图的顶点或边指定一个标号。标号通常是自然数,且一般互不相同。

一个超边是允许连接任意多个(可以多于两个)顶点的“边”。含有超边的“图”称为超图。边可视为恰连接两个顶点的超边,因此图可视为一种特殊的超图。
空图或秃图是没有边的图。
如果一个图有无穷多的顶点和/或边,则称其为无穷的,否则为有穷的。如果一个图是无穷的,但每个顶点的度(见下)是有限的,则称为局部有穷的。一般假定“图”指有穷图。
两个图和,如果存在与之间的一一对应,使得图中两个顶点相连当且仅当它们在图中的对应顶点相连,则称图和 同构,记作。类似地,如果仅仅是到的映射而不一定是一一对应,则称此映射是到的同态。
彼得森图[编辑]
图论中最有名图之一。
边[编辑]
一条边一般表示为连接其两个端点的曲线。以两个顶点、为端点的边一般记作、或。一条边连接两个顶点u、v时,称u与v相邻。图的边集一般记作,当不发生混淆时可简记为。
补图[编辑]
图的补图是这样一的图,它的点集与相同,而每条边存在于中当且仅当它不存在于中。
顶点[编辑]
一个顶点一般表示为一个点或小圆圈。一个图的顶点集(点集)一般记作,当不发生混淆时可简记为。图的阶为其顶点数目,亦即||。
度[编辑]
若两个点之间有一条边,则这两个点相邻。关联一个点的边的条数称为是度数(degree)或价(valency)。特别的,若不是多重图时,它等于这一点的邻点个数。
一个顶点被称作孤立顶点,当它的度数为。
的最小度记为
的最大度记为
的平均度记为
称为k-正则的,当的所有顶点都有相同的顶点度k。特别的,3-正则图被称作立方图。
独立集[编辑]
一個圖的獨立集是圖中一些兩兩不相鄰的頂點所形成的集合。
二分图[编辑]
图G是二分图当且仅当它的点集V能被划分成两块X和Y,使得对于G中的任意一条边,它有一个端点属于X而另一个端点属于Y。
哈密尔顿图[编辑]
环[编辑]
看环(图论)。
结[编辑]
距离[编辑]
距离是两个顶点之间经过最短路径的边的数目,通常用表示。
顶点的偏心率(eccentricity),用来表示连接图中的顶点到图中其它顶点之间的最大距离,用符号表示。
图的直径(diameter),表示取遍图的所有顶点,得到的偏心率的最大值,记作。相对于直径的一个概念是图的半径(radius),表示图的所有点的偏心率的最小值,记作。这两者间的关系是:
柯尼斯堡七桥问题[编辑]
图论中著名的问题。
立方图[编辑]
连通图/连通性[编辑]
称是连通的,如果非空图的任意两个顶点之间均有一条路相连。
称是k-连通的,如果非空图的任意两个顶点之间都有条独立路相连。k-连通的的另外一个定义是:若,且对任意满足的子集均有是连通的,则称是k-连通的。由门格尔定理,易知这两个定义是等价的。通过k-连通的概念,定义使得是k-连通的最大整数称作的连通度。
类似的,还可以引入k-边连通的概念:称一个的图是k-边连通的,如果对任意一个满足的边的集合,均是连通的。同样,的边连通度是使得是k-边连通的最大整数。
旅行推销员问题[编辑]
计算机科学中最有名的问题之一。
欧拉路径[编辑]
匹配[编辑]
平面图[编辑]
库拉托夫斯基定理描述了有点平面图。有名的欧拉公式也说:V-E+F=2. 这是欧拉示性数。
嵌入[编辑]
强连通分量[编辑]
桥[编辑]
路径[编辑]
路径(walk),又译作途径。一个长度为的路径是一个非空的顶点和边的交错序列,使得对于所有均有。特别的,当时,称这个路径是闭的(closed);当路径中的顶点互不相同,得到的一条路。[1]
树[编辑]

连通无圈图称为树,一般记为T。其中,度数为1的顶点称为叶子,否则称为内点。有时我们会从树中选出一个顶点作为特殊顶点,称之为根以示区分,此时称此树为有根树。有根树常作为有向无环图来处理。
树T的连通子图称为T的子树。
树也是一个团的森林。
森林[编辑]
无环(不一定连通)图称为森林,森林F的子图称为F的子森林。
如果图G的一个生成子图是树,则称该子图为生成树。
星是仅有一个顶点不是叶子的树。星也可以表示为完全二分图K1,n。
缩图[编辑]
随机图[编辑]
团[编辑]
图中的团是由图中两两相邻的顶点构成的集合。
Utility graph[编辑]
完全图[编辑]
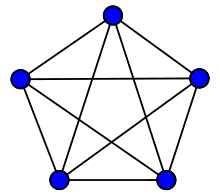
完全图是所有顶点两两相邻的图。n阶完全图,记作Kn。如图所示为K5。n阶完全图有n(n-1)/2条边。
网络流[编辑]
重要的计算机科学、最优化理论、与算法学的题目。也看最大流最小割定理。
围长[编辑]
圍長定義為圖所包含的最短環長,也被称为"girth"。
线图[编辑]
相邻[编辑]
兩頂點相鄰,意思是之間有一條邊。
叶子[编辑]
看以上的树术语。
正则图[编辑]
自环[编辑]
一个自环是两个端点为同一顶点的边。如果有多于一条边连接同一对顶点,则它们均被称为重边。一个图的重数是重复次数最多的边的重复次数。如果一个图不含自环或重边,则称为简单图。多数情况下,如无特殊说明,可以假定“图”总是指简单图。
着色[编辑]
图着色问题包含四色定理,数学中最有名的问题之一。现代的证明用电脑、文章很长。
子图[编辑]
两个图G和H,如果V(H)是V(G)的子集且E(H)是E(G)的子集(当然,E(H)中只能包含将V(H)中的顶点相连的边)则称H是G的子图。如果图G和H不相等,即V(H)是V(G)的真子集或E(H)是E(G)的真子集,则称H是G的真子图。如果H是G的子图或者存在一个G的子图与H同构,则称G包含H。
如果图G的子图H满足V(H)=V(G),即图H包含图G的所有顶点,则称H是G的支撑子图或生成子图。
如果图G的子图H满足边(u,v)在图H中当且仅当边(u,v)在图G中,即图H包含了图G中所有两个端点都在V(H)中的边,则称H是G的导出子图。
对于图的某个性质而言,如果图G具有此性质而G的任一真子图都不具有此性质,则称G是具有该性质的极小图。类似地,如果图G具有此性质而任一以G为真子图的图都不具有此性质,则称G是具有该性质的极大图。
最短路问题[编辑]
重要的计算机科学、与算法学的题目。也看Dijkstra算法、Kruskal算法、等。
定理术语[编辑]
- 彼得森定理
- 布鲁克斯定理
- 柯尼格引理
- 柯尼格定理 (圖論)
- 库拉托夫斯基定理
- 拉姆齐定理(而且看拉姆齐理论)
- 门格尔定理(Menger's Theorem)
- 图特定理
- Vizing定理
- 最大流最小割定理
图的方向[编辑]
有向无环图[编辑]
代数图论[编辑]
不变量[编辑]
亏格(几何、拓扑)[编辑]
看以上的平面图。
譜圖論[编辑]
参考来源[编辑]
- ^ R.Diestel. 图论 第四版. 高等教育出版社. : 10.
参见[编辑]
- 图
- 图论
- 图论话题列表
- 数学
- 离散数学
- 组合数学
- 算法
- 计算机科学
- 最优化
- 人工智能(神经网格)
- 连接组(承现峻,connectome)
- 网格科学
- 费曼图(Feynman diagram、物理、量子力学、统计力学)
| ||||||||||||||||||||||||||||||||||||||||||||||




































