正十六胞体
| 正十六胞体 (16胞体) | |
|---|---|
 | |
| 類型 | 正多胞体 |
| 家族 | 正轴形、超半方形 |
| 對偶多胞形 | 四維超正方體 |
| 識別 | |
| 鮑爾斯縮寫 | hex |
| 數學表示法 | |
| 考克斯特符號 | |
| 施萊夫利符號 | {3,3,4} |
| 性質 | |
| 胞 | 16 (3.3.3) |
| 面 | 32 {3} |
| 邊 | 24 |
| 頂點 | 8 |
| 組成與佈局 | |
| 顶点图 |  (3.3.3.3) |
| 對稱性 | |
| 對稱群 | C4, [3,3,4] |
| 特性 | |
| 凸、等角、等邊、等面 | |
正十六胞体(Hexadecachoron)是数学家施莱夫利最先发现的六个四维凸正多胞体之一。它是四维的正轴形,是二维正方形、三维正八面体的类比。同时,它还是四维的半超方形,即半超正方体。
几何
[编辑]正十六胞体由十六个正四面体胞组成。其24条棱组成6个在不同坐标平面的正方形,它们互相正交;也能组成4个在不同三维超平面上的正八面体,也互相正交。
作为四维正轴形,正十六胞体的八个顶点坐标是
(±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1)。
它的二胞角是120°,可知其能独自完成四维超空间堆砌,称为正十六胞体堆砌,施莱夫利符号{3,3,4,3}。它由16个正四面体胞、32个正三角形面、24条棱、8个顶点组成,棱图是正方形,顶点图是正八面体。对于边长为a的正十六胞体,其超体积为,表体积是。
对于边长为a的正十六胞体,其外接超球半径为,外中交超球(经过正十六胞体各边中点的四维超球)半径为,内中交超球(经过正十六胞体各面中心的四维超球)半径为,内切超球半径为。
对称群构造
[编辑]作为四维正轴形,它具有C4对称群,但它同时也是四维的半超方形(可看作以一定规律选取超方形一半的顶点构成新的半正多胞形,见交错),对应施莱夫利符号h{4,3,3},考斯特标记![]()
![]()
![]()
![]()
![]()
![]()
![]() 或
或![]()
![]()
![]()
![]()
![]() ,具有更低的对称性。也可把它看作正四面体反棱柱,即由两个以对偶形式存在的互相平行的正四面体和链接它们顶点和面的正四面体组成,施莱夫利符号h0,1{2,4,3}其对称性更低。也因为其对偶超立方体是四角四角柱體柱,它也是四角四角錐體錐,而由于它又是超立方体的交错,它也是四角四角反柱體反柱,施莱夫利符号{4}+{4}。更多对称群见下表:
,具有更低的对称性。也可把它看作正四面体反棱柱,即由两个以对偶形式存在的互相平行的正四面体和链接它们顶点和面的正四面体组成,施莱夫利符号h0,1{2,4,3}其对称性更低。也因为其对偶超立方体是四角四角柱體柱,它也是四角四角錐體錐,而由于它又是超立方体的交错,它也是四角四角反柱體反柱,施莱夫利符号{4}+{4}。更多对称群见下表:
| 对应名称 | 考克斯特符号 | 施莱夫利符号 | 对称性 | 群阶 | 顶点图 |
|---|---|---|---|---|---|
| 正十六胞体 | {3,3,4} | [3,3,4] | 384 | ||
| 半超正方体 | h{4,3,3} {3,31,1} |
[31,1,1] = [1+,4,3,3] | 192 | ||
| 四角四角錐體錐 | {4}+{4} | [[4,2,4]] | 128 | ||
| 交错四角四角柱體柱 | 2s{4,2,4} | [[4,2+,4]] | 64 | ||
| 正四面体反棱柱 | s{2,4,3} | [3,4,2+] | 48 | ||
| 交错四角柱體柱 | [4,2+,4] | 32 | |||
| 交错正方形棱柱棱柱 | sr{2,2,4} | [4,(2,2)+] | 16 | ||
| 扭棱四维超矩形 | s{21,1,1} | [23]+ | 8 | ||
| 4-长菱体 | |||||
| {3,3,4} | [3,3,4] | 384 | |||
| {4}+{4} | [[4,2,4]] | 128 | |||
| {3,4}+{} | [4,3,2] | 96 | |||
| {4}+{}+{} | [4,2,2] | 32 | |||
| {}+{}+{}+{} | [2,2,2] | 16 |
可视化
[编辑]| 球极投影 | 展开图(这里显示了正十六胞体作为 不同家族的两种展开图,左边的是 正轴形,右边是半立方形,两种 不同颜色的胞“意义”不同) |
单旋转着的透视投影 |
|---|---|---|
 |
 |

|
| 考克斯特平面 | B4 | B3 / D4 / A2 | B2 / D3 |
|---|---|---|---|
| 图像 | 
|

|

|
| 二面体对称群 | [8] | [6] | [4] |
| 考克斯特平面 | F4 | A3 | |
| 图像 | 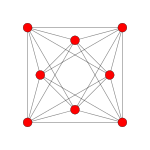
|
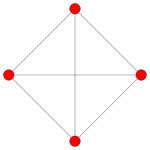
| |
| 二面体对称群 | [12/3] | [4] |
 在4阶皮特里多边形对称性中的截半超正方体,也作为交错超正方体 |
 四维超正方体 |
密铺
[编辑]
正十六胞体可以獨立密铺四维欧氏空间,这个密铺被叫做正十六胞体堆砌,有施莱夫利符号{3,3,4,3},它的对偶四维砌——正二十四胞体堆砌,{3,4,3,3},是正二十四胞体的四维欧氏空间密铺。再加上超正方体堆砌,{4,3,3,4},这就是四维欧几里得空间R4中唯一的3个凸正密铺。每个正十六胞体都与16个相邻的正十六胞体四维胞共用一个四面体胞,与24个相邻的四维胞共用一条棱,与72个相邻的四维胞共用一个顶点。每个顶点处都有24个正十六胞体相交,因此,正十六胞体堆砌的顶点图是正十二胞体。
投影
[编辑]
正十六胞体到三维的正对胞的平行投影有着立方体形的凸包,最近的和最远的(从四维视角来看)正四面体胞被投影成了立方体的内接四面体,正好对应于将正四面体内接于立方体的两种不同方式。在每个这样的内接正四面体周围是4个(非正的)四面体,即是与最近的和最远的正四面体胞相邻的正四面体胞的投影,填充了内接正四面体与立方体之间的空隙。剩余的6个胞被投影成了立方体的6个正方形面。在这一投影中,正十六胞体所有的棱都位于投影的凸包上。
正十六胞体到三维的正对胞的透视投影有着三角化正四面体凸包,其内部结构与平行投影相似。
正十六胞体到三维的正对顶点的平行投影有着正八面体形的凸包,正八面体能够被其“坐标平面”划分为8个四面体部分,这里每一个四面体都是远近一对正四面体胞的投影,距离四维视角最远和最近的顶点都被投影成了正八面体的中心。
最后,正十六胞体到三维的正对棱的平行投影有着压扁的八面体的凸包;正对面的平行投影有一个六角双棱锥凸包。
四球维恩图
[编辑]正十六胞体通常的球极投影 和4个相交的球(4个集合的维恩图),在拓扑上是三维空间中的同一物体:
和4个相交的球(4个集合的维恩图),在拓扑上是三维空间中的同一物体:

|
 |
 |
 |

|
参考
[编辑]- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (第三版, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 第三版, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter,F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication参与修改, 1995, ISBN 978-0-471-01003-6 [1] (页面存档备份,存于互联网档案馆)
- (22页) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (23页) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (24页) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (26章.409页: Hemicubes: 1n1)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Regular Convex Four-Dimensional Polytopes 提供了正十六胞体的部分几何数据。
| 四维正多胞体 | |||||
|---|---|---|---|---|---|
| 正五胞体 | 超立方体 | 正十六胞体 | 正二十四胞体 | 正一百二十胞体 | 正六百胞体 |
| {3,3,3} | {4,3,3} | {3,3,4} | {3,4,3} | {5,3,3} | {3,3,5} |






