正十六胞體

正十六胞體 （16胞體）
類型	正多胞體
家族	正軸形、超半方形
對偶多胞形	四維超正方體
識別
鮑爾斯縮寫	hex
數學表示法
考克斯特符號
施萊夫利符號	{3,3,4}
性質
胞	16 (3.3.3)
面	32 {3}
邊	24
頂點	8
組成與佈局
頂點圖	(3.3.3.3)
對稱性
對稱群	C4, [3,3,4]
特性
凸、等角、等邊、等面

正十六胞體（Hexadecachoron）是數學家施萊夫利最先發現的六個四維凸正多胞體之一。它是四維的正軸形，是二維正方形、三維正八面體的類比。同時，它還是四維的半超方形，即半超正方體。

幾何

正十六胞體由十六個正四面體胞組成。其24條棱組成6個在不同坐標平面的正方形，它們互相正交；也能組成4個在不同三維超平面上的正八面體，也互相正交。 作為四維正軸形，正十六胞體的八個頂點坐標是
(±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1)。
它的二胞角是120°，可知其能獨自完成四維超空間堆砌，稱為正十六胞體堆砌，施萊夫利符號{3,3,4,3}。它由16個正四面體胞、32個正三角形面、24條棱、8個頂點組成，棱圖是正方形，頂點圖是正八面體。對於邊長為a的正十六胞體，其超體積為${\frac {a^{4}}{6}}$，表體積是${\frac {4{\sqrt {2}}a^{3}}{3}}$。

對於邊長為a的正十六胞體，其外接超球半徑為${\frac {\sqrt {2}}{2}}\approx 0.7071067812$,外中交超球（經過正十六胞體各邊中點的四維超球）半徑為${\frac {1}{2}}$,內中交超球（經過正十六胞體各面中心的四維超球）半徑為${\frac {\sqrt {6}}{6}}\approx 0.4082482905$,內切超球半徑為${\frac {\sqrt {2}}{4}}\approx 0.3535533906$。

對稱群構造

作為四維正軸形，它具有C₄對稱群，但它同時也是四維的半超方形（可看作以一定規律選取超方形一半的頂點構成新的半正多胞形，見交錯），對應施萊夫利符號h{4,3,3}，考斯特標記或，具有更低的對稱性。也可把它看作正四面體反稜柱，即由兩個以對偶形式存在的互相平行的正四面體和連結它們頂點和面的正四面體組成，施萊夫利符號h_0,1{2,4,3}其對稱性更低。也因為其對偶超立方體是四角四角柱體柱，它也是四角四角錐體錐，而由於它又是超立方體的交錯，它也是四角四角反柱體反柱，施萊夫利符號{4}+{4}。更多對稱群見下表：

對應名稱	考克斯特符號	施萊夫利符號	對稱性	群階	頂點圖
正十六胞體		{3,3,4}	[3,3,4]	384
半超正方體	=	h{4,3,3} {3,31,1}	[31,1,1] = [1+,4,3,3]	192
四角四角錐體錐		{4}+{4}	[[4,2,4]]	128
交錯四角四角柱體柱		2s{4,2,4}	[[4,2+,4]]	64
正四面體反稜柱		s{2,4,3}	[3,4,2+]	48
交錯四角柱體柱			[4,2+,4]	32
交錯正方形稜柱稜柱		sr{2,2,4}	[4,(2,2)+]	16
扭棱四維超矩形		s{21,1,1}	[23]+	8
4-長菱體
		{3,3,4}	[3,3,4]	384
		{4}+{4}	[[4,2,4]]	128
		{3,4}+{}	[4,3,2]	96
		{4}+{}+{}	[4,2,2]	32
		{}+{}+{}+{}	[2,2,2]	16

可視化

球極投影	展開圖（這裏顯示了正十六胞體作為 不同家族的兩種展開圖，左邊的是 正軸形，右邊是半立方形，兩種 不同顏色的胞「意義」不同）	單旋轉着的透視投影

正交投影

考克斯特平面	B4	B3 / D4 / A2	B2 / D3
圖像
二面體對稱群	[8]	[6]	[4]
考克斯特平面	F4	A3
圖像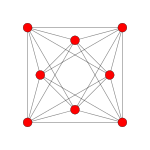
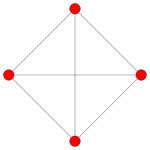
二面體對稱群	[12/3]	[4]

正交投影圖像

在4階皮特里多邊形對稱性中的截半超正方體，也作為交錯超正方體

四維超正方體

密鋪

正十六胞體堆砌

正十六胞體可以獨立密鋪四維歐氏空間，這個密鋪被叫做正十六胞體堆砌，有施萊夫利符號{3,3,4,3}，它的對偶四維砌——正二十四胞體堆砌，{3,4,3,3}，是正二十四胞體的四維歐氏空間密鋪。再加上超正方體堆砌，{4,3,3,4}，這就是四維歐幾里得空間R⁴中唯一的3個凸正密鋪。每個正十六胞體都與16個相鄰的正十六胞體四維胞共用一個四面體胞，與24個相鄰的四維胞共用一條棱，與72個相鄰的四維胞共用一個頂點。每個頂點處都有24個正十六胞體相交，因此，正十六胞體堆砌的頂點圖是正十二胞體。

投影

正十六胞體投影的凸包，不同的胞被塗上了不同的顏色，後半面的胞未畫出。

正十六胞體到三維的正對胞的平行投影有着立方體形的凸包，最近的和最遠的（從四維視角來看）正四面體胞被投影成了立方體的內接四面體，正好對應於將正四面體內接於立方體的兩種不同方式。在每個這樣的內接正四面體周圍是4個（非正的）四面體，即是與最近的和最遠的正四面體胞相鄰的正四面體胞的投影，填充了內接正四面體與立方體之間的空隙。剩餘的6個胞被投影成了立方體的6個正方形面。在這一投影中，正十六胞體所有的棱都位於投影的凸包上。

正十六胞體到三維的正對胞的透視投影有着三角化正四面體凸包，其內部結構與平行投影相似。

正十六胞體到三維的正對頂點的平行投影有着正八面體形的凸包，正八面體能夠被其「坐標平面」劃分為8個四面體部分，這裏每一個四面體都是遠近一對正四面體胞的投影，距離四維視角最遠和最近的頂點都被投影成了正八面體的中心。

最後，正十六胞體到三維的正對棱的平行投影有着壓扁的八面體的凸包；正對面的平行投影有一個六角雙稜錐凸包。

四球溫氏圖

正十六胞體通常的球極投影和4個相交的球（4個集合的溫氏圖），在拓撲上是三維空間中的同一物體：

參考

• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
• H.S.M. Coxeter:
  • Coxeter, Regular Polytopes, (第三版, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • H.S.M. Coxeter, Regular Polytopes, 第三版, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter,F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication參與修改, 1995, ISBN 978-0-471-01003-6 [1] （頁面存檔備份，存於互聯網檔案館）
    • (22頁) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (23頁) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (24頁) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (26章.409頁: Hemicubes: 1_n1)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
• Regular Convex Four-Dimensional Polytopes 提供了正十六胞體的部分幾何數據。

四維正多胞體
正五胞體	超立方體	正十六胞體	正二十四胞體	正一百二十胞體	正六百胞體
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}