均时差

均时差：在轴上方，日晷相对于显示当地平均时间(钟表时)的时钟显示得较快，而在轴下方，日晷显示的时间慢于平太阳时。

此图显示时钟比太阳早 （+） 或晚 （-） 多少分钟。请参阅下文的“表示法”。

均时差（英语：equation of time）描述了两种太阳时间之间的差异。英文的“equation”（方程式）一词用于中世纪时的意义为“差异调和”。这两种不同的时间是视太阳时和平太阳时，前者直接跟踪太阳的周日运动，后者跟踪沿天球赤道以均匀速运动的理论平太阳。视太阳时可以通过量测太阳的当前位置（时角）来获得，如日晷所示（精度有限）。“平”太阳时，对于同一地点，将是由一个稳定的时钟指示的时间，这样在一年中，它与视太阳时的差异将平均为零。

均时差是日行迹的东分量或西分量，这是一条曲线，表示从地球上看太阳在天球上的平均位置的角度偏移。天文学界普遍借由天文台编制的年鉴和星历表将一年中每天的均时差列出

均时差可以近似为两个正弦波的和（见下面的解释）：

$D=6.240\,040\,77+0.017\,201\,97(365.25(y-2000)+d)$

$\Delta t_{ey}=-7.659\sin(D)+9.863\sin \left(2D+3.5932\right)$ [minutes]

此处$d$表示自当年$y$1月1日起的天数。

概念

带有显示均时差辅助表盘的时钟。 那不勒斯的但丁广场（1853）。

在一年中，均时差如图所示变化；它从一年到下一年的变化很小。日晷显示的视太阳时可以提前（快速）多达 16分33秒（约11月3日），或落后（放缓）多达14分6（大约2月11日）。均时差在4月15日、6月13ˋ9月1日和12月25日附近为0。忽略地球轨道和自转的缓慢变化，这些事件每回归年都会在同一时间重复发生。但是，由于一年中的天数是非整数，因此这些日期每年可能会相差一天左右。做为日期不准确的一个例子，根据美国海军天文台的“多年互动式计算机年鉴”（英语：Multiyear Interactive Computer Almanac，MICA），均时差在2011年4月16日为02:00UT1 。

均时差的图形由两条正弦曲线之和近似表示，一条周期为一年，另一条为半年。这些曲线反映了两种天文效应，每种效应都会导致太阳相对于恒星的视运动出现不同的不均匀性：

• 黄道（地球围绕太阳的年轨道运动平面）的倾角，相对于地球赤道平面倾斜约23.44度；和
• 围绕太阳的地球轨道的离心率约为0.0167。

只有当行星的轴向倾角和轨道离心率均为零时，均时差才会消失。行星具有大均时差的两个例子是火星和天王星。在火星上，由于其轨道的离心率相当大，日晷时间和时钟时间之间的差异可能高达50分钟。天王星有一个非常大的轴向倾斜，它有一个均时差，根据它在轨道上的位置，它的日子会提前或延后几个小时开始和结束。

表示法

动画显示了一年内的均时差和日行迹路径。

美国海军天文台指出，“均时差”是“视太阳时”减去“平太阳时”的差值，即如果太阳在时钟前面，则符号为+（正），如果时钟在太阳前面，则标记为-（负）。上图显示了一年多时间的均时差。下图（恰好覆盖一个行事历年）具有相同的绝对值，但符号是相反的，因为它显示了时钟比太阳领先多远。出版品可以使用以下任一格式： 在英语世界，前者的用法更为常见，但并不总是被遵循。任何使用已发布的表或图的人都应该先检查其符号使用情况。通常，会有一个注释或标题来解释它。否则，可以通过知道在每年的前三个月，时钟会早于日晷来确定使用方式。记忆术的“NYSS”（发音为“耐斯”，“英语：new year, sundial slow”），意为“新年，日晷慢”，可能很有用。一些已发布的表格通过不使用符号，而是通过显示“日晷快”（英语：Sundial fast）或“日晷慢”（英语：Sundial slow）等短语来避免歧义。

历史

“均时差”一词来源于中世纪拉丁语“aequātiō diērum”，意思是“日数的程式”（{{|lang-en| equation of days}}）或“日的差异”（英语：difference of days）。 “aequātiō”（和中古英语“equation”）这个字在中世纪天文学中，用于将观测值与期望值之间的差异制成表格（如中心差、二分差、本轮差）。 杰拉尔德·詹姆斯·图默使用源自拉丁语“aequātiō”（均衡或调整）的中世纪术语“equation”，用来表示托勒密的平均太阳时和视太阳时之间的差值。约翰尼斯·开普勒对“equation”的定义是“平均近点角的度数和分钟数与校正尽点角的度数和分钟之间的差值”

视太阳时和平太阳时之间的差异自古以来就被天文学家所认识，但在17世纪中叶精确机械锺发明之前，日晷是唯一可靠的时计，而视太阳时是普遍接受的标准。直到 19 世纪初，平太阳时才取代了国家年历和星历中的视太阳时 。

早期天文学

巴比伦人知道太阳每天不规则的运动。 Handy Tables 托勒密的《天文学大成》第三卷（2世纪）主要关注太阳的异常现象，他在自己的《便条》中列出了均时差。托勒密讨论了将太阳的子午线交点转换为平均太阳时所需的校正，并考虑了太阳沿黄道的非均匀运动和太阳黄道经度的子午线校正。他表示，最大修正值为8+1⁄3时间度或5⁄9小时（第三卷，第9章）。然而，他认为这种影响与大多数计算无关，因为它对缓慢移动的发光体可以忽略不计，只适用于移动最快的发光体：月球。

根据托勒密在《天文学大成》中的讨论，均时差（阿拉伯语“taʿdīl al-ayyām bi layālayhā”）的值是《中世纪伊斯兰天文学》作品中表格（“zij”）的标准值。

近代早期

参见：时差钟

内维尔·马斯基林在1767年的《航海年鉴》中给出了视时间和平均时间的描述：“表观时间是从太阳直接推断出来的时间，无论是从它经过子午线的观察中，还是从观察到的日出或日落中。这个时间不同于陆地上监管良好的钟表所显示的时间，这被称为等值时间或平均时间。”他接着说，在海上，如果观测者需要平均时间，那么通过观测太阳得到的视时间必须通过均时差进行校正。

正确的时间最初被认为是日晷显示的时间。当引入好的机械钟时，它们每年只在四个日期附近与日晷一致，因此使用均时差来“校正”它们的读数以获得日晷时间。一些被称为时差钟的时钟包含一个内部机制来执行这种“校正”。后来，随着时钟成为占主导地位的优质钟表，未经校正的时钟时间，即“平均时间”，成为公认的标准。日晷的读数，当它们被使用时，当时是，而且现在仍然是，用与以前相反的方向使用的均时差进行校正，以获得时钟时间。因此，许多日晷上都刻有均时差的表格或图表，以便用户进行校正。

历史上，均时差被用来设定时钟。从1656年精确时钟的发明到1900年左右商业时间分配服务的出现，陆基时钟有几种常见的设置方法。日晷被读取，并用均时差的表格或图表进行校正。如果有中星仪可以使用，则记录太阳穿过子午线的中天（太阳似乎位于观察者正南或正北的时刻）；然后将时钟设定为正午，并根据该日期的均时差给出的分钟数进行偏移。第三种方法不使用均时差；取而代之的是，使用恒星观测来给出恒星时，利用恒星时和平太阳时之间的关系。

1665年，克里斯蒂安·惠更斯发表了第一个以基本正确的管道给出均时差的表。惠更斯遵循托勒密和中世纪天文学家的传统，为均时差设定了它的值，使全年所有值都为正值。这意味着，与今天的平均时间相比，惠更斯的表中设定为平均时间的任何时钟，始终都慢了大约15分钟。

1672年至1673年，约翰·佛兰斯蒂德出版了另一套均时差表，他后来成为新的格林威治皇家天文台的第一位皇家天文学家。这些似乎是给出今天平均时间含义的第一个基本正确的表格（如上所述，之前均时差的符号总是正的，当日出的表观时间相对于日出的时钟时间最早时，它被设定为零）。佛兰斯蒂德采用了制表和命名校正的惯例，从某种意义上说，它将应用于表观时间以给出平均时间。。

均时差正确地基于太阳表观运动不规则性的两个主要组成部分，直到佛兰斯蒂德1672年至1673年的《表》与杰里迈亚·霍罗克斯的遗作一起出版后，才被普遍采用。

罗伯特·胡克（1635-1703）对万向接头进行了数学分析，他第一个注意到（非长期）均时差和万向接头的几何和数学描述是相同的，并提出在构建“机械日晷”时使用万向接头。

18世纪和19世纪初

佛兰斯蒂德1672-1673和1680年的表格中的修正基本上正确地计算了均时差，不需要进一步的偏移。但自那以后，由于三个因素，均时差表中的数值有所变化：

• 天文量测科技的改进带来了精度的普遍提高，
• 均时差缓慢的内在变化，是地球倾角和离心率长期变化的结果（例如，影响近日点的距离和日期），以及
• 太阳视运动中包含了17世纪未知但从18世纪开始发现的额外变化的小来源，包括月球（见质心）、金星和木星的影响。

1812年由赫斯特父子，用圆形刻度表示均时差的修正。这件作品现在正在德比博物馆与艺术画廊展出。

从1767年到1833年，英国的《航海年鉴和天文星历》将均时差制成表格，其含义是“在表观时间上加上或减去分钟数和秒数，以获得平均时间”。因为船上的时间通常是通过观测太阳来确定的，因此年鉴中的时间是视太阳时。在需要观测平均太阳时的异常情况下，才会执行此操作。在1834年以来的发行，所有时间都是平太阳时，因为从那时起，越来越多地船上的时间由航海钟来确定。因此，这些指示（按照指示）是将所述分钟数与平均时间相加或相减，以获得表观时间。所以现在加法对应于正均时差，减法对应于负均时差。

由于太阳的表观日运动是每天一圈，即每24小时360°，而太阳本身在天空中看起来是一个约0.5°的圆盘，因此最简单的日晷，可以读取到的时间最佳精度约为一分钟。由于均时差的范围约为33分钟，因此日晷时间和时钟时间之间的差异异不容忽视。除了均时差外，还必须根据与当地时区子午线的距离和夏令时（如果有的话）进行校正。

由于地球自转速度减慢，平均太阳日每世纪每天增加约2ms，目前每年累积约1秒。因为它在日晷的精度水准上是不可察觉的，因此这一微小的增加在均时差的传统定义中没有考虑在内。

主要部件

地球轨道的离心率

均时差（红色实线）及其两个分别绘制的主要分量，一部分是由于黄道的倾角（淡紫色虚线），另一部分是由于太阳沿黄道的视速度变化，这是由于地球轨道的离心率（深蓝色虚线和点线）。

地球绕着太阳转。从地球上看，太阳似乎在一年内通过背景恒星绕地球旋转一周。如果地球以恒定的速度绕太阳运行，在垂直于地轴的平面上以圆形轨道运行，那么太阳每天都会在同一时间中天，并且是一个完美的计时器（除了地球自转减慢的非常小的影响）。但地球的轨道是一个不以太阳为中心的椭圆，根据开普勒行星运动定律，它的速度在30.287到29.291公里/秒之间变化，它的角速度也在变化，因此太阳在近日点（目前约为1月3日）呈现移动得更快（相对于背景恒星），半年后在远日点的速度较慢。

在这些极端点，这种效应使视太阳日与平均值相差7.9秒/天。因此，在这些点之前，其它日子的较小每日速度差异是累积的，反映了地球与平均值相比是如何加速和减速的。

因此，地球轨道的离心率产生了一个周期性变化，在一阶近似下，该变化为正弦波，其中：

• 振幅：7.66 分钟
• 周期：1年
• 零点：近日点（1月初）和远日点（7月初）
• 极值：4月初（负值）和10月初（正值）

均时差的这一组成部分由上述因素“a”表示：

$a=-7.659\sin(6.240\,040\,77+0.017\,201\,97(365(y-2000)+d))$

黄赤交角

当地正午的太阳和行星（黄道带为红色，太阳和水星为黄色，金星为白色，火星为红色，木星为黄色与红色斑点，土星为白色与光环）。

即使地球的轨道是圆形的，人们感知到的太阳沿着我们的天球赤道的运动仍然是不均匀的。这是地球自转轴相对于轨道平面倾斜的结果；或者等效地，黄道（太阳在天球中的视路径）相对于天球赤道倾斜。这个运动投影在我们的天球赤道上，沿着它量测“时钟时间”，在至点达到最大值，当太阳的年运动平行于赤道（导致感知速度的放大），并且变化主要产生在赤经的值。这是分点时的最小值，此时太阳的视运动更倾斜，赤纬的变化最大，而赤经的变量最少，这是影响太阳日持续时间的唯一分量。倾角的一个实际例子是，即使在赤道上，太阳在日晷上投射的阴影在至点附近的每日偏移较小，在昼夜平分点附近的偏移较大。如果这种效应单独起作用，那么在至点附近的一天将长达24小时20.3秒（量测太阳中午到下一次太阳中午），在昼夜平分点附近比24小时短20.3秒。

在右图中，我们可以看到从地球上看到的太阳正午时分黄道平面视斜率的月度变化。这种变化是由于在太阳正午从太阳上看到的地球全年旋转的视进动造成的。

根据均时差，黄道的倾斜导致正弦波变化的贡献，包括：

• 振幅：9.87分钟
• 周期：1/2年
• 零点：分点和至点
• 极值：2月初和8月初（负）和5月初和11月初（正）

均时差的这一部分由上述系数“b”表示：

$b=9.863\sin \left(2(6.240\,040\,77+0.017\,201\,97(365(y-2000)+d))+3.5932\right)$

长期效应

上述两个因素具有不同的波长、振幅和相位，因此它们的组合贡献出一个不规则的波。在2000年历元，这些值（以分钟和秒为单位，使用UT日期）：

点	值	日期
最小值	−14 min 15 s	2月11日
0	0 min 00 s	4月15日
最大值	+3 min 41 s	5月14日
0	0 min 00 s	6月13日
最小值	−6 min 30 s	7月26日
0	0 min 00 s	9月1日
最大值	+16 min 25 s	11月3日
0	0 min 00 s	12月25日

均时差（E.T.）= 视太阳时 – 平太阳时。正值：太阳移动得比较快并且较早过中天，或是日晷的时间早于平太阳时。每年都会有微量的变化，但每四年一闰会重置这种变化。由于离心率和黄赤交角的长期变化，均时差曲线的确切形状和相关的日行迹在几个世纪中缓慢变化。在目前的时段，这两个值都在缓慢减少中，但是在实际上它们增减的变化是以数十万年的时间尺度上增加和减少。当离心率由目前的0.0167变化达到0.047时，离心率的效应会使轨道倾角的影响变得无足轻重，使得均时差的曲线上每年只有一个极大值与极小值。

在较短的时间尺度上（数千年），春分点和近日点日期的变化将更为重要。前者是由岁差引起的，与恒星相比，春分点向后移动。但在当前的讨论中，可以忽略不计，因为我们的公历的构造方式是将春分日期保持在3月20日（至少对于我们在这里的目标来说足够准确）。近日点的位移是向前的，大约为每个世纪1.7日。1246年，近日点的日期发生在12月22日，即冬至日，所以两者的波具有共同的零点，因此均时差曲线是对称的：在“天文算法”中，梅乌斯（英语：Meeus）给出了2月和11月的极值为15分39秒，而5月和7月的是4分58秒。在此之前，2月的最小值大于11月的最大值，5月的最大值大于7月的极小值。事实上，在公元前1900年（1901BCE）5月最大值大于11月最大值。在公元前2000年（2001BCE）5月的最大值 +12分20秒，而11月的最高值略低于10分钟。当人们将均时差的当前图表（见下文）与公元前2000年由托勒密的数据构建的的图表进行比较时，这种长期变化是显而易见的。

应用

如果日规（投射阴影的物体）上的晷针不是边缘的线段而是一个点（例如，板上的一个洞），则阴影（或光点）将在一天的过程中描绘出一条曲线。如果阴影投射在平面上，则此曲线将是一个圆锥截面（通常是双曲线），因为太阳运动的圆与圆柱上的点一起定义了一个圆锥体。在春分和秋分时，圆锥体退化为平面，双曲线退化为一条线。对于每天不同的双曲线，可以在每个双曲线上放置小时标记，其中包括任何必要的修正。

不幸的是，每个双曲线对应于两个不同的日子，每半年一个，这两天需要不同的修正。一个方便的折衷方案是画出“平均时间”的线，并添加一条曲线，显示一年中，正午阴影点的确切位置。这条曲线将类似数字8的形状，被称为日行迹。通过将日行迹与平均中午线进行比较，可以确定当天通常要应用的校正量。

均时差不仅用于日晷和类似设备，而且还用于太阳能的许多应用。像太阳跟踪器和定日镜这样的机器必须以受均时差影响的方式移动。

民用时是经常经过时区中心附近的子午线的当地平均时间，并且可能会因夏令时而进一步改变。当要找到对应于给定民用时的视太阳时，必须考虑关注地点与时区子午线之间的经度差、夏令时和均时差。

计算

均时差可以从已发布的表格或图表中获得。对于过去的日期，这些表格是根据历史量测或计算得出的；当然，对于未来的日期，只能计算得到表格。在电脑控制的定日镜等设备中，电脑通常使用程式设计来计算均时差。前者基于运动微分方程的数值积分，包括所有重要的引力和相对论效应。结果精确到1秒以上，是现代年鉴数据的基础。后者基于一种只包括太阳和地球之间引力相互作用的解决方案，比前者更简单，但不如前者准确。通过一些校正，包括少量的，可以提高其精度。

以下讨论描述了天文学家熟知的一种相当准确的均时差算法（在很长一段时间内与历书数据一致，误差在3秒内）。它还展示了如何获得一个简单的近似公式（在较长的时间间隔内精确到1分钟以内），该公式可以很容易地用计算器进行计算，并为本文前面使用的现象提供了简单的解释。

数学描述

均时差的精确定义是：

$\mathrm {EOT} =\mathrm {GHA} -\mathrm {GMHA}$

该方程式中出现的量为：

• EOT：均时差，即视太阳时和平太阳时之间的时间差；
• GHA：视太阳，及实际太阳的格林尼治时角；
• GMHA = 世界时（UT）- 偏移量，平太阳，即假设太阳的格林尼治平均时角。

这里的时间和角度是由以下因素相关的量： 2π 径度量 = 360° = 1&nbsp日 = 24 小时。因为GHA是一个可以量测的角度，而世界时UT是一个用于量测时间的尺规，因此EOT的差异是可量测的。偏移量 π = 180° = 12 需要从UT开始的小时数，因为UT在平均午夜为零，而 GMHA = 0 在平均中午。世界时在平均午夜是不连续的，所以为了形成连续的数量时间 t，另一个数量日数 N，一个整数，是必需的：t = N + UT/24小时天。与所有物理角度一样，GHA和GMHA在各自的（表观和平均）中午都有数学上的不连续性，但没有物理上的不间断性。尽管其组成部分在数学上存在不连续性，但EOT被定义为一个连续函数，通过在GHA和GMHA中不连续性之间的时间间隔内加（或减）24小时来实现

根据天球角度的定义GHA=GAST-'α'（见时角）
此处：

• GAST是格林尼治视恒星时（视春分点与赤道平面子午线之间的角度）。这是UT的一个已知功能。
• α是视太阳的赤经（视春分点和赤道平面上实际太阳之间的角度）。

当代入均时差时，它是：

$\mathrm {EOT} =\mathrm {GAST} -\alpha -\mathrm {UT} +\mathrm {offset}$

就像上面的GHA公式一样，可以写成

GMHA = GAST − α_M，

其中最后一项是平太阳的赤经。方程式通常用这些术语写成

$\mathrm {EOT} =\alpha _{M}-\alpha$

此处α_M = GAST − UT + offset。

在这个公式中，在特定时间值下EOT的量测或计算取决于当时的α。 α和α_M两者在一年中都是从0到24小时不等。前者在某个时间点具有不连续性，这取决于UT的值；而后者在稍晚的时间点具有其不连续性。因此，当以这种管道计算时，EOT有两个人为的不连续性。它们都可以通过从α中的不连续性之后和α_M中不连续性之前的小时间间隔内的EOT值中减去24小时来消除。由此产生的EOT是时间的连续函数。

另一个定义，表示为E，以区别于EOT，是

$E=\mathrm {GMST} -\alpha -\mathrm {UT} +\mathrm {offset}$

在这里GMST = GAST − eqeq，是格林尼治平恒星时间码（赤道平面上平春分点和平太阳之间的角度）。因此，GMST是GAST的近似值（和E是EOT的近似值）；由于摆动eqeq被称为昼夜平分点方程，或地球自转轴围绕其岁差运动的章动。由于章动运动的振幅仅为约1.2角秒（经度18角秒），因此EOT和E之间的差异可以忽略不计，除非对次秒级精度感兴趣。

第三个定义，表示为Δt以区别EOT和E，现在被称为星历时差（英语：Equation of Ephemeris Time）（在现在对EOT进行区分之前，E和Δt，后者被称为均时差）是

$\Delta t=\Lambda -\alpha$

这里Λ是平太阳的黄经度（在黄道平面上从平春分点到平太阳的角度）。

从1960年到2040年，Λ − (GMST − UT + offset)的区别是1.3秒。因此，在这个有限的年份范围内，Δ't'是EOT的近似值，其误差在0.1到2.5秒之间，具体取决于春分差中的经度校正；对于许多目的，例如校正日晷，这种精度已经绰绰有余。

赤经计算

赤经，以及均时差，可以从牛顿的天体运动二体理论中计算出来，在该理论中，描述了天体（地球和太阳）围绕其共同质心的椭圆轨道。根据这一理论，均时差变为：

$\Delta t=M+\lambda _{p}-\alpha$

其中出现的新角度是：

• M = 2π(t − t_p)/t_Y：平近点角，是从椭圆轨道的近心点到平太阳的角度；它的范围是从0到2π 当t从t_p增加至t_p + t_Y；
• t_Y = 7002365259635800000♠365.2596358天是近点年的时间长度：连续两次通过近日点的时间间隔；
• λ_p = Λ − M：近心点的黄道经度；
• t是动态时间，理论中的自变数。

在这里，认为它与基于UT的连续时间相同（见上文），但在更精确的计算（E或EOT）中，必须考虑它们之间的微小差异以及UT1和UTC之间的区别。

• t_p是t在近心点的值。

要完成计算，需要三个额外的角度：

• E：太阳的离心近点角（请注意，这与M的差异）；
• ν：太阳的真近点角；
• λ = ν + λ_p：太阳在黄道上的真实经度。

地心观察者看到的天球和太阳的椭圆轨道，看起来垂直于黄道，显示计算军时差所必需的6个角度（M, λ_p, α, ν, λ, E）。为清楚起见，图不按比例缩放。

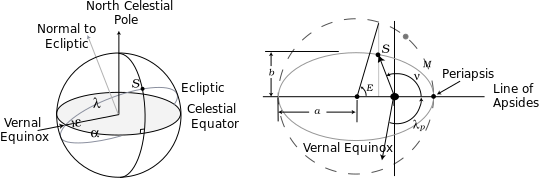
所有这些角度都显示在右图中，该图显示了从地球上看到的天球和太阳的椭圆轨道（与从太阳看到的地球轨道相同）。在此图中ε是倾角，而e = √1 − (b/a)²是椭圆的扁率。

现在给定的值为0 ≤ M ≤ 2π，通过以下众所周知的程式可以计算α(M)：

首先，鉴于M，从开普勒方程式计算E：

$M=E-e\sin {E}$

虽然这个方程式不能以封闭形式精确求解，E(M)的值可以从无穷级数（幂或三角）、图形或数值方法中获得。或者，请注意，对于e = 0, E = M，并通过反复运算：

$E\approx M+e\sin {M}$

这种近似值可以改进，对于小e，通过再次反复运算：

$E\approx M+e\sin {M}+{\frac {1}{2}}e^{2}\sin {2M}$,

并且继续反复运算会在e中连续产生幂级数展开的高阶项。对于较小的e（远小于 1）序列中的两个或三个项给出了E的良好近似值；e越小，则近似值越好。

接下来，了解E，从椭圆轨道关系计算真近点角ν

$\nu =2\arctan \left({\sqrt {\frac {1+e}{1-e}}}\tan {\tfrac {1}{2}}E\right)$

要使用的多值函数arctan x的正确分支生成ν，是从ν_E=0 = 0开始的连续函数{{math|E(M)}。因此，对于0 ≤ E < π，请使用arctan x = arctan x，对于π < E ≤ 2π，请使用arctan x = arctan x + π。对于特定值 E = π，其中tan的参数为无限，请使用ν = E。这里arctan x是主分支，{{math|1=|arctan x| < {{sfrac|π|2；计算机和电脑应用程序返回的函数。或者，此函数可以用其泰勒级数以e中表示，其前三项为：

$\nu \approx E+e\sin {E}+{\frac {1}{4}}e^{2}\sin {2E}$.

对于小e，这个近似值（甚至只是前两个项）是一个很好的近似值。 结合的近似值E(M)替换为ν(E)产生：

$\nu \approx M+2e\sin {M}+{\frac {5}{4}}e^{2}\sin {2M}$.

关系ν(M)称为中心差；这里的运算式是e中的二阶近似。对于小的e表征地球轨道的值，为ν(M)提供了一个非常好的近似值。

接下来，了解 ν，从它的定义计算λ：

$\lambda =\nu +\lambda _{p}$

由于轨道是椭圆而非圆，λ对应于 varies non-linearly with M的变化是非线性的。根据ν的近似值：

$\lambda \approx M+\lambda _{p}+2e\sin {M}+{\frac {5}{4}}e^{2}\sin {2M}$.

最后，知道λ，从上面所示的天球上直角三角形的关系计算 α

$\alpha =\arctan \left(\cos {\varepsilon }\tan {\lambda }\right)$

请注意，α的象限与λ相同，因此将λ减小到0到2 π的范围，并写为

$\alpha =\arctan \left(\cos {\varepsilon }\tan {\lambda }+k\pi \right)$,

此处如果λ位于象限1中，k是0。如果λ在象限2或3，k是1；如果λ在象限4，k是2。对于 tan为无限的值，α = λ。

虽然α的近似值可以从截断的泰勒级数中获得，就像{{math|ν一样，使用以下方程更有效

$\alpha =\lambda -\arcsin \left(y\sin \left(\alpha +\lambda \right)\right)$

此处y = tan²(ε/2)。 请注意，对于ε = y = 0，α = λ并反复运算两次：

$\alpha \approx \lambda -y\sin {2\lambda }+{\frac {1}{2}}y^{2}\sin {4\lambda }$。

相关条目

• 平太阳
• 真太阳

参考资料

• J. Meeus, Mathematical astronomy morsels, ISBN 0-943396-51-4

外部链接

• DestinyNet 命理网 真太阳时/均时差计算程式 （页面存档备份，存于互联网档案馆）
• Novel Visualisation of Equation of Time - Constantly updated
• Table giving the Equation of Time and the declination of the sun for every day of the year
• Sundials on the Internet （页面存档备份，存于互联网档案馆）
• The equation of time described on the Royal Greenwich Observatory website
• An analemma site with many illustrations （页面存档备份，存于互联网档案馆）
• The Equation of Time and the Analemma, by Kieron Taylor
• An article by Brian Tung containing a link to a C program using a more accurate formula than most (particularly at high inclinations and eccentricities). The program can calculate solar declination, Equation of Time, or Analemma.
• Doing calculations using Ptolemy's ephemeres, such as his E.T. graph （页面存档备份，存于互联网档案馆）
• A dynamic and unique Equation of Time visualisation.
• Equation of Time function for Excel, CAD or other programs. The Sun API is free and extremely accurate. For Windows computers.
• The equation of time correction-table （页面存档备份，存于互联网档案馆） A page describing how to correct a clock to a sundial.
• An example （页面存档备份，存于互联网档案馆） of an Audemars Piguet mechanical wristwatch containing this concept as a complication, including a description of the implementation in horology and several videos/animations.
• Two more examples of a mechanical wristwatch containing this complication, manufactured by Blancpain: Part 1 Part 2.