广义相对论中的开普勒问题 ,是指在广义相对论 的框架下求解存在引力相互作用 的两体动力学问题 。在典型情况下以及本文中,其中一个物体的质量
m
{\displaystyle m}
M
{\displaystyle M}
地球 绕太阳 公转,以及一个光子 在一颗恒星 的引力场 中的运动等问题。在这些情形下,可以认为大质量
M
{\displaystyle M}
爱因斯坦场方程 的史瓦西解 来描述;而小质量
m
{\displaystyle m}
测地线方程 来描述。由于假设小质量
m
{\displaystyle m}
潮汐力 可忽略。
从测地线方程可以推出广义相对论的关键性实验证据 ,著名的水星 近日点 的进动 ,以及光线在太阳引力场中的偏折。对于前者,广义相对论为观测到的这一现象提供了漂亮的解释,而后者则是广义相对论的著名预言,其正确性被亚瑟·爱丁顿 爵士的实验观测所证实。
广义相对论的两体问题中还涉及了引力辐射造成的轨道衰减,这是一个纯粹的相对论效应,没有对应的经典力学版本。这个问题并不包含在史瓦西解中,请参见引力辐射 和引力波天文学 。
没有其他外力存在时,一个粒子在牛顿有心力 的作用下绕着另一个粒子公转的轨道永远是一个不变的椭圆稳定轨道。当有其他外力存在(例如来自其他行星的引力)时,这样的轨道会逐渐发生转动,这种转动(被称作轨道进动)的速率可以被测量得非常精确。如果知道了这些外力的大小和方向,通过牛顿力学也可以对这种轨道进动的速率进行理论预测。不过在1859年对水星轨道进动的观测中,牛顿力学没有给出和实验观察相一致的预言。 1859年,法国天文学家于尔班·勒威耶 发现水星的实际轨道进动与预期的并不十分相符:即使考虑到太阳系中其他行星 的影响,实际的进动速度还是要比牛顿 的经典理论稍微快一点。[ 1] 祝融星 ”等。[ 2] :253-256 在这些解释被一一否决后,有些物理学家提出了更激进的猜想,认为牛顿的引力平方反比律 并不严格成立。例如某些人提出定律中的指数并不严格为2,而某些人如亨德里克·洛伦兹 提出牛顿的万有引力定律应增加与速度有关的引力势修正项。[ 2] :254
1905年,爱因斯坦提出了狭义相对论 ,这一理论否决了任何超过光速传播的效应的可能性;不过同时,这也暗示了相对论的基本假设和牛顿天体力学的矛盾。拉普拉斯 早先在其研究中证明,如果引力相互作用不是超距的(即传播是瞬时的),行星的运动将不再严格满足动量守恒定律 (类似于电磁相互作用 中一部分动量 要传递给电磁相互作用的媒介子 ,引力相互作用中也需要携带动量的媒介子)。从牛顿力学的观点来看,如果引力相互作用只能以有限速度传播,那么在任意时刻,行星受到的来自太阳的引力将不会指向太阳所在的即时位置,而是在若干时间之前的位置。在经典力学的基础上,拉普拉斯推导出当引力以光速传播时太阳系是不稳定的,并只能维持并不太长时间的存在。而对太阳系的实际观测表明,如果引力的传播速度确实存在一个上限,根据经典力学这个上限将比光速高出好几个数量级。[ 3] :177
这种矛盾引出了建立一个替代牛顿引力理论的新理论的需求,这个新理论需要满足狭义相对论的基本假设,并且在相对论效应可忽略时能够和牛顿的引力理论相容。1907年爱因斯坦确认了建立一个狭义相对论的后继理论的必要性,这个理论能够同时包含狭义相对论的基本假设和万有引力相互作用。[ 4] 等效原理 的基础上逐渐发展了他的新理论。根据等效原理,一个均匀引力场对在其内所有物体的作用都是相同的,因此这个引力场将不能被一个处于自由落体 状态的观察者观测到。归纳而言,所有局部的引力效应都可以在一个直线加速的非惯性参考系 中体现出来,这个原理反过来也成立,即加速参考系等效于一个局部的引力场。这样看来,引力和离心力 以及科里奥利力 等惯性力 这样的“虚拟力 ”有相类似的效应:惯性力都来源于一个加速的非惯性系,并且和物体的惯性质量 成正比,引力亦然(由于惯性质量和引力质量 等价)。想要在等效原理的基础上将万有引力和狭义相对论的基本假设统一起来,需要牺牲的是经典力学中习以为常的基本假设:我们所处的时空是一个符合欧几里得几何 的平直时空。爱因斯坦使用的是一种更广义的几何学:黎曼几何 ,在黎曼几何描述下的时空可以是弯曲的。经过八年的研究,他成功得到了一个能够包含引力理论的更具功能的相对论性理论:广义相对论。广义相对论要求时空是弯曲的,这种时空的弯曲性是引力的体现,也是一种物理上的实在,这和惯性力不过是假想的“虚力”完全不同。广义相对论首先成功解释了水星 近日点 的进动 误差并预言了光线在太阳引力场中的偏折,这个预言在广义相对论发表之后得到了实验证实。[ 2] :ch. 9-15 [ 5] [ 6] :110ff
在经典的欧几里得几何中,三角形满足勾股定理 (毕达哥拉斯定理),这意味着空间中两点间的距离平方等于空间中所有完备正交分量平方和:
d
s
2
=
d
x
2
+
d
y
2
+
d
z
2
{\displaystyle ds^{2}=dx^{2}+dy^{2}+dz^{2}}
这里
d
x
{\displaystyle dx}
d
y
{\displaystyle dy}
d
z
{\displaystyle dz}
笛卡尔坐标系 下三个坐标轴
x
{\displaystyle x}
y
{\displaystyle y}
z
{\displaystyle z}
现在想象存在一个笛卡尔坐标不适用的世界,其间两点的距离由下式描述:
d
s
2
=
F
(
x
,
y
,
z
)
d
x
2
+
G
(
x
,
y
,
z
)
d
y
2
+
H
(
x
,
y
,
z
)
d
z
2
{\displaystyle ds^{2}=F(x,y,z)dx^{2}+G(x,y,z)dy^{2}+H(x,y,z)dz^{2}}
这里
F
{\displaystyle F}
G
{\displaystyle G}
H
{\displaystyle H}
x
{\displaystyle x}
y
{\displaystyle y}
z
{\displaystyle z}
球坐标系
(
r
,
θ
,
ϕ
)
{\displaystyle (r,\theta ,\phi )}
d
s
2
=
d
r
2
+
r
2
d
θ
2
+
r
2
sin
2
θ
d
ϕ
2
{\displaystyle ds^{2}=dr^{2}+r^{2}d\theta ^{2}+r^{2}\sin ^{2}\theta d\phi ^{2}}
进一步的想象可能会比较困难,但我们假设存在一个用来测量长度的尺子不再可靠的世界:尺子的长度会因其位置甚至摆放方向而改变。这是最一般的情况,在计算两点间距离时需要考虑交叉项的存在:
d
s
2
=
g
x
x
d
x
2
+
g
x
y
d
x
d
y
+
g
x
z
d
x
d
z
+
⋯
+
g
z
y
d
z
d
y
+
g
z
z
d
z
2
{\displaystyle ds^{2}=g_{xx}dx^{2}+g_{xy}dxdy+g_{xz}dxdz+\cdots +g_{zy}dzdy+g_{zz}dz^{2}}
这里九个函数
g
x
y
{\displaystyle g_{xy}}
度规 张量 ,它定义了黎曼几何框架下的空间几何。在球坐标系下交叉项不存在,它只包含有三个非零的张量元素。[ 7] :65-69
在狭义相对论中,爱因斯坦就已经指出空间中两点的距离并不是恒量,而与观察者的运动(即惯性参考系)有关。狭义相对论指出在任何惯性系 下观测到的恒量是两点间的时空间隔,这个间隔被称作固有时 。固有时是一个相对论不变量,它与惯性参考系无关。[ 8] :ch. 2:19-18
c
2
d
τ
2
=
c
2
d
t
2
−
d
x
2
−
d
y
2
−
d
z
2
{\displaystyle c^{2}d\tau ^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}}
在球坐标下这可以写成
c
2
d
τ
2
=
c
2
d
t
2
−
d
r
2
−
r
2
d
θ
2
−
r
2
sin
2
θ
d
ϕ
2
{\displaystyle c^{2}d\tau ^{2}=c^{2}dt^{2}-dr^{2}-r^{2}d\theta ^{2}-r^{2}\sin ^{2}\theta d\phi ^{2}}
这些公式都可以看作是毕达哥拉斯定理的自然推广,它们仅在时空曲率为零时成立。但在广义相对论的框架下,时间和空间都可以是弯曲的,这时的时空间隔需要写成更一般的形式:
c
2
d
τ
2
=
g
μ
ν
d
x
μ
d
x
ν
{\displaystyle c^{2}d\tau ^{2}=g_{\mu \nu }dx^{\mu }dx^{\nu }}
这里的度规
g
{\displaystyle g}
爱因斯坦的引力场方程 。爱因斯坦的引力理论不仅和当时已知的物理定律相容,它还成功预言了很多从未观测到的物理现象,这些现象至今仍然不断被实验观测所证实。
爱因斯坦场方程的解的最简单形式是史瓦西度规 ,它对应着一个不带电荷 和角动量 的球对称的质量
M
{\displaystyle M}
[ 8] :ch 2:19
c
2
d
τ
2
=
(
1
−
r
s
r
)
c
2
d
t
2
−
d
r
2
1
−
r
s
r
−
r
2
d
θ
2
−
r
2
sin
2
θ
d
φ
2
{\displaystyle c^{2}{d\tau }^{2}=\left(1-{\frac {r_{s}}{r}}\right)c^{2}dt^{2}-{\frac {dr^{2}}{1-{\frac {r_{s}}{r}}}}-r^{2}d\theta ^{2}-r^{2}\sin ^{2}\theta d\varphi ^{2}}
其中,
τ
{\displaystyle \tau }
c
{\displaystyle c}
t
{\displaystyle t}
r
{\displaystyle r}
θ
{\displaystyle \theta }
ϕ
{\displaystyle \phi }
r
s
{\displaystyle r_{s}}
M
{\displaystyle M}
史瓦西半径 ,其关系为
r
s
=
2
G
M
c
2
{\displaystyle r_{s}={\frac {2GM}{c^{2}}}}
牛顿经典力学下引力的传播速度无限大,与光速无关:这可以看作是在经典近似下史瓦西半径趋于零,这时的史瓦西度规还原为狭义相对论的形式。在一般情形下,史瓦西半径总是非常小的,例如地球的史瓦西半径只有9毫米,[ 8] :ch 2:39 而一颗人造卫星 的同步轨道 半径是它的四十亿倍,为42164千米。即使是在地球表面,广义相对论对牛顿引力的修正也只有十亿分之一。然而在宇宙中的致密星体如黑洞 和中子星 的周围,广义相对论的效应就变得非常明显。
根据广义相对论,质量可忽略的粒子在引力场中沿着测地线 运动。在无引力的平直时空中,测地线是直线;但当时空存在弯曲时,测地线由下面的测地线方程 描述:[ 9] :185-201 [ 10] :156-157
d
2
x
μ
d
q
2
+
Γ
ν
λ
μ
d
x
ν
d
q
d
x
λ
d
q
=
0
{\displaystyle {\frac {d^{2}x^{\mu }}{dq^{2}}}+\Gamma _{\nu \lambda }^{\mu }{\frac {dx^{\nu }}{dq}}{\frac {dx^{\lambda }}{dq}}=0}
这里
Γ
{\displaystyle \Gamma }
克里斯托费尔符号 而变量
q
{\displaystyle q}
世界线 )参数化的参量。克里斯托费尔符号只和度规对于坐标的一阶偏导数 有关(即描述了度规如何随坐标变化)。[ 注 1] 类时 轨迹(速度小于光速的带质量粒子的运动轨迹)而言,参数
q
{\displaystyle q}
类光 轨迹(呈光速的零质量粒子的运动轨迹),固有时为零,因此严格来讲不能将固有时用作参数;不过类光可以看作是类时的极端相对论案例,有时从而可以通过取极限的方法,从类时的轨迹导出粒子质量为零时类光的轨迹,并保持总能量不变。
在度规具有对称性 的场合下我们往往可以将问题简化。例如史瓦西度规是关于平面
θ
=
π
/
2
{\displaystyle \theta =\pi /2}
θ
{\displaystyle \theta }
π
/
2
{\displaystyle \pi /2}
c
2
d
τ
2
=
(
1
−
r
s
r
)
c
2
d
t
2
−
d
r
2
1
−
r
s
r
−
r
2
d
φ
2
.
{\displaystyle c^{2}d\tau ^{2}=\left(1-{\frac {r_{s}}{r}}\right)c^{2}dt^{2}-{\frac {dr^{2}}{1-{\frac {r_{s}}{r}}}}-r^{2}d\varphi ^{2}.}
从这个形式可得到两个运动的守恒量,单位质量的角动量和单位质量的能量(参见下文注释)[ 8] :ch 3:9, ch 4:4
r
2
d
φ
d
τ
=
L
m
,
{\displaystyle r^{2}{\frac {d\varphi }{d\tau }}={\frac {L}{m}},}
(
1
−
r
s
r
)
d
t
d
τ
=
E
m
c
2
.
{\displaystyle \left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}={\frac {E}{mc^{2}}}.}
将这两个守恒量代入史瓦西度规中得到粒子的运动方程
(
d
r
d
τ
)
2
=
E
2
m
2
c
2
−
(
1
−
r
s
r
)
(
c
2
+
L
2
m
2
r
2
)
.
{\displaystyle \left({\frac {dr}{d\tau }}\right)^{2}={\frac {E^{2}}{m^{2}c^{2}}}-\left(1-{\frac {r_{s}}{r}}\right)\left(c^{2}+{\frac {L^{2}}{m^{2}r^{2}}}\right).}
通过角动量
L
{\displaystyle L}
(
d
r
d
φ
)
2
=
(
d
r
d
τ
)
2
(
d
τ
d
φ
)
2
=
(
d
r
d
τ
)
2
(
m
r
2
L
)
2
,
{\displaystyle \left({\frac {dr}{d\varphi }}\right)^{2}=\left({\frac {dr}{d\tau }}\right)^{2}\left({\frac {d\tau }{d\varphi }}\right)^{2}=\left({\frac {dr}{d\tau }}\right)^{2}\left({\frac {mr^{2}}{L}}\right)^{2},}
这样就得到了粒子的轨道方程
(
d
r
d
φ
)
2
=
r
4
b
2
−
(
1
−
r
s
r
)
(
r
4
a
2
+
r
2
)
{\displaystyle \left({\frac {dr}{d\varphi }}\right)^{2}={\frac {r^{4}}{b^{2}}}-\left(1-{\frac {r_{s}}{r}}\right)\left({\frac {r^{4}}{a^{2}}}+r^{2}\right)}
其中的两个长度参数
a
{\displaystyle a}
b
{\displaystyle b}
a
=
L
m
c
,
{\displaystyle a={\frac {L}{mc}},}
b
=
c
L
E
.
{\displaystyle b={\frac {cL}{E}}.}
利用最小作用量原理 [ 11] :389-393 或哈密顿-雅可比方程 [ 12] :299-309 可得到相同形式的轨道方程(见后文),轨道方程的解为
φ
=
∫
d
r
r
2
1
b
2
−
(
1
−
r
s
r
)
(
1
a
2
+
1
r
2
)
.
{\displaystyle \varphi =\int {\frac {dr}{r^{2}{\sqrt {{\frac {1}{b^{2}}}-\left(1-{\frac {r_{s}}{r}}\right)\left({\frac {1}{a^{2}}}+{\frac {1}{r^{2}}}\right)}}}}.}
1919年亚瑟·爱丁顿 爵士所测量的星光在太阳引力场中的偏折实验使得广义相对论在全世界范围内被广为接受 对于上面的史瓦西度规中的粒子轨道方程,当粒子质量趋于零(或长度参数
a
{\displaystyle a}
φ
=
∫
d
r
r
2
1
b
2
−
(
1
−
r
s
r
)
1
r
2
{\displaystyle \varphi =\int {\frac {dr}{r^{2}{\sqrt {{\frac {1}{b^{2}}}-\left(1-{\frac {r_{s}}{r}}\right){\frac {1}{r^{2}}}}}}}}
将此式按
r
s
/
r
{\displaystyle r_{s}/r}
[ 10] :293-294
δ
φ
≈
2
r
s
b
=
4
G
M
c
2
b
.
{\displaystyle \delta \varphi \approx {\frac {2r_{s}}{b}}={\frac {4GM}{c^{2}b}}.}
这里长度参数
b
{\displaystyle b}
引力透镜 的测量中它都相当精确,这是因为对大多数星体而言
r
s
/
r
{\displaystyle r_{s}/r}
[ 13]
从上面得到的史瓦西度规中的粒子运动方程
(
d
r
d
τ
)
2
=
E
2
m
2
c
2
−
c
2
+
r
s
c
2
r
−
L
2
m
2
r
2
+
r
s
L
2
m
2
r
3
{\displaystyle \left({\frac {dr}{d\tau }}\right)^{2}={\frac {E^{2}}{m^{2}c^{2}}}-c^{2}+{\frac {r_{s}c^{2}}{r}}-{\frac {L^{2}}{m^{2}r^{2}}}+{\frac {r_{s}L^{2}}{m^{2}r^{3}}}}
可通过代入史瓦西半径的定义得到
1
2
m
(
d
r
d
τ
)
2
=
[
E
2
2
m
c
2
−
1
2
m
c
2
]
+
G
M
m
r
−
L
2
2
m
r
2
+
G
M
L
2
c
2
m
r
3
{\displaystyle {\frac {1}{2}}m\left({\frac {dr}{d\tau }}\right)^{2}=\left[{\frac {E^{2}}{2mc^{2}}}-{\frac {1}{2}}mc^{2}\right]+{\frac {GMm}{r}}-{\frac {L^{2}}{2mr^{2}}}+{\frac {GML^{2}}{c^{2}mr^{3}}}}
这个运动方程相当于一个质量为
m
{\displaystyle m}
势阱 中运动,其有效势能为[ 10] :284
V
(
r
)
=
−
G
M
m
r
+
L
2
2
m
r
2
−
G
M
L
2
c
2
m
r
3
{\displaystyle V(r)=-{\frac {GMm}{r}}+{\frac {L^{2}}{2mr^{2}}}-{\frac {GML^{2}}{c^{2}mr^{3}}}}
式中前两项是经典力学的结果:第一项是牛顿引力势能 (负值表示吸引),第二项是具有排斥效应的离心势能;而第三项仅在广义相对论中存在,它代表的是一个与距离立方成反比的吸引势能。从后文或其他文献中可以看到,这种立方反比势能造成了粒子运动周期中椭圆轨道的逐渐相对论进动,每个周期内进动的角位移为[ 14] :157
δ
φ
≈
6
π
G
M
c
2
A
(
1
−
e
2
)
{\displaystyle \delta \varphi \approx {\frac {6\pi GM}{c^{2}A\left(1-e^{2}\right)}}}
其中
A
{\displaystyle A}
e
{\displaystyle e}
在
r
{\displaystyle r}
r
i
n
n
e
r
{\displaystyle r_{\mathrm {inner} }}
a
=
L
/
m
c
{\displaystyle a=L/mc}
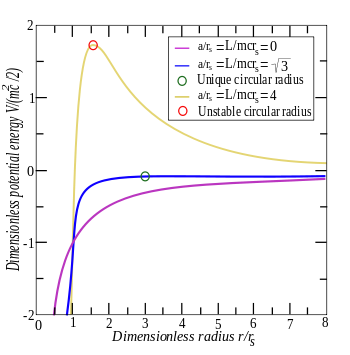
不同角动量对应的有效径向势能。半径很小时,势能迅速下降,这使得粒子向
r
=
0
{\displaystyle r=0}
a
/
r
s
=
L
/
m
c
r
s
{\displaystyle a/r_{s}=L/mcr_{s}}
3
{\displaystyle {\sqrt {3}}}
如果使用长度参数
a
{\displaystyle a}
V
{\displaystyle V}
V
(
r
)
=
m
c
2
2
[
−
r
s
r
+
a
2
r
2
−
r
s
a
2
r
3
]
{\displaystyle V(r)={\frac {mc^{2}}{2}}\left[-{\frac {r_{s}}{r}}+{\frac {a^{2}}{r^{2}}}-{\frac {r_{s}a^{2}}{r^{3}}}\right]}
当有效力为零时,得到粒子的圆轨道:
F
=
−
d
V
d
r
=
−
m
c
2
2
r
4
[
r
s
r
2
−
2
a
2
r
+
3
r
s
a
2
]
=
0
{\displaystyle F=-{\frac {dV}{dr}}=-{\frac {mc^{2}}{2r^{4}}}\left[r_{s}r^{2}-2a^{2}r+3r_{s}a^{2}\right]=0}
有效力为零的含义即为吸引力(牛顿引力加广义相对论的立方反比引力)和排斥力(等效的离心力)恰巧平衡。在两个半径上可以满足这种平衡条件,它们被记为
r
o
u
t
e
r
{\displaystyle r_{\mathrm {outer} }}
r
i
n
n
e
r
{\displaystyle r_{\mathrm {inner} }}
[ 10] :286
r
o
u
t
e
r
=
a
2
r
s
(
1
+
1
−
3
r
s
2
a
2
)
{\displaystyle r_{\mathrm {outer} }={\frac {a^{2}}{r_{s}}}\left(1+{\sqrt {1-{\frac {3r_{s}^{2}}{a^{2}}}}}\right)}
r
i
n
n
e
r
=
a
2
r
s
(
1
−
1
−
3
r
s
2
a
2
)
=
3
a
2
r
o
u
t
e
r
{\displaystyle r_{\mathrm {inner} }={\frac {a^{2}}{r_{s}}}\left(1-{\sqrt {1-{\frac {3r_{s}^{2}}{a^{2}}}}}\right)={\frac {3a^{2}}{r_{\mathrm {outer} }}}}
其中靠内的半径
r
i
n
n
e
r
{\displaystyle r_{\mathrm {inner} }}
r
{\displaystyle r}
r
o
u
t
e
r
{\displaystyle r_{\mathrm {outer} }}
当长度参数
a
{\displaystyle a}
r
s
{\displaystyle r_{s}}
r
o
u
t
e
r
≈
2
a
2
r
s
{\displaystyle r_{\mathrm {outer} }\approx {\frac {2a^{2}}{r_{s}}}}
r
i
n
n
e
r
≈
3
2
r
s
{\displaystyle r_{\mathrm {inner} }\approx {\frac {3}{2}}r_{s}}
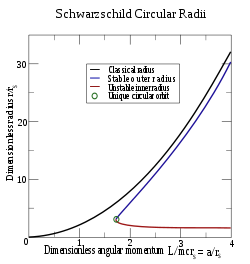
稳定轨道与不稳定轨道的半径关于归一化角动量
a
/
r
s
=
L
/
m
c
r
s
{\displaystyle a/r_{s}=L/mcr_{s}}
3
{\displaystyle {\sqrt {3}}}
直接在经典理论下让惯性离心力等于牛顿万有引力:
m
ω
φ
2
r
=
G
M
m
r
2
{\displaystyle m\omega _{\varphi }^{2}r={\frac {GMm}{r^{2}}}}
这里
ω
φ
{\displaystyle \omega _{\varphi }}
ω
φ
2
≈
G
M
r
o
u
t
e
r
3
=
(
r
s
c
2
2
r
o
u
t
e
r
3
)
=
(
r
s
c
2
2
)
(
r
s
3
8
a
6
)
=
c
2
r
s
4
16
a
6
{\displaystyle \omega _{\varphi }^{2}\approx {\frac {GM}{r_{\mathrm {outer} }^{3}}}=\left({\frac {r_{s}c^{2}}{2r_{\mathrm {outer} }^{3}}}\right)=\left({\frac {r_{s}c^{2}}{2}}\right)\left({\frac {r_{s}^{3}}{8a^{6}}}\right)={\frac {c^{2}r_{s}^{4}}{16a^{6}}}}
在另一种情形下,当
a
2
{\displaystyle a^{2}}
3
r
s
2
{\displaystyle 3r_{s}^{2}}
[ 10] :286
r
o
u
t
e
r
≈
r
i
n
n
e
r
≈
3
r
s
{\displaystyle r_{\mathrm {outer} }\approx r_{\mathrm {inner} }\approx 3r_{s}}
上面给出的
r
i
n
n
e
r
{\displaystyle r_{\mathrm {inner} }}
r
o
u
t
e
r
{\displaystyle r_{\mathrm {outer} }}
r
o
u
t
e
r
{\displaystyle r_{\mathrm {outer} }}
3
r
s
{\displaystyle 3r_{s}}
r
i
n
n
e
r
{\displaystyle r_{\mathrm {inner} }}
3
/
2
r
s
{\displaystyle 3/2r_{s}}
3
r
s
{\displaystyle 3r_{s}}
3
/
2
r
s
{\displaystyle 3/2r_{s}}
a
{\displaystyle a}
r
i
n
n
e
r
=
3
/
2
r
s
{\displaystyle r_{\mathrm {inner} }=3/2r_{s}}
光子球 ”(photon sphere)。
在非相对论开普勒问题 中,粒子永远沿着同样的椭圆轨道运动(红色轨道)。广义相对论引入了第三种力的作用,这种力对粒子的吸引比牛顿引力稍强,特别是在轨道半径很短的情形。这种力使行星的椭圆轨道产生进动(蓝色轨道),现在实验上已经测量了水星 、金星 和地球的相应进动。图中黄色的点表示轨道的中心质量,例如太阳。 从史瓦西几何中得到的径向有效势能
V
{\displaystyle V}
r
o
u
t
e
r
{\displaystyle r_{\mathrm {outer} }}
r
o
u
t
e
r
{\displaystyle r_{\mathrm {outer} }}
ω
r
2
=
1
m
[
d
2
V
d
r
2
]
r
=
r
o
u
t
e
r
{\displaystyle \omega _{r}^{2}={\frac {1}{m}}\left[{\frac {d^{2}V}{dr^{2}}}\right]_{r=r_{\mathrm {outer} }}}
用有效势能
V
{\displaystyle V}
ω
r
2
=
(
c
2
r
s
2
r
o
u
t
e
r
4
)
(
r
o
u
t
e
r
−
r
i
n
n
e
r
)
=
ω
φ
2
1
−
3
r
s
2
a
2
{\displaystyle \omega _{r}^{2}=\left({\frac {c^{2}r_{s}}{2r_{\mathrm {outer} }^{4}}}\right)\left(r_{\mathrm {outer} }-r_{\mathrm {inner} }\right)=\omega _{\varphi }^{2}{\sqrt {1-{\frac {3r_{s}^{2}}{a^{2}}}}}}
两边开平方并作二项式展开:
ω
r
=
ω
φ
(
1
−
3
r
s
2
4
a
2
+
⋯
)
{\displaystyle \omega _{r}=\omega _{\varphi }\left(1-{\frac {3r_{s}^{2}}{4a^{2}}}+\cdots \right)}
而后再乘以公转的周期
T
{\displaystyle T}
δ
φ
=
T
(
ω
φ
−
ω
r
ω
φ
)
≈
2
π
(
3
r
s
2
4
a
2
)
=
3
π
m
2
c
2
2
L
2
r
s
2
{\displaystyle \delta \varphi =T\left({\frac {\omega _{\varphi }-\omega _{r}}{\omega _{\varphi }}}\right)\approx 2\pi \left({\frac {3r_{s}^{2}}{4a^{2}}}\right)={\frac {3\pi m^{2}c^{2}}{2L^{2}}}r_{s}^{2}}
这里我们用到了
ω
T
=
2
π
{\displaystyle \omega T=2\pi }
a
{\displaystyle a}
r
s
{\displaystyle r_{s}}
[ 8] :C:9-10
δ
φ
≈
3
π
m
2
c
2
2
L
2
(
4
G
2
M
2
c
4
)
=
6
π
G
2
M
2
m
2
c
2
L
2
{\displaystyle \delta \varphi \approx {\frac {3\pi m^{2}c^{2}}{2L^{2}}}\left({\frac {4G^{2}M^{2}}{c^{4}}}\right)={\frac {6\pi G^{2}M^{2}m^{2}}{c^{2}L^{2}}}}
根据开普勒第三定律 ,使用椭圆的半长轴
A
{\displaystyle A}
e
{\displaystyle e}
[ 15] :95
L
2
G
M
m
2
=
A
(
1
−
e
2
)
{\displaystyle {\frac {L^{2}}{GMm^{2}}}=A\left(1-e^{2}\right)}
这样就得到了上面看到的进动角位移公式
δ
φ
≈
6
π
G
M
c
2
A
(
1
−
e
2
)
{\displaystyle \delta \varphi \approx {\frac {6\pi GM}{c^{2}A\left(1-e^{2}\right)}}}
轨道方程[ 16] :710-711
(
d
r
d
φ
)
2
=
r
4
b
2
−
(
1
−
r
s
r
)
(
r
4
a
2
+
r
2
)
{\displaystyle \left({\frac {dr}{d\varphi }}\right)^{2}={\frac {r^{4}}{b^{2}}}-\left(1-{\frac {r_{s}}{r}}\right)\left({\frac {r^{4}}{a^{2}}}+r^{2}\right)}
可以通过引入一个无量纲量来化简:
ζ
=
r
s
4
r
−
1
12
{\displaystyle \zeta ={\frac {r_{s}}{4r}}-{\frac {1}{12}}}
这时轨道方程可表示为
(
d
ζ
d
φ
)
2
=
4
ζ
3
−
g
2
ζ
−
g
3
,
{\displaystyle \left({\frac {d\zeta }{d\varphi }}\right)^{2}=4\zeta ^{3}-g_{2}\zeta -g_{3},}
这里的无量纲系数
g
2
{\displaystyle g_{2}}
g
3
{\displaystyle g_{3}}
g
2
=
1
12
−
r
s
2
4
a
2
,
g
3
=
1
216
+
r
s
2
24
a
2
−
r
s
2
16
b
2
.
{\displaystyle {\begin{aligned}g_{2}&={\frac {1}{12}}-{\frac {r_{s}^{2}}{4a^{2}}},\\g_{3}&={\frac {1}{216}}+{\frac {r_{s}^{2}}{24a^{2}}}-{\frac {r_{s}^{2}}{16b^{2}}}.\end{aligned}}}
这个微分方程的解为
φ
−
φ
0
=
∫
d
ζ
4
ζ
3
−
g
2
ζ
−
g
3
.
{\displaystyle \varphi -\varphi _{0}=\int {\frac {d\zeta }{\sqrt {4\zeta ^{3}-g_{2}\zeta -g_{3}}}}.}
其中无量纲量
ζ
=
℘
(
φ
−
φ
0
)
{\displaystyle \zeta =\wp (\varphi -\varphi _{0})}
℘
{\displaystyle \wp }
g
2
{\displaystyle g_{2}}
g
3
{\displaystyle g_{3}}
魏尔施特拉斯椭圆函数 ,
φ
0
{\displaystyle \varphi _{0}}
对于轨道方程[ 16] :713-714
(
d
ζ
d
φ
)
2
=
4
ζ
3
−
g
2
ζ
−
g
3
,
{\displaystyle \left({\frac {d\zeta }{d\varphi }}\right)^{2}=4\zeta ^{3}-g_{2}\zeta -g_{3},}
如果右边三次多项式的判别式
Δ
=
g
2
3
−
27
g
3
2
{\displaystyle \Delta =g_{2}^{3}-27g_{3}^{2}}
三次方程
G
(
ζ
)
=
4
ζ
3
−
g
2
ζ
−
g
3
=
0
{\displaystyle G(\zeta )=4\zeta ^{3}-g_{2}\zeta -g_{3}=0}
有三个实根,
e
1
{\displaystyle e_{1}}
e
2
{\displaystyle e_{2}}
e
3
{\displaystyle e_{3}}
e
1
>
e
2
>
e
3
.
{\displaystyle e_{1}>e_{2}>e_{3}.}
在此情形下,方程的解
ζ
=
℘
(
φ
−
φ
0
)
{\displaystyle \zeta =\wp (\varphi -\varphi _{0})}
椭圆函数 ,其中一个完全是实的:
ω
1
=
∫
e
1
∞
d
z
4
z
3
−
g
2
z
−
g
3
{\displaystyle \omega _{1}=\int _{e_{1}}^{\infty }{\frac {dz}{\sqrt {4z^{3}-g_{2}z-g_{3}}}}}
而另一个完全是虚的:
ω
3
=
i
∫
−
e
3
∞
d
z
4
z
3
−
g
2
z
−
g
3
{\displaystyle \omega _{3}=i\int _{-e_{3}}^{\infty }{\frac {dz}{\sqrt {4z^{3}-g_{2}z-g_{3}}}}}
剩下的那一个根对应着一个复数的半周期ω2 = -ω1 - ω3 。这三个半周期通过方程与对应的三个根
e
i
{\displaystyle e_{i}}
i
{\displaystyle i}
φ
0
{\displaystyle \varphi _{0}}
ζ
{\displaystyle \zeta }
近星点 或远星点 :
d
ζ
d
ϕ
=
0
w
h
e
n
ζ
=
℘
(
−
ω
i
)
=
e
i
{\displaystyle {\frac {d\zeta }{d\phi }}=0\ \mathrm {when} \ \zeta =\wp (-\omega _{i})=e_{i}}
由于
(
d
ζ
d
φ
)
2
=
G
(
ζ
)
=
4
ζ
3
−
g
2
ζ
−
g
3
=
4
(
ζ
−
e
1
)
(
ζ
−
e
2
)
(
ζ
−
e
3
)
,
{\displaystyle \left({\frac {d\zeta }{d\varphi }}\right)^{2}=G(\zeta )=4\zeta ^{3}-g_{2}\zeta -g_{3}=4\left(\zeta -e_{1}\right)\left(\zeta -e_{2}\right)\left(\zeta -e_{3}\right),}
可以看到
ζ
{\displaystyle \zeta }
e
i
{\displaystyle e_{i}}
导数 的值为零。
不同轨道的定性性质取决于
φ
0
{\displaystyle \varphi _{0}}
φ
0
{\displaystyle \varphi _{0}}
ω
2
{\displaystyle \omega _{2}}
ζ
=
e
2
{\displaystyle \zeta =e_{2}}
ζ
=
e
3
{\displaystyle \zeta =e_{3}}
ζ
=
−
1
/
12
{\displaystyle \zeta =-1/12}
φ
0
{\displaystyle \varphi _{0}}
ω
1
{\displaystyle \omega _{1}}
ζ
{\displaystyle \zeta }
e
1
{\displaystyle e_{1}}
在系统能量满足不等式E 2 < m 2 c 4 的前提下,
φ
0
{\displaystyle \varphi _{0}}
ω
2
{\displaystyle \omega _{2}}
ζ
=
℘
(
ϕ
−
ϕ
0
)
{\displaystyle \zeta =\wp (\phi -\phi _{0})}
ζ
{\displaystyle \zeta }
ζ
{\displaystyle \zeta }
e
3
{\displaystyle e_{3}}
e
2
{\displaystyle e_{2}}
ζ
{\displaystyle \zeta }
进动 的椭圆轨道,当粒子(或行星)从起始状态开始演化时,其半径在最小半径
r
m
i
n
{\displaystyle r_{min}}
r
m
a
x
{\displaystyle r_{max}}
[ 16] :714
r
m
i
n
=
3
r
s
1
+
12
e
2
{\displaystyle r_{min}={\frac {3r_{s}}{1+12e_{2}}}}
r
m
a
x
=
3
r
s
1
+
12
e
1
{\displaystyle r_{max}={\frac {3r_{s}}{1+12e_{1}}}}
它们分别对应着
ζ
{\displaystyle \zeta }
魏尔施特拉斯椭圆函数 的实数周期为
2
ω
1
{\displaystyle 2\omega _{1}}
2
ω
1
{\displaystyle 2\omega _{1}}
2
ω
1
{\displaystyle 2\omega _{1}}
2
π
{\displaystyle 2\pi }
这是2e 2 = 2e 3 = −e 1 的特殊情形,即方程
G
(
ζ
)
{\displaystyle G(\zeta )}
ζ
{\displaystyle \zeta }
e = e 2 = e 4 ,这个解对应着经典的圆轨道,即上面得到的半径为
r
o
u
t
e
r
{\displaystyle r_{outer}}
r
o
u
t
e
r
{\displaystyle r_{outer}}
3
r
s
{\displaystyle 3r_{s}}
轨道半径趋于无穷大对应着粒子飞向无限远处,这时
ζ
{\displaystyle \zeta }
e 2 ≤ −1/12 ≤ ζ ≤ e 3 。
当-e 3 = 2e 2 = 2e 1 ,
ζ
{\displaystyle \zeta }
e 3 是负值。将重根代换为
e
=
n
2
/
3
{\displaystyle e=n^{2}/3}
φ
{\displaystyle \varphi }
ζ
=
r
s
4
r
−
1
12
=
e
−
n
2
cosh
2
n
φ
.
{\displaystyle \zeta ={\frac {r_{s}}{4r}}-{\frac {1}{12}}=e-{\frac {n^{2}}{\cosh ^{2}n\varphi }}.}
可以将这个解代回方程验证。当
φ
{\displaystyle \varphi }
r
s
4
r
−
1
12
=
e
.
{\displaystyle {\frac {r_{s}}{4r}}-{\frac {1}{12}}=e.}
在这种情形下,粒子的轨道半径一定处于
2
r
s
{\displaystyle 2r_{s}}
3
r
s
{\displaystyle 3r_{s}}
渐近的圆轨道也可以通过用雅可比椭圆函数 来表示魏尔施特拉斯椭圆函数得到:
ζ
=
℘
(
ϕ
−
ϕ
0
)
=
e
1
+
(
e
1
−
e
3
)
c
n
2
w
s
n
2
w
{\displaystyle \zeta =\wp (\phi -\phi _{0})=e_{1}+\left(e_{1}-e_{3}\right){\frac {\mathrm {cn} ^{2}w}{\mathrm {sn} ^{2}w}}}
这里
w
=
(
ϕ
−
ϕ
0
)
e
1
−
e
3
{\displaystyle w=(\phi -\phi _{0}){\sqrt {e_{1}-e_{3}}}}
k
=
e
2
−
e
3
e
1
−
e
3
{\displaystyle k={\sqrt {\frac {e_{2}-e_{3}}{e_{1}-e_{3}}}}}
在e 2 趋于e 1 的极限下,模数趋于1,而
w
{\displaystyle w}
n
(
φ
−
φ
0
)
{\displaystyle n(\varphi -\varphi _{0})}
φ
0
{\displaystyle \varphi _{0}}
i
k
′
{\displaystyle ik^{\prime }}
当
φ
0
{\displaystyle \varphi _{0}}
ω
1
{\displaystyle \omega _{1}}
ζ
{\displaystyle \zeta }
ζ
{\displaystyle \zeta }
e 1 ,这使得轨道方程
(
d
ζ
d
φ
)
2
=
4
ζ
3
−
g
2
ζ
−
g
3
=
4
(
ζ
−
e
1
)
(
ζ
−
e
2
)
(
ζ
−
e
3
)
{\displaystyle \left({\frac {d\zeta }{d\varphi }}\right)^{2}=4\zeta ^{3}-g_{2}\zeta -g_{3}=4\left(\zeta -e_{1}\right)\left(\zeta -e_{2}\right)\left(\zeta -e_{3}\right)}
对于所有大于e 1 的
ζ
{\displaystyle \zeta }
ζ
{\displaystyle \zeta }
r
=
0
{\displaystyle r=0}
实验上观测到的脉冲双星PSR B1913+16的轨道周期变化(图中蓝色的点)和广义相对论的理论预测(图中黑色的曲线)完全吻合 根据广义相对论,两个互相绕转的质量例如双星系统 会发出引力辐射,由引力辐射携带的能量会让它们的轨道稍微偏离测地线方程所得到的结果。关于这一问题的最著名间接验证是由拉塞尔·赫尔斯 和约瑟夫·泰勒 对一个脉冲双星PSR B1913+16的观测,两人因此获得1993年的诺贝尔物理学奖 。系统内的两颗中子星 距离非常接近,且绕转速度非常之快,测量到的一个周期时长大约仅为465分钟。两颗中子星的轨道是高度椭圆的,偏心率达到0.62。按照广义相对论的预言,这样短的轨道周期和高度的偏心轨道使得这个双星系统成为一个非常好的引力波源,通过引力辐射损失的能量使轨道逐渐衰减,轨道周期逐渐变短。通过长达三十年的实验观测,即使是在可以达到的最精确的测量下轨道周期的降低和广义相对论的预言仍符合得相当好。广义相对论还预言,再过三亿年后这两颗恒星最终会碰撞到一起。
开普勒问题中因引力辐射导致的能量和角动量 的损耗公式已经通过计算得到[ 17] [ 12] :356-357
−
⟨
d
E
d
t
⟩
=
32
G
4
m
1
2
m
2
2
(
m
1
+
m
2
)
5
c
5
a
5
(
1
−
e
2
)
7
/
2
(
1
+
73
24
e
2
+
37
96
e
4
)
{\displaystyle -\langle {\frac {dE}{dt}}\rangle ={\frac {32G^{4}m_{1}^{2}m_{2}^{2}\left(m_{1}+m_{2}\right)}{5c^{5}a^{5}\left(1-e^{2}\right)^{7/2}}}\left(1+{\frac {73}{24}}e^{2}+{\frac {37}{96}}e^{4}\right)}
这里e是椭圆轨道的偏心率,a是半长轴。方程左边的角括号表示是在一个轨道周期内取平均值。类似的,角动量的平均变化率为
−
⟨
d
L
z
d
t
⟩
=
32
G
7
/
2
m
1
2
m
2
2
m
1
+
m
2
5
c
5
a
7
/
2
(
1
−
e
2
)
2
(
1
+
7
8
e
2
)
{\displaystyle -\langle {\frac {dL_{z}}{dt}}\rangle ={\frac {32G^{7/2}m_{1}^{2}m_{2}^{2}{\sqrt {m_{1}+m_{2}}}}{5c^{5}a^{7/2}\left(1-e^{2}\right)^{2}}}\left(1+{\frac {7}{8}}e^{2}\right)}
周期减少率
P
b
{\displaystyle P_{b}}
[ 17] [ 18]
−
⟨
d
P
b
d
t
⟩
=
192
G
5
/
3
m
1
m
2
(
m
1
+
m
2
)
−
1
/
3
5
c
5
(
1
−
e
2
)
7
/
2
(
1
+
73
24
e
2
+
37
96
e
4
)
(
P
b
2
π
)
−
5
/
3
{\displaystyle -{\Bigl \langle }{\frac {dP_{b}}{dt}}{\Bigr \rangle }={\frac {192G^{5/3}m_{1}m_{2}\left(m_{1}+m_{2}\right)^{-1/3}}{5c^{5}\left(1-e^{2}\right)^{7/2}}}\left(1+{\frac {73}{24}}e^{2}+{\frac {37}{96}}e^{4}\right)({\frac {P_{b}}{2\pi }})^{-5/3}}
轨道的偏心率越接近于1,即椭圆轨道形状越瘦长时,能量和角动量的损耗就越快;而半长轴越短轨道的衰减也越快
开普勒运动的轨道方程也可以通过哈密顿-雅可比方程 推导出。这种方法的好处是它可以将一个粒子的运动等价于一束波的传播,这就很容易进而通过费马原理 推导出光线在引力场中的偏折公式。这种方法的解释是,由于引力场的延时效应,一束波的波前靠近中心质量
m
{\displaystyle m}
使用一般的协变性 ,一个粒子在任意坐标下的哈密顿-雅可比方程可以表示为[ 19] :649,1188 [ 12] :328-330
g
μ
ν
∂
S
∂
x
μ
∂
S
∂
x
ν
=
m
2
c
2
.
{\displaystyle g^{\mu \nu }{\frac {\partial S}{\partial x^{\mu }}}{\frac {\partial S}{\partial x^{\nu }}}=m^{2}c^{2}.}
特别地,在史瓦西度规下
1
c
2
(
1
−
r
s
r
)
(
∂
S
∂
t
)
2
−
(
1
−
r
s
r
)
(
∂
S
∂
r
)
2
−
1
r
2
(
∂
S
∂
φ
)
2
=
m
2
c
2
{\displaystyle {\frac {1}{c^{2}\left(1-{\frac {r_{s}}{r}}\right)}}\left({\frac {\partial S}{\partial t}}\right)^{2}-\left(1-{\frac {r_{s}}{r}}\right)\left({\frac {\partial S}{\partial r}}\right)^{2}-{\frac {1}{r^{2}}}\left({\frac {\partial S}{\partial \varphi }}\right)^{2}=m^{2}c^{2}}
这里我们仍然选取了轨道平面位于
θ
=
π
/
2
{\displaystyle \theta =\pi /2}
球坐标系 。假设哈密顿主函数
S
{\displaystyle S}
可分离变量 的,则其应具有如下形式:
S
=
−
E
t
+
L
φ
+
S
r
(
r
)
{\displaystyle S=-Et+L\varphi +S_{r}(r)}
这里
E
{\displaystyle E}
L
{\displaystyle L}
S
r
(
r
)
{\displaystyle S_{r}(r)}
S
r
(
r
)
=
∫
L
d
r
1
−
r
s
r
1
b
2
−
(
1
−
r
s
r
)
(
1
a
2
+
1
r
2
)
.
{\displaystyle S_{r}(r)=\int {\frac {Ldr}{1-{\frac {r_{s}}{r}}}}{\sqrt {{\frac {1}{b^{2}}}-\left(1-{\frac {r_{s}}{r}}\right)\left({\frac {1}{a^{2}}}+{\frac {1}{r^{2}}}\right)}}.}
对这个主函数求偏导数 :
∂
S
∂
L
=
φ
+
∂
S
r
∂
L
=
c
o
n
s
t
a
n
t
{\displaystyle {\frac {\partial S}{\partial L}}=\varphi +{\frac {\partial S_{r}}{\partial L}}=\mathrm {constant} }
将满足上面得到的轨道方程
(
d
r
d
φ
)
2
=
r
4
b
2
−
(
1
−
r
s
r
)
(
r
4
a
2
+
r
2
)
.
{\displaystyle \left({\frac {dr}{d\varphi }}\right)^{2}={\frac {r^{4}}{b^{2}}}-\left(1-{\frac {r_{s}}{r}}\right)\left({\frac {r^{4}}{a^{2}}}+r^{2}\right).}
这种方法也可以精致地推导出轨道的进动率。
在质量趋于零(或
a
{\displaystyle a}
S
r
(
r
)
=
E
c
∫
d
r
r
2
(
r
−
r
s
)
2
−
b
2
r
(
r
−
r
s
)
{\displaystyle S_{r}(r)={\frac {E}{c}}\int dr{\sqrt {{\frac {r^{2}}{\left(r-r_{s}\right)^{2}}}-{\frac {b^{2}}{r\left(r-r_{s}\right)}}}}}
从这个公式可以导出光线在引力场中的偏振公式。
在广义相对论中,无质量粒子在时空中的运动轨迹是测地线 ,这是等效原理 的要求。从最小作用量原理 的观点来看,测地线长度的变分 为零,即:[ 12] :263-264
0
=
δ
s
=
δ
∫
d
s
=
δ
∫
g
μ
ν
d
x
μ
d
τ
d
x
ν
d
τ
d
τ
=
δ
∫
2
T
d
τ
{\displaystyle 0=\delta s=\delta \int ds=\delta \int {\sqrt {g_{\mu \nu }{\frac {dx^{\mu }}{d\tau }}{\frac {dx^{\nu }}{d\tau }}}}d\tau =\delta \int {\sqrt {2T}}d\tau }
这里
τ
{\displaystyle \tau }
s
=
c
τ
{\displaystyle s=c\tau }
T
{\displaystyle T}
2
T
=
c
2
=
(
d
s
d
τ
)
2
=
g
μ
ν
d
x
μ
d
τ
d
x
ν
d
τ
=
(
1
−
r
s
r
)
c
2
(
d
t
d
τ
)
2
−
1
1
−
r
s
r
(
d
r
d
τ
)
2
−
r
2
(
d
φ
d
τ
)
2
{\displaystyle 2T=c^{2}=\left({\frac {ds}{d\tau }}\right)^{2}=g_{\mu \nu }{\frac {dx^{\mu }}{d\tau }}{\frac {dx^{\nu }}{d\tau }}=\left(1-{\frac {r_{s}}{r}}\right)c^{2}\left({\frac {dt}{d\tau }}\right)^{2}-{\frac {1}{1-{\frac {r_{s}}{r}}}}\left({\frac {dr}{d\tau }}\right)^{2}-r^{2}\left({\frac {d\varphi }{d\tau }}\right)^{2}}
其物理意义类似于经典力学中的动能。如果将时空坐标的四维分量对固有时的导数写成
x
˙
μ
=
d
x
μ
d
τ
{\displaystyle {\dot {x}}^{\mu }={\frac {dx^{\mu }}{d\tau }}}
则
T
{\displaystyle T}
[ 16] :708-709
2
T
=
c
2
=
(
1
−
r
s
r
)
c
2
(
t
˙
)
2
−
1
1
−
r
s
r
(
r
˙
)
2
−
r
2
(
φ
˙
)
2
{\displaystyle 2T=c^{2}=\left(1-{\frac {r_{s}}{r}}\right)c^{2}\left({\dot {t}}\right)^{2}-{\frac {1}{1-{\frac {r_{s}}{r}}}}\left({\dot {r}}\right)^{2}-r^{2}\left({\dot {\varphi }}\right)^{2}}
常数因数的引入对变分问题的结果不会造成影响,因此在积分内取变分仍满足哈密顿原理 :
0
=
δ
∫
2
T
d
τ
=
∫
δ
T
2
T
d
τ
=
1
c
δ
∫
T
d
τ
.
{\displaystyle 0=\delta \int {\sqrt {2T}}d\tau =\int {\frac {\delta T}{\sqrt {2T}}}d\tau ={\frac {1}{c}}\delta \int Td\tau .}
从拉格朗日方程 可以得到变分问题的解
d
d
τ
(
∂
T
∂
x
˙
σ
)
=
∂
T
∂
x
σ
.
{\displaystyle {\frac {d}{d\tau }}\left({\frac {\partial T}{\partial {\dot {x}}^{\sigma }}}\right)={\frac {\partial T}{\partial x^{\sigma }}}.}
对变量
t
{\displaystyle t}
φ
{\displaystyle \varphi }
d
d
τ
[
r
2
d
φ
d
τ
]
=
0
,
{\displaystyle {\frac {d}{d\tau }}\left[r^{2}{\frac {d\varphi }{d\tau }}\right]=0,}
d
d
τ
[
(
1
−
r
s
r
)
d
t
d
τ
]
=
0
,
{\displaystyle {\frac {d}{d\tau }}\left[\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\right]=0,}
进一步可写成
L
{\displaystyle L}
E
{\displaystyle E}
r
2
d
φ
d
τ
=
L
m
,
{\displaystyle r^{2}{\frac {d\varphi }{d\tau }}={\frac {L}{m}},}
(
1
−
r
s
r
)
d
t
d
τ
=
E
m
c
2
.
{\displaystyle \left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}={\frac {E}{mc^{2}}}.}
这也是上面看到的从史瓦西度规直接得到的结果。
只受到引力作用的粒子的作用量 为[ 16] :313ff
S
=
∫
−
m
c
2
d
τ
=
−
m
c
∫
c
d
τ
d
q
d
q
=
−
m
c
∫
g
μ
ν
d
x
μ
d
q
d
x
ν
d
q
d
q
{\displaystyle S=\int {-mc^{2}d\tau }=-mc\int {c{\frac {d\tau }{dq}}dq}=-mc\int {{\sqrt {g_{\mu \nu }{\frac {dx^{\mu }}{dq}}{\frac {dx^{\nu }}{dq}}}}dq}}
其中
q
{\displaystyle q}
世界线 可微化的参数,对这个作用量使用变分法就可以得到测地线方程。不过如果我们对被积函数的平方求变分过程会更简单,根据度规这个平方的形式为
(
c
d
τ
d
q
)
2
=
g
μ
ν
d
x
μ
d
q
d
x
ν
d
q
=
(
1
−
r
s
r
)
c
2
(
d
t
d
q
)
2
−
1
1
−
r
s
r
(
d
r
d
q
)
2
−
r
2
(
d
φ
d
q
)
2
{\displaystyle \left(c{\frac {d\tau }{dq}}\right)^{2}=g_{\mu \nu }{\frac {dx^{\mu }}{dq}}{\frac {dx^{\nu }}{dq}}=\left(1-{\frac {r_{s}}{r}}\right)c^{2}\left({\frac {dt}{dq}}\right)^{2}-{\frac {1}{1-{\frac {r_{s}}{r}}}}\left({\frac {dr}{dq}}\right)^{2}-r^{2}\left({\frac {d\varphi }{dq}}\right)^{2}}
取变分
δ
(
c
d
τ
d
q
)
2
=
2
c
2
d
τ
d
q
δ
d
τ
d
q
=
δ
[
(
1
−
r
s
r
)
c
2
(
d
t
d
q
)
2
−
1
1
−
r
s
r
(
d
r
d
q
)
2
−
r
2
(
d
φ
d
q
)
2
]
{\displaystyle \delta \left(c{\frac {d\tau }{dq}}\right)^{2}=2c^{2}{\frac {d\tau }{dq}}\delta {\frac {d\tau }{dq}}=\delta \left[\left(1-{\frac {r_{s}}{r}}\right)c^{2}\left({\frac {dt}{dq}}\right)^{2}-{\frac {1}{1-{\frac {r_{s}}{r}}}}\left({\frac {dr}{dq}}\right)^{2}-r^{2}\left({\frac {d\varphi }{dq}}\right)^{2}\right]}
如果我们只对
φ
{\displaystyle \varphi }
2
c
2
d
τ
d
q
δ
d
τ
d
q
=
−
2
r
2
d
φ
d
q
δ
d
φ
d
q
{\displaystyle 2c^{2}{\frac {d\tau }{dq}}\delta {\frac {d\tau }{dq}}=-2r^{2}{\frac {d\varphi }{dq}}\delta {\frac {d\varphi }{dq}}}
两边除以
2
c
d
τ
d
q
{\displaystyle 2c{\frac {d\tau }{dq}}}
c
δ
d
τ
d
q
=
−
r
2
c
d
φ
d
τ
δ
d
φ
d
q
=
−
r
2
c
d
φ
d
τ
d
δ
φ
d
q
{\displaystyle c\delta {\frac {d\tau }{dq}}=-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\delta {\frac {d\varphi }{dq}}=-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}{\frac {d\delta \varphi }{dq}}}
代入哈密顿原理的方程
0
=
δ
∫
c
d
τ
d
q
d
q
=
∫
c
δ
d
τ
d
q
d
q
=
∫
−
r
2
c
d
φ
d
τ
d
δ
φ
d
q
d
q
{\displaystyle 0=\delta \int {c{\frac {d\tau }{dq}}dq}=\int {c\delta {\frac {d\tau }{dq}}dq}=\int {-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}{\frac {d\delta \varphi }{dq}}dq}}
通过分部积分法
0
=
−
r
2
c
d
φ
d
τ
δ
φ
−
∫
d
d
q
[
−
r
2
c
d
φ
d
τ
]
δ
φ
d
q
{\displaystyle 0=-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\delta \varphi -\int {{\frac {d}{dq}}\left[-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\right]\delta \varphi dq}}
在端点处纬度的变分为零,因此等式右边第一项为零;对于第二项,由于
δ
φ
{\displaystyle \delta \varphi }
d
d
q
[
−
r
2
c
d
φ
d
τ
]
=
0
{\displaystyle {\frac {d}{dq}}\left[-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\right]=0}
如果我们只对
t
{\displaystyle t}
2
c
2
d
τ
d
q
δ
d
τ
d
q
=
2
(
1
−
r
s
r
)
c
2
d
t
d
q
δ
d
t
d
q
{\displaystyle 2c^{2}{\frac {d\tau }{dq}}\delta {\frac {d\tau }{dq}}=2\left(1-{\frac {r_{s}}{r}}\right)c^{2}{\frac {dt}{dq}}\delta {\frac {dt}{dq}}}
类似地,两边除以
2
c
d
τ
d
q
{\displaystyle 2c{\frac {d\tau }{dq}}}
c
δ
d
τ
d
q
=
c
(
1
−
r
s
r
)
d
t
d
τ
δ
d
t
d
q
=
c
(
1
−
r
s
r
)
d
t
d
τ
d
δ
t
d
q
{\displaystyle c\delta {\frac {d\tau }{dq}}=c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\delta {\frac {dt}{dq}}=c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}{\frac {d\delta t}{dq}}}
根据哈密顿原理
0
=
δ
∫
c
d
τ
d
q
d
q
=
∫
c
(
1
−
r
s
r
)
d
t
d
τ
d
δ
t
d
q
d
q
{\displaystyle 0=\delta \int {c{\frac {d\tau }{dq}}dq}=\int {c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}{\frac {d\delta t}{dq}}dq}}
分部积分
0
=
c
(
1
−
r
s
r
)
d
t
d
τ
δ
t
−
∫
d
d
q
[
c
(
1
−
r
s
r
)
d
t
d
τ
]
δ
t
d
q
{\displaystyle 0=c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\delta t-\int {{\frac {d}{dq}}\left[c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\right]\delta tdq}}
得到运动方程
d
d
q
[
c
(
1
−
r
s
r
)
d
t
d
τ
]
=
0
{\displaystyle {\frac {d}{dq}}\left[c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\right]=0}
对这两个方程积分并指定积分常数就可以得到上面关于守恒量的方程
r
2
d
φ
d
τ
=
L
m
,
{\displaystyle r^{2}{\frac {d\varphi }{d\tau }}={\frac {L}{m}},}
(
1
−
r
s
r
)
d
t
d
τ
=
E
m
c
2
.
{\displaystyle \left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}={\frac {E}{mc^{2}}}.}
对于能量和角动量是常数的系统,这两个方程可以合并为一个并且对光子这样的无质量粒子同样成立,此时沿着所描述的测地线的固有时总为零。
r
2
b
c
d
φ
d
t
=
1
−
r
s
r
{\displaystyle {\frac {r^{2}}{bc}}{\frac {d\varphi }{dt}}=1-{\frac {r_{s}}{r}}}
^ 克里斯托费尔符号以方程表示为
Γ
k
l
i
=
1
2
g
i
m
(
∂
g
m
k
∂
x
l
+
∂
g
m
l
∂
x
k
−
∂
g
k
l
∂
x
m
)
{\displaystyle \Gamma _{kl}^{i}={\frac {1}{2}}g^{im}\left({\frac {\partial g_{mk}}{\partial x^{l}}}+{\frac {\partial g_{ml}}{\partial x^{k}}}-{\frac {\partial g_{kl}}{\partial x^{m}}}\right)}
^ Le Verrier, UJJ . Unknown title. Comptes Revues d'Academie de la Science de Paris. 1859, 49 : 379–?. ^ 2.0 2.1 2.2 Pais, A. Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. 1982. ISBN 0-19-520438-7 . ^ Sergei Kopeikin; Michael Efroimsky; George Kaplan. Relativistic Celestial Mechanics of the Solar System. John Wiley & Sons. 25 October 2011. ISBN 978-3-527-63457-6 ^ Einstein, A., Relativitätsprinzip und die aus demselben gezogenen Folgerungen (On the Relativity Principle and the Conclusions Drawn from It), Jahrbuch der Radioaktivität (Yearbook of Radioactivity): 411–462 ^ Janssen, Michel, Of pots and holes: Einstein's bumpy road to general relativity , Ann. Phys. (Leipzig), 2005, 14 (S1): 58–85 [2014-03-14 ] , Bibcode:2005AnP...517S..58J doi:10.1002/andp.200410130 原始内容 (PDF) 存档于2020-08-25) ^ Kennefick, Daniel, Astronomers Test General Relativity: Light-bending and the Solar Redshift, Renn, Jürgen (编), Albert Einstein: One hundred authors for Einstein, Wiley-VCH: 178–181, 2005, ISBN 3-527-40574-7 ^ Heinbockel, J. H., Introduction to Tensor Calculus and Continuum Mechanics , Trafford Publishing, 2001 [2014-03-14 ] , ISBN 978-1553691334原始内容 存档于2020-01-06) ^ 8.0 8.1 8.2 8.3 8.4 Taylor, edwin; John Wheeler, Edmund Bertschinger, Exploring Black Holes: Introduction to General Relativity 2nd, Pearson College Div, 2011, ISBN 9780321512864 ^ Weinberg, S. Gravitation and Cosmology . New York: John Wiley and Sons. 1972. ISBN 978-0-471-92567-5
^ 10.0 10.1 10.2 10.3 10.4 Bernard Schutz. A First Course in General Relativity . Cambridge University Press. 14 May 2009. ISBN 978-0-521-88705-2 ^ Whittaker, ET. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, with an Introduction to the Problem of Three Bodies 4th ed. New York: Dover Publications. 1937: pp. 389–393. ISBN 978-1-114-28944-4 ^ 12.0 12.1 12.2 12.3 Landau, LD; Lifshitz, EM. The Classical Theory of Fields (Course of Theoretical Physics, Vol. 2) revised 4th English ed. New York: Pergamon Press. 1975. ISBN 978-0-08-018176-9 ^ Brown, Kevin. Bending Light . Reflections on Relativity. [Mar 15, 2014] . (- 6.3 原始内容 存档于2014-07-31). ^ John Earman; Michel Janssen; John D. Norton. The Attraction of Gravitation: New Studies in the History of General Relativity. Springer. 1 December 1993. ISBN 978-0-8176-3624-1 ^ Goldstein, Herbert, Classical Mechanics 3rd, United States of America: Addison Wesley, 1980, ISBN 0201657023(英语) ^ 16.0 16.1 16.2 16.3 16.4 Gerd Baumann. Mathematica for Theoretical Physics: Electrodynamics, Quantum Mechanics, General Relativity, and Fractals . Springer. 16 January 2006 [2014-03-16 ] . ISBN 978-0-387-25113-4存档 于2014-06-30). ^ 17.0 17.1 Peters PC, Mathews J. Gravitational Radiation from Point Masses in a Keplerian Orbit. Physical Review. 1963, 131 : 435–440. Bibcode:1963PhRv..131..435P doi:10.1103/PhysRev.131.435 ^ Weisberg, J.M.; Taylor, J.H. The Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis . F.A. Rasio and I.H. Stairs (eds.) (编). ASP Conference Series 328 . Aspen, Colorado, USA: Astronomical Society of the Pacific: 25. July 2005 [2014-03-16 ] . Bibcode:2005ASPC..328...25W arXiv:astro-ph/0407149 存档 于2011-07-25). ^ J.A. Wheeler, C. Misner, K.S. Thorne. Gravitation. W.H. Freeman & Co. 1973. ISBN 0-7167-0344-0
Hagihara, Y. Theory of the relativistic trajectories in a gravitational field of Schwarzschild. Japanese Journal of Astronomy and Geophysics. 1931, 8 : 67–176. ISSN 0368-346X
基础概念 现象 方程 进阶理论 精确解 近似解与数值模拟 科学家




 . (原始内容存档于2011-07-25).
. (原始内容存档于2011-07-25).




















































![{\displaystyle {\frac {1}{2}}m\left({\frac {dr}{d\tau }}\right)^{2}=\left[{\frac {E^{2}}{2mc^{2}}}-{\frac {1}{2}}mc^{2}\right]+{\frac {GMm}{r}}-{\frac {L^{2}}{2mr^{2}}}+{\frac {GML^{2}}{c^{2}mr^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5318d7d3eb4d8c6b9e66dbf0effffc5297383e75)










![{\displaystyle V(r)={\frac {mc^{2}}{2}}\left[-{\frac {r_{s}}{r}}+{\frac {a^{2}}{r^{2}}}-{\frac {r_{s}a^{2}}{r^{3}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1dc9d62dd01e10253063b8383c4cd9b055d5d27)
![{\displaystyle F=-{\frac {dV}{dr}}=-{\frac {mc^{2}}{2r^{4}}}\left[r_{s}r^{2}-2a^{2}r+3r_{s}a^{2}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d88f2da9ae5e8b7b5bd74690d22f4996401b536c)














![{\displaystyle \omega _{r}^{2}={\frac {1}{m}}\left[{\frac {d^{2}V}{dr^{2}}}\right]_{r=r_{\mathrm {outer} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/894cef5f743b66cd47bfe665608a9fff3e703799)












































































![{\displaystyle {\frac {d}{d\tau }}\left[r^{2}{\frac {d\varphi }{d\tau }}\right]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e7587be0611673e3ad751e0db29a70635d76108)
![{\displaystyle {\frac {d}{d\tau }}\left[\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\right]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e43df66c44d864551699f249c91284633e11a414)


![{\displaystyle \delta \left(c{\frac {d\tau }{dq}}\right)^{2}=2c^{2}{\frac {d\tau }{dq}}\delta {\frac {d\tau }{dq}}=\delta \left[\left(1-{\frac {r_{s}}{r}}\right)c^{2}\left({\frac {dt}{dq}}\right)^{2}-{\frac {1}{1-{\frac {r_{s}}{r}}}}\left({\frac {dr}{dq}}\right)^{2}-r^{2}\left({\frac {d\varphi }{dq}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aca95a35ae6a9911e1399bd759b8ad167d4cffd)




![{\displaystyle 0=-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\delta \varphi -\int {{\frac {d}{dq}}\left[-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\right]\delta \varphi dq}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a396d0dc7e209a343b1633faeaa37953cb250d63)

![{\displaystyle {\frac {d}{dq}}\left[-{\frac {r^{2}}{c}}{\frac {d\varphi }{d\tau }}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8da37d5aeba3fee4873426b62835abfb109cda2a)



![{\displaystyle 0=c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\delta t-\int {{\frac {d}{dq}}\left[c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\right]\delta tdq}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb9416a3e0124397cc488193c1d4cd41e2c81dcd)
![{\displaystyle {\frac {d}{dq}}\left[c\left(1-{\frac {r_{s}}{r}}\right){\frac {dt}{d\tau }}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9493bddcfc4668a0946abc50b36949dfe5e472f5)

