單子 (範疇論)

  关于單子在電腦軟件的應用，请见「單子 (函數式編程)」。

數學的分支範疇論中，單子（英語：monad），又稱三元組（triple, triad）、標準構造（standard construction）、基本構造（fundamental construction），是一個內函子（即由某範疇映到自身的函子），連同滿足特定連貫條件的兩個自然變換，三者構成的整體。單子用於研究互為伴隨的函子對，並將偏序集上的闭包算子推廣到任意範疇。

導論與定義

單子是一類內函子（連同其他資訊）。例如，若$F$和$G$為一對伴隨函子，$F$為$G$的左伴隨，則複合$G\circ F$是單子。若$F$與$G$互為逆函子，則對應的單子是恆等函子。一般而言，伴隨關係並不等同范畴的等价，而可以聯繫不同性質的範疇。為了探討伴隨關係所「保持」的性質，數學家研究單子論。理論的另一半，即藉考慮$F\circ G$，以研究伴隨關係，是單子論的對偶理論。該類函子稱為餘單子（英語：comonad）。

嚴格定義

本條目中，${\mathcal {C}}$皆表示某範疇。${\mathcal {C}}$上的單子是函子$T:{\mathcal {C}}\to {\mathcal {C}}$，連同兩個自然變換，分別是單位$\eta :1_{\mathcal {C}}\to T$（其中$1_{\mathcal {C}}$是${\mathcal {C}}$上的恆等函子）與乘法$\mu :T^{2}\to T$（其中$T^{2}$是複合$T\circ T$，亦是${\mathcal {C}}$到${\mathcal {C}}$的函子），且要滿足下列連貫條件：

• $\mu \circ T\mu =\mu \circ \mu T$（左右皆為$T^{3}\to T$的自然變換）。此處$T\mu$與$\mu T$經水平複合而得。
• $\mu \circ T\eta =\mu \circ \eta T=1_{T}$（兩者皆為$T\to T$的自然變換）。此處$1_{T}$表示由函子$T$到自身的恆等自然變換。

以上兩式，亦可以下列交換圖複述：

記號$T\mu$與$\mu T$的含義，參見自然變換，又或考慮以下更具體的寫法，不用水平複合記號，並將各函子作用在任意物件$X$上：

定義中，若將$\mu$當成幺半群的乘法，則第一條公理類似幺半群的乘法結合律，而第二條公理類似單位元的存在性（由$\eta$給出）。準確而言，${\mathcal {C}}$上的單子，可以等價地定義為${\mathcal {C}}$的內函子範疇$\mathbf {End} _{\mathcal {C}}$中的幺半群。（該範疇的物件是$C$上的內函子，而態射是內函子間的自然變換，幺半結構來自內函子的複合運算。）如此，單子不僅在形式上具有與幺半群相似的公理，甚而單子就是幺半群的特例。

冪集單子

冪集單子${\mathcal {P}}$是集合範疇$\mathbf {Set}$上的單子。其定義中，函子$T$取為冪集運算，即$T(A)$為集合$A$的冪集，而對於函數$f:A\to B$，$T(f)$將$A$的子集映至其像集，即$T(f)(A')=f[A']$。對每個集合$A$，有函數$\eta _{A}:A\to T(A)$，對每個元素$a\in A$映至單元子集$\{a\}$， 並有函數

$\mu _{A}\colon T(T(A))\to T(A),$

將$A$的若干個子集構成的族，映至該些子集的並集。以上是冪集單子的定義。

兩個單子的複合，未必為單子。舉例，冪集單子${\mathcal {P}}$的二次疊代${\mathcal {P}}\circ {\mathcal {P}}$，無法配備單子結構。

餘單子

取上節定義的範疇論對偶，便是餘單子（或餘三元組）的定義。簡單複述，範疇${\mathcal {C}}$上的餘單子，是對偶範疇$C^{\mathrm {op} }$上的單子。所以，餘單子是由${\mathcal {C}}$到${\mathcal {C}}$的某個函子$U$，連同餘單位與餘乘法（英語：counit and comultiplication）兩個自然變換，組成的整體，而三者所要滿足的公理，是將原定義中所有態射反轉方向而得。

單子之於幺半群，如同餘單子之於餘幺半群。每個集合皆是餘幺半群，且僅有唯一一種方式，所以抽象代數中，較少考慮餘幺半群。然而，在線性代數中，向量空間範疇（配備張量積）的餘幺半群較為重要，以餘代數之名為人所知。

術語歷史

單子的概念由羅傑·戈德芒於1958年提出，當時稱為「標準構造」（英語：standard construction）。六七十年代，則常稱為「三元組」。現今常用的英文名稱monad是由桑德斯·麥克蘭恩提出。

例子

伴隨的複合

若有伴隨關係

$F:{\mathcal {C}}\rightleftarrows {\mathcal {D}}:G$

（即$F$為$G$的左伴隨，下同），則由此有${\mathcal {C}}$上的單子。此普遍的構造，取內函子為複合

$T=G\circ F,$

而單位自然變換來自伴隨的單位$\eta :\operatorname {id} _{\mathcal {C}}\to G\circ F$，乘法自然變換源自伴隨的餘單位$\varepsilon$：

$T^{2}=G\circ F\circ G\circ F\xrightarrow {G\circ \varepsilon \circ F} G\circ F=T.$

反之，給定單子，可以明確找回一對伴隨函子，使單子為該對伴隨函子的複合。此構造用到下節定義的$T$代數的艾倫伯格－摩爾範疇$C^{T}$。

兩重對偶

給定域$k$，雙重對偶單子（英語：double dualisation monad）源自伴隨關係

$(-)^{*}:\mathbf {Vect} _{k}\rightleftarrows \mathbf {Vect} _{k}^{op}:(-)^{*},$

其中兩個函子$(-)^{*}$皆將$k$向量空间$V$映至對偶空間$V^{*}:=\operatorname {Hom} (V,k)$，所以對應的單子將向量空間$V$映至雙對偶$V^{**}$。Kock (1970)對此有更廣泛的討論。

偏序集的閉包算子

偏序集$(P,\leq )$可以視為特殊的範疇，任意兩件物件之間有最多一支態射，且$x$到$y$有態射当且仅当偏序中$x\leq y$。於是，偏序集之間的函子，即是保序映射，而伴隨函子對，則組成兩偏序集間的伽罗瓦连接，相應的單子是伽羅華連接的闭包算子。

自由遺忘伴隨

又舉例，設$G$為群範疇$\mathbf {Grp}$至集合范畴$\mathbf {Set}$的遺忘函子，將群映至其基集，又設$F$為自由函子，由$\mathbf {Set}$到$\mathbf {Grp}$，則$F$是$G$的左伴隨。此時，對應的單子$T=G\circ F$的作用是，輸入一個集合$X$，輸出自由群$F(X)$的基集，即字母取自$\{x,x^{-1}:x\in X\}$，且無相鄰兩個字母互為逆元的字串的集合。

該單子的單位變換，由包含映射

$\eta _{X}:X\rightarrow T(X)$

給出，該包含映射將$X$的任意元素，看成僅得一個字元的字串，從而是$T(X)$的元素。最後，單子的乘法

$\mu _{X}:T(T(X))\rightarrow T(X)$

是串接或「壓平」運算，將若干條字串組成的串，映至該串中所有字串前後連接而成的一條字串。至此描述完單子的兩個自然變換。

前述例子中，自由群可以推廣至其他種類的代數結構，即泛代数意義下的任意一簇代數。如此，每類代數定義了集合範疇上的一個單子。更重要的是，該類代數的範疇，可從單子找回，即單子的艾倫伯格－摩爾代數範疇，故單子可視為泛代數之簇的推廣。

另外，尚有一個單子源自伴隨關係。在向量空間範疇$\mathbf {Vect}$上，若$T$表示將向量空間$V$映至其张量代数$T(V)$的內函子，則相應有單位自然變換將$V$嵌入到其张量代数，並有乘法自然變換，在$V$處的分量是態射$T(T(V))\to T(V)$，將張量積之張量積展開化簡。

餘密度單子

只要滿足某些不強的條件，無左伴隨的函子也可以產生單子，稱為餘密度單子。例如，從有限集合範疇$\mathbf {FinSet}$到集合範疇$\mathbf {Set}$的包含函子無法配備左伴隨，但其餘密度單子定義在$\mathbf {Set}$上，將任意集合$X$映至其上所有超滤子的集合$\beta X$。 類似例子見於Leinster (2013)。

單子的代數

参见：F代數和偽代數

給定範疇${\mathcal {C}}$上的單子$(T,\eta ,\mu )$，可以考慮${\mathcal {C}}$中的${\boldsymbol {T}}$代數物件。$T$在該些物件上的作用，與單子的單位與乘法相容。具體而言，${\boldsymbol {T}}$代數$(x,h)$是${\mathcal {C}}$中的物件$x$，連同態射$h:Tx\to x$（稱為該代數的結構映射），使得圖

及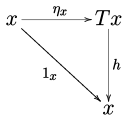

皆可交換。

$T$代數間的態射$f:(x,h)\to (x',h')$是${\mathcal {C}}$中的態射$f:x\to x'$，且要使

可交換。於是，$T$代數及之間的態射組成範疇，稱為艾倫伯格－摩爾範疇（英語：Eilenberg–Moore category），記為${\mathcal {C}}^{T}$.

例子

自由群單子上的代數

若$T$為前述自由群單子，則$T$代數是集合$X$，連同由$X$生成的自由群$F(X)$到$X$的映射（求值，evaluation），且該映射要滿足結合律與單位元的公理。換言之，$X$本身就具有群結構，而$F(X)$至$X$的映射，是將字串按$X$的群乘法，計算所得的結果

分佈單子上的代數

另一個例子是集合範疇上的分佈單子（英語：distribution monad）${\mathcal {D}}$，其將集合$X$映至其上所有有限支撐的概率分佈的集合。該等分佈，是函數$f:X\to [0,1]$，僅於有限多個元素$x\in X$處取值非零，而各元素處取值之和為$1$。以符號表示，

${\mathcal {D}}(X)=\left\{f:X\to [0,1]:{\begin{matrix}\#{\text{supp}}(f)<+\infty ,\\\sum _{x\in X}f(x)=1\end{matrix}}\right\}.$

可由定義證明，分佈單子上的代數，等同於凸集，即集合要配備二元運算$+_{r}$（對每個$r\in [0,1]$），滿足的公理比照歐氏空間中，凸組合$(x,y)\mapsto rx+(1-r)y$具備的性質。