一元一次方程式也被稱為线性方程,因為在笛卡尔坐标系上任何一個一次方程的圖形都是一條直线。组成一次方程的每一项必須是常数或者是一个常數和一个变量的乘積。且方程中必須包含一个變量,因為如果没有變量只有常數,式子則是代数式而非方程式。[1]
如果一次方程式中只包含一个文字符號,且最高次方為一,那么该方程就是一元一次方程式; 如果包含两个文字符號,且最高次方為一,那么就是二元一次方程式;以此類推。
一元一次方程[编辑]
一元一次方程是指一个方程中仅含有一个变量(亦即未知数),且等号两边至少有一个一次单项式,且未知数的指数为 。
。
任意一个一元一次方程皆能化成 (
( )的形式,它的解为
)的形式,它的解为 。以下是一个例子:
。以下是一个例子:

它的解法是
 (移项后合并同类项)
(移项后合并同类项) (两边同除以
(两边同除以 )
)
一元一次方程是一个线性方程,二次项 或二次以上的项是不容许出现的。
或二次以上的项是不容许出现的。
公式

注意:当  时,
时,
 不是一元一次方程。
不是一元一次方程。
 可以推出
可以推出 。
如果
。
如果  ,此方程式无解;如果
,此方程式无解;如果  ,则此方程式有无限多解。
,则此方程式有无限多解。
二元一次方程组[编辑]
求解二元一次方程组可以使用代入消元法或加减消元法。
代入消元法[编辑]
代入消元法就是先利用其中一个方程,将含有其中一个未知数的代数式表示另一个未知数。然后代入另一个方程,从而将这组方程转化成解两个一元一次方程的方法。
例如:

解:

得

再代入

即

从而求出

加减消元法[编辑]
加减消元法就是將两个方程相加或相减,从而消去其中一个未知数,从而将这组方程转化成解两个一元一次方程的方法。
通常可以先将其中一方程的两边同时乘以一个不是0的数,使其中一个未知数的系数与另外一个方程对应的系数相同或为相反数,再将两个方程相加或相减。
例如:

把两式相加消去x,即

从而求出

克拉馬法則[编辑]
一次函数,不等式与一次方程的关系[编辑]
一次函数 中,函数图象与x轴的交点的横坐标即为对应
中,函数图象与x轴的交点的横坐标即为对应 的解。
的解。
线性函数与线性化[编辑]
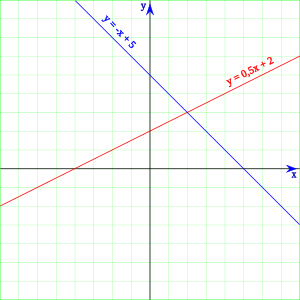 这是一个二元一次方程组的坐标系表示图,蓝线与红线分别各自表示一个二元一次方程式,两线相交处就是这个方程组的解
这是一个二元一次方程组的坐标系表示图,蓝线与红线分别各自表示一个二元一次方程式,两线相交处就是这个方程组的解
在上图的例子中(但不限于此例)变量 是变量
是变量 的函数,我们统一表示为
的函数,我们统一表示为 。函数
。函数 和方程
和方程 的图形一致,二者形成一种对应关系。我们在线性化等问题中习惯将一元一次方程称为线性方程,相应地,我们也把一元一次函数称为线性函数。
的图形一致,二者形成一种对应关系。我们在线性化等问题中习惯将一元一次方程称为线性方程,相应地,我们也把一元一次函数称为线性函数。
线性函数 有如下特性:
有如下特性:


其中 是常数。
是常数。
微分性质:
若线性函数表达式为  (
( ),则
),则  ,
, (
( )。
由此可知,线性函数没有驻点,没有极大值和极小值,且线性函数的斜率就是未知数
)。
由此可知,线性函数没有驻点,没有极大值和极小值,且线性函数的斜率就是未知数  的系数。
的系数。
可以利用线性函数的图形对二元一次方程组进行求解,这类问题就是线性化问题。
參考文獻[编辑]






































