
此條目介紹的是駐點或者一個真實變量的實值函數的臨界點。关于一般概念,请见「
臨界點 (數學)」。关于物理学上流体中速度为零的点,请见「
滞点」。
驻点(英語:Stationary Point)或稳定点在數學,特別在微積分中是指函數在一點处的一階導數為零,该点即函数的驻点。
 y = x + sin(2x) 的圖像
y = x + sin(2x) 的圖像
驻點(紅色)與拐点(藍色),這圖像的驻點都是局部極大值或局部極小值。
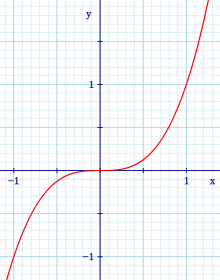 y = x3 的圖像
y = x3 的圖像
原點(0,0)是驻点,但不是局部極值。
也就是說若  為駐點則
為駐點則

在這一點,函數的輸出值停止增加或減少。
对于一维函数的图像,驻点的切线平行于x轴即水平切线。对于二维函数的图像,驻点的切平面平行于xy平面。
值得注意的是,一个函数的驻点不一定是这个函数的极值点[註 1];反过来,在某設定區域內,一个函数的极值点也不一定是这个函数的驻点[註 2],例如函数 。对于可微函数,极值点一定是驻点。
。对于可微函数,极值点一定是驻点。
靜態平衡系統[编辑]
在分析力學裏,虛功原理闡明,對於一個靜態平衡系統,所有外力的作用,經過虛位移,所作的虛功,總合等於零,以方程式表達,
 ;
;
其中, 是虛功,
是虛功, 是第
是第 個外力,
個外力, 是對應於
是對應於 的虛位移。
的虛位移。
轉換為以廣義力 和廣義坐標
和廣義坐標 表達,
表達,
 ;
;
假設這系統是保守系統,則每一個廣義力都是一個純量的廣義位勢函數 的對於其對應的廣義坐標的導數:
的對於其對應的廣義坐標的導數:
 。
。
虛功與廣義位勢的關係為
 。
。
所以,一個靜態平衡系統的位勢 乃是個局域平穩值。注意到這系統只處於平穩狀態。假設,要求這這系統處於穩定狀態,則位勢
乃是個局域平穩值。注意到這系統只處於平穩狀態。假設,要求這這系統處於穩定狀態,則位勢 必須是個局域極小值。
必須是個局域極小值。
歐拉-拉格朗日方程式[编辑]
在變分法裏,歐拉-拉格朗日方程式是從其對應的泛函的平穩點推導出的一種微分方程式。設定
 ,
, ,
, 。
。
若![{\displaystyle \mathbf {y} (x)\in (C^{1}[a,\ b])^{N}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/607d8e0ca154c37911439c327d084fb822f8afcc) 使泛函
使泛函 取得局部平穩值,則在區間
取得局部平穩值,則在區間 內對於所有的
內對於所有的 ,歐拉-拉格朗日方程式成立:
,歐拉-拉格朗日方程式成立:
 。
。






















![{\displaystyle \mathbf {y} (x)\in (C^{1}[a,\ b])^{N}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/607d8e0ca154c37911439c327d084fb822f8afcc)



