曲率

微积分学

$\text{e} = \lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n$

函数 · 导数 · 微分 · 积分 基础概念 函数 · 數列 · 級數 · 极限 初等函数·無窮小量·收敛数列 收斂性 · 夹挤定理 连续 · 一致连续 · 间断点 一元微分 导数 · 高阶导数 · 介值定理 · 中值定理 （罗尔定理 · 拉格朗日中值定理 · 柯西中值定理） · 泰勒公式 · 求导法则 ( 乘法定则 · 除法定则 · 倒数定则 · 链式法则 ) · 洛必达法则 · 导数列表 · 导数的函数应用 ( 单调性 · 极值 · 驻点 · 拐点 · 凹凸性 · 曲率 ) 一元积分 不定积分 · 定积分 · 积分的定义 ( 黎曼积分 · 达布积分 · 勒贝格积分 ) · 积分表 · 求积分的技巧 ( 换元积分法 · 分部积分法 · 三角换元法 · 降次积分法 · 部分分式积分法 ) · 牛顿-莱布尼茨公式 · 广义积分 · 主值 · 柯西主值 · Β函数 · Γ函数 · 数值积分 · 牛顿-寇次公式 · 近似积分法 ( 矩形法 · 梯形法 · 辛普森积分法 ) 多元微积分 多元函数 · 偏导数 · 隐函数 · 全微分 · 方向導數 · 梯度 · 泰勒公式 · 拉格朗日乘数 · 多元函数积分 · 多重积分 · 广义多重积分 · 路径积分 · 曲面积分 · 格林公式 · 高斯公式 · 斯托克斯公式 · 散度 · 旋度 微分方程 常微分方程 · 分离变数法 · 积分因子 · 欧拉方法 · 柯西-欧拉方程 · 伯努利微分方程 · 克莱罗方程 · 全微分方程 · 线性微分方程 · 差分方程 · 拉普拉斯变换法 · 偏微分方程 · 拉普拉斯方程 数学家 牛顿·莱布尼兹·柯西·黎曼 拉格朗日 · 拉普拉斯· 欧拉

曲率是几何体不平坦程度的一种衡量。平坦对不同的几何体有不同的意義。

本文考虑基本的情况，欧几里得空间中的曲线和曲面的曲率。一般意义下的曲率，请参照曲率张量。

平面曲线的曲率

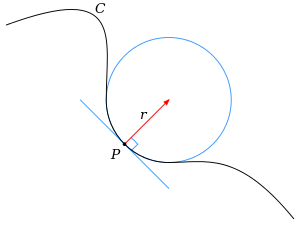曲线 C 在 P 点的密切圆和曲率半径

对于平面曲线 C，在一点P的曲率大小等于密切圆（英语：Osculating circle）半径的倒数，它是一个指向该圆圆心的向量。其大小可用屈光度（dioptre）衡量，1屈光度等于1（弧度）每米。此密切圆的半径即为曲率半径。

密切圆的半径越小，曲率越大；所以曲线接近平直的时候，曲率接近0，而当曲线急速转弯时，曲率很大。

直线曲率处处为0；半径为r的圆曲率处处为1/r。

局部表达式

若曲線 $y = f(x)\,$ 其曲率為

$\kappa= \frac{[{1+f'^2(x)]}^{1/2}f''(x)}{ [{1+f'^2(x)]}^2}$

对于一个以参数化形式给出的平面曲线$c(t) = [x(t),y(t)]\,$ 其曲率为

$\kappa= \frac{[\dot x(t) \ddot y(t) - \ddot x(t) \dot y(t)]\sqrt{\dot x^2(t) + \dot y^2 (t)}}{[\dot x^2(t) + \dot y^2 (t) ]^2}$

其中点表示对 $t\,$的微分。

对于隐式给出的平面曲线$f(x,y)=0\,$ 其曲率为

$\kappa= \nabla\cdot\left(\frac{\nabla f}{\|\nabla f\|}\right)$

也就是，$f\,$的梯度的方向的散度。 最后的公式也给出了在欧几里得空间中的超曲面的平均曲率（可以差一个常数）。

空间曲线的曲率

如果空间曲线的参数方程为 $c(t) = (x(t),y(t),z(t))\,$，

则曲率为：

$F[x,y,z]=\frac{\sqrt{(z''y'-y''z')^2+(x''z'-z''x')^2+(y''x'-x''y')^2}}{(x'^2+y'^2+z'^2)^{3/2}}$

三维空间中的曲面曲率

对于嵌入在欧几里得空间R³中的二维曲面，有两种曲率存在：高斯曲率和平均曲率。为计算在曲面给定点的曲率，考虑曲面和由在该点的法向量和某一切向量所确定的平面的交集。这个交集是一个平面曲线，所以有一个曲率；如果选择其它切向量，这个曲率会改变，并且有两个极值-最大和最小曲率，称为主曲率 k₁ 和k₂，极值方向称为主方向。这里我们采用在曲线向和曲面选定法向的相同方向绕转的时候把曲率置为正数，否则为负的约定。

高斯曲率，以高斯命名，等于主曲率的乘积，k₁k₂. 它的单位为1／长度²，对于球、椭球、双叶双曲面的一叶、椭圆抛物面为正，对于伪球面、 单叶双曲面、双曲抛物面为负，对平面、圆柱面为0。它决定了曲面局部是凸（正的时候）还是局部鞍点（负的时候）。

高斯曲率的以上定义是外在的，因为它用了曲面在 R³中的嵌入，法向量，外部平面等等。但是高斯曲率实际上是曲面的内在属性，也就是它不依赖于曲面的特定嵌入；直观的讲，这意味着活在曲面上的蚂蚁可以确定高斯曲率。形式化的，高斯曲率只依赖于曲面的黎曼度量。这就是高斯著名的絕妙定理，在他在研究地理测绘和地图制作时发现。

高斯曲率在一点P的内在定义的一种：想象一直用一条长为r的短线绑在P。她在线拉直的时候绕P点跑并测量绕P点的一圈的周长C(r)。如果曲面是平的，她会发现 C(r) = 2πr。在弯曲的曲面上，C(r)的公式不同，P点的高斯曲率 K可以这样计算：

$K = \lim_{r \rarr 0} (2 \pi r - \mbox{C}(r)) \cdot \frac{3}{\pi r^3}.$

高斯曲率在整个曲面上的积分和曲面的欧拉示性数有密切关联；参见高斯-博内定理。

平均曲率等于主曲率的和，k₁+k₂，除以 2。其单位为1／长度。平均曲率和曲面面积的第一变分密切相关，特别的，像肥皂膜这样的最小曲面平均曲率为0，而肥皂泡平均曲率为常数。不像高斯曲率，平均曲率依赖于嵌入，例如，一个圆柱和一个平面是局部等距的，但是平面的平均曲率为0，而圆柱的非零。

空间的曲率

在宇宙学上，需要考虑"空间的曲率"，就是相应的伪黎曼流形的曲率，见黎曼流形的曲率。

没有曲率的空间成为平坦空间或欧几里得空间。另见宇宙的形状。

参考

• 曲率形式 包含对于有联络的向量丛和主丛的曲率的正确描述。
• 黎曼流形曲率 有高斯曲率在高维黎曼流形上的推广。
• 曲率向量和测地曲率 黎曼曲面上的曲线的曲率的描述。
• 高斯映射有高斯曲率的更多几何属性。
• 高斯-博内定理有曲率的基本应用