在数学中,双曲线(英語:hyperbola;希臘語:ὑπερβολή,意思是超过、超出)是定义为平面交截直角圆锥面的两半的一类圆锥曲线。
它还可以定义为与两个固定的点(称为焦点)的距离差是常数的点的轨迹。这个固定的距离差是 的两倍,这里的
的两倍,这里的 是从双曲线的中心到双曲线最近的分支的顶点的距离。
是从双曲线的中心到双曲线最近的分支的顶点的距离。 还称为双曲线的半实轴。焦点位于贯轴上,它们的中间点称为中心。
还称为双曲线的半实轴。焦点位于贯轴上,它们的中间点称为中心。
从代数上说,双曲线是在笛卡尔平面上由如下方程定义的曲线

使得 ,这裡的所有系数都是实数,并存在定义在双曲线上的点对
,这裡的所有系数都是实数,并存在定义在双曲线上的点对 的多于一个的解。
的多于一个的解。
在笛卡尔坐标平面上,两个互为倒数的变量的图像是双曲线。
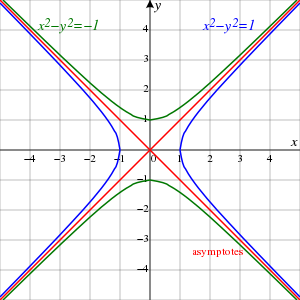 共轭单位直角双曲线
共轭单位直角双曲线
上面已经列出:
- 平面切直角圆锥面的两半的交截线。
- 与两个固定点(称为焦点)距离差为常数的点的轨迹。
- 到一个焦点的距离和到一条直线(称为准线)的距离的比例是大于
 的常数的点的轨迹。这个常数称为双曲线的离心率。
的常数的点的轨迹。这个常数称为双曲线的离心率。
双曲线由分开两个焦点的两个分离的称为臂或分支的曲线构成。随着到焦点的距离的变大,双曲线就越逼近称为渐近线的两条线。渐近线交叉于双曲线的中点,并对于东西开口的双曲线有斜率 ,对于北南开口的双曲线有斜率
,对于北南开口的双曲线有斜率 。
。
双曲线有个性質,出自一个焦点的射线反射于双曲线后看起来像是出自另一个焦点。
双曲线的一个特殊情况是“等轴”或“直角”双曲线,它的渐近线交于直角。以坐标轴作为渐近线的直角双曲线由方程 给出,这裡的
给出,这裡的 是常数。
是常数。
如果对双曲线方程交换 和
和 ,得到它的共轭双曲线。共轭双曲线有同样的渐近线。
,得到它的共轭双曲线。共轭双曲线有同样的渐近线。
笛卡尔坐标[编辑]
中心位于 的左右开口的双曲线:
的左右开口的双曲线:

中心位于 的上下开口的双曲线:
的上下开口的双曲线:

实轴贯穿双曲线的中心并交双曲线两臂于它们的顶点。焦点位于双曲线实轴的延长线上。虚轴贯穿双曲线中点并垂直于实轴。
在两个公式中, 是半实轴(在双曲线两臂之间沿着实轴测量的距离),而
是半实轴(在双曲线两臂之间沿着实轴测量的距离),而 是半虚轴。
是半虚轴。
如果用双曲线的两个顶点的切线交渐近线形成一个矩形,在切线上的两边的长度是 ,平行于实轴的两边的长度是
,平行于实轴的两边的长度是 ,注意
,注意 可以大于
可以大于 。
。
如果计算从双曲线上任意准线上的点到每个焦点的距离,这两个距离的差的绝对值总是 。
。
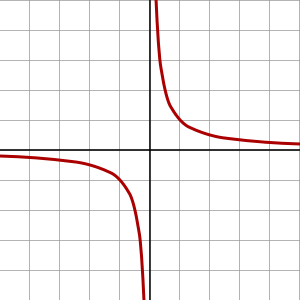 直角双曲线
直角双曲线 的图像。
的图像。
离心率给出自:

左右开口的双曲线的焦点是: ,其中c给出自
,其中c给出自 。
。
上下开口的双曲线的焦点是: ,其中c给出自
,其中c给出自 。
。
等軸雙曲線[编辑]
等轴双曲线的实轴与虚轴长相等,即 且
且 ,此时渐近线方程为
,此时渐近线方程为 (无论焦点在
(无论焦点在 轴还是
轴还是 轴)。
轴)。
单位双曲线属于等轴双曲线,且半实轴和半虚轴的长均为 ,即
,即 ,满足方程:
,满足方程:
 或
或 。
。
对于以直线 和直线
和直线 为渐近线的直角双曲线:
为渐近线的直角双曲线:

这种双曲线最简单的例子是:

共軛雙曲線[编辑]
當双曲线 的实轴是双曲线
的实轴是双曲线 的虚轴,且双曲线
的虚轴,且双曲线 的虚轴是双曲线
的虚轴是双曲线 的实轴时,称双曲线
的实轴时,称双曲线 与双曲线
与双曲线 为共轭双曲线。若
为共轭双曲线。若 的方程為
的方程為

則 的方程為
的方程為

其特点為:
- 共渐近线,与渐近线平行的直线和双曲线有且只有一个交点。
- 焦距相等。
- 两双曲线的离心率平方后的倒数相加等于
 。
。
极坐标[编辑]
左右开口的双曲线:

上下开口的双曲线:

上右下左开口的双曲线:

上左下右开口的双曲线:

在所有公式中,中心在极点,而 是半实轴和半虚轴。
是半实轴和半虚轴。
双曲线的参数方程[编辑]
如同正弦和余弦函数给出椭圆的参数方程,双曲函数给出双曲线的参数方程。
左右开口的双曲线:

或

上下开口的双曲线:

或

在所有公式中, 是双曲线的中点,
是双曲线的中点, 是半实轴而
是半实轴而 是半虚轴。
是半虚轴。
双曲线的标准方程[编辑]
焦点在 轴:
轴:
焦点在 轴:
轴:
双曲线的渐近线方程[编辑]
焦線平行於 轴:
轴:
焦線平行於 轴:
轴:
圆锥曲线方程[编辑]

当 时,表示双曲线。其中
时,表示双曲线。其中 为焦点到准线距离,
为焦点到准线距离, 为弦与
为弦与 轴夹角。
轴夹角。
参考文献[编辑]
外部链接[编辑]






















































