平行四边形

平行四边形
平行四边形
類型	四邊形
邊	4
頂點	4
對稱群	D1 (*)
面積	見下文
對偶	平行四边形(本身)

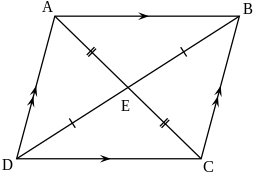
两组对边分别平行的四边形称为平行四边形。平行四边形一般用图形名称加依次四个顶点名称来表示，如图平行四边形记为平行四边形ABCD。

性质

1. 一组对边平行且相等
2. 两个对角大小相等
3. 相邻的两个角互补
4. 对角线互相平分
5. 兩雙對邊等長
6. 對於平面上任何一點，都存在一條能將平行四邊形平分為兩個面積相等圖形、並穿過該點的線。
7. 四邊邊長的平方和等於兩條對角線的平方和。

分类

矩形、菱形、正方形是特殊的平行四边形。

判定

意思就是, 只要符合其中一項性質的四邊形, 必定是平行四邊形 又稱「平行四邊形判別性質」

1. 两对对边平行
2. 一对对边平行且相等
3. 在同一平面内，对角线互相平分
4. 在同一平面内，两对对边相等
5. 在同一平面内，两对对角相等
6. 在同一平面内，一对对角相等且两对对边相等

面积

图中蓝色区域为平行四边形的面积

公式一：

$S = B \times H$

公式二：

$S = B \cdot C \cdot \sin \theta.\,$

公式三：

$K = \frac{|\tan \gamma|}{2} \cdot \left| B^2 - C^2 \right|.$

（其中γ是对角线夹角，B,C为两条邻边）

参见

• 平行四邊形恆等式
• 泰博定理
• 伐里農平行四邊形