 方程
方程 表示的例子椭球:
表示的例子椭球:
球面 (上图, a=b=c=4),
类球面 (下左, a=b=5, c=3),
三轴椭球面 (下右, a=4.5, b=6, c=3)
椭球是一种二次曲面,是椭圆在三维空间的推广。
标准方程[编辑]
椭球在xyz-笛卡儿坐标系中的方程式:

其中a和b是赤道半径(沿着x和y轴),c是极半径(沿着z轴)。这三个数都是固定的正实数,决定了椭球的形状。
如果三个半径都是相等的,那么就是一个球;如果有两个半径是相等的,则是一个类球面。
 :球;
:球; :扁球面(类似盤状);
:扁球面(类似盤状); :长球面(类似條状);
:长球面(类似條状); :不等边椭球(“三条边都不相等”)。
:不等边椭球(“三条边都不相等”)。
点(a,0,0)、(0,b,0)和(0,0,c)都在曲面上。从原点到这三个点的线段,称为椭球的半主轴。它们与椭圆的半长轴和半短轴相对应。
参数化[编辑]
使用球坐标系,其中 是天顶角,
是天顶角, 是方位角,则椭球可以表示为以下的参数形式:
是方位角,则椭球可以表示为以下的参数形式:


 以扁椭球的XZ截面为例,这里的高度角是t,目标点是P,t不是点P的大地纬度,也不是它的地心纬度,由于此参数定义而被阿瑟·凱萊称为“参数纬度”[1] 。
以扁椭球的XZ截面为例,这里的高度角是t,目标点是P,t不是点P的大地纬度,也不是它的地心纬度,由于此参数定义而被阿瑟·凱萊称为“参数纬度”[1] 。
使用地理坐标系,其中 是一点的参数纬度,
是一点的参数纬度, 是该点的经度:
是该点的经度:


- (注意,当
 时,也就是在极点时,这个参数不是一一对应的)
时,也就是在极点时,这个参数不是一一对应的)
体积和表面积[编辑]
椭球的体积由以下公式给出:

注意,当三个半径都相等时,这个公式便化为球的体积;两个半径相等时,便化为扁球面或长球面的体积。
表面积[编辑]
椭球的表面积由以下公式给出:
![{\displaystyle S=2\pi \left[c^{2}+b{\sqrt {a^{2}-c^{2}}}F\left(o\!\varepsilon ,{\frac {b^{2}-c^{2}}{b^{2}\sin ^{2}o\!\varepsilon }}\right)+{\frac {bc^{2}}{\sqrt {a^{2}-c^{2}}}}E\left(o\!\varepsilon ,{\frac {b^{2}-c^{2}}{b^{2}\sin ^{2}o\!\varepsilon }}\right)\right],\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/057bfba6c87d7954fb2ef38f13a906b32af9e88c)
其中
 (扁球面)或
(扁球面)或 (长球面),是角离心率;
(长球面),是角离心率; 、
、 是第一类和第二类不完全椭圆积分。
是第一类和第二类不完全椭圆积分。
与球的表面积不同,椭球的表面积一般不能用初等函数来表示。
一个近似公式为:

其中 。这样相对误差最多为
。这样相对误差最多为 %(Knud Thomsen公式);
%(Knud Thomsen公式); 的值对于接近于球的椭球较为适宜,其相对误差最多为
的值对于接近于球的椭球较为适宜,其相对误差最多为 %(David W. Cantrell公式)。
%(David W. Cantrell公式)。
对于 的情况,有一个精确的公式:
的情况,有一个精确的公式:
- 扁球面:

- 长球面:

 比
比 和
和 都小很多时,表面积近似等于
都小很多时,表面积近似等于 。
。
椭球与平面相交的横截面[编辑]
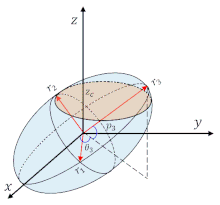 示意图:一个三轴椭球和平行于XY平面的水平平面相交。
示意图:一个三轴椭球和平行于XY平面的水平平面相交。
椭球与平面相交的横截面为椭圆。如右图所示,椭圆的两个直径  与
与  可表示为[2]
可表示为[2]

线性变换[编辑]
如果我们对球使用可逆的线性变换,便可以得到一个椭球;它可以用旋转的方法来化成以上标准的形式,这是谱定理的结果。如果该线性变换用一个对称的3乘3矩阵来表示的话,那么这个矩阵的特征向量就是正交的(根据谱定理),它表示了轴的方向:而半轴的长度则由特征值给出。
椭球与平面的交集是空集、一个点,或一个椭圆。
我们也可以利用经过线性变换的球来定义多维空间的椭球,并使用谱定理来得出一个标准方程。
质量性质[编辑]
均匀密度的椭球的质量为:

其中 是密度。
是密度。
均匀密度的椭球的转动惯量为:



其中 、
、 和
和 分别是关于x、y和z轴的转动惯量。惯性积为零。
分别是关于x、y和z轴的转动惯量。惯性积为零。
容易知道,如果a=b=c,那么上述公式便化为均匀密度的球的转动惯量。
反过来,如果知道了一个任意刚体的质量和主惯性矩,那么就可以构造出一个等价的均匀密度的椭球,使用以下特征:




鸡蛋形[编辑]
鸡蛋的形状可以近似地认为是半个长球面与半个球在赤道处相拼合而成,共用一个旋转对称的主轴。[3]虽然鸡蛋形通常意味着在赤道平面没有反射对称,它也可以用来指真正的长球面。它也可以用来描述相应的二维图形。参见鵝蛋形。
参考文献[编辑]
外部連結[编辑]



















![{\displaystyle S=2\pi \left[c^{2}+b{\sqrt {a^{2}-c^{2}}}F\left(o\!\varepsilon ,{\frac {b^{2}-c^{2}}{b^{2}\sin ^{2}o\!\varepsilon }}\right)+{\frac {bc^{2}}{\sqrt {a^{2}-c^{2}}}}E\left(o\!\varepsilon ,{\frac {b^{2}-c^{2}}{b^{2}\sin ^{2}o\!\varepsilon }}\right)\right],\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/057bfba6c87d7954fb2ef38f13a906b32af9e88c)






























