五边形
| 正五邊形 | |
|---|---|
 一個正五邊形 | |
| 類型 | 正多邊形 |
| 對偶 | 正五邊形(本身) |
| 邊 | 5 |
| 頂點 | 5 |
| 對角線 | 5 |
| 施萊夫利符號 | {5} |
| 考克斯特符號 | |
| 對稱群 | 二面體群 (D5), order 2×5 |
| 面積 | |
| 內角(度) | 108° |
| 內角和 | 540° |
| 特性 | 凸、圓內接多邊形、等邊多邊形、等角多邊形、等邊圖形 |
在幾何學中,五邊形是指有五條邊和五個頂點的多邊形,其內角和為540度。
五邊形可以分為凸五邊形和非凸五邊形,其中非凸五邊形包含了凹五邊形和另一種邊自我相交的五角星。最簡單的五角星可藉由將正五邊形的對角線連起來構成。
正五邊形[编辑]
正五邊形是指五個邊等長且五個角等角的五邊形,其內角為108度,是一種正多邊形,在施萊夫利符號中可以用來表示。
正五邊形的中心角為72度,其具有五個對稱軸,其旋轉對稱性有5個階(72°、144°、216° 和 288°)。
- 高邊長邊長
- 寬邊長邊長
- 對角線長
邊長為的正凸五邊形面積可以將之分割成5個等腰三角形計算:
正五邊形不能鑲嵌平面,因為其內角是108°,不能整除360°。截至2015年[update],2017年5月,里昂高等师范学校Michaël Rao宣称已证明只存在15种凸五边形鑲嵌平面情况。[1]。
面積公式推導[编辑]
其中,是正五邊形的邊長。
內切圓半徑[编辑]
正五邊形是一個圓外切多邊形,因此有內切圓。其內切圓半徑與邊心距相同,並且可以尤其邊長來決定。
其中,為內切圓半徑與邊心距相同、t為正五邊形邊長。
構造[编辑]

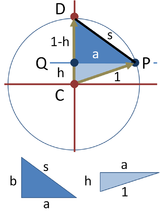
里士滿提出了一個構造正五邊形的方法[2],並且在克倫威爾的《多面體》中被進一步討論。[3]。
右上的圖顯示了里士滿繪製正五邊形的方法。先利用單位圓決定五邊形的半徑。為單位圓圓心,是圓半徑的中點。是位於垂直於的另外一條半徑的圓周上。作的角平分線,令為的角平分線與的交點。作過平行於的直線,令之與圓相交的交點為,則為正五邊形的邊長。
這條邊的長度可以利用圓下方的兩個直角三角形和。利用勾股定理,較大的三角形斜邊為。小三角形其中一股h可由半角公式求得:
其中,角可由大三角形求得,其值為:
由此可得到在下圖正五邊形的邊長的一些相關值。右側三角形的邊長可藉由再帶一次勾股定理得:
欲求出五邊形邊長可透過左側的三角形,由勾股定理得:

五邊形邊長為:
得到了正確的結果[4]因此此種構造正五邊形的方法是有效的。
約西元前300年,欧几里得在他的《几何原本》中描述了一个用直尺和圆规做出正五边形的过程。
物理方法[编辑]

正五邊形可以藉由嘗試在一張長條紙張上打一個反手結,並將多出來的部分向後折來構造。這種折法被用在摺紙星星上。
等邊五邊形[编辑]

等邊五邊形是指五條邊等長的五邊形。等邊五邊形不一定是正五邊形。由於其內角可以取自一個範圍內的集合,而形成一個等邊五邊形的群,相比之下,正五邊形由於其內角也固定了,因此是唯一的。
有兩個直角的等邊五邊形由於外形與有屋頂的房屋形狀非常相似,因此通常用作房子的符號。
五邊形鑲嵌[编辑]
五邊形鑲嵌是指用全等的五邊形沒有空隙地填滿整個平面的鑲嵌圖形。2017年5月,里昂高等师范学校Michaël Rao宣称已证明只存在15种凸五边形鑲嵌平面情况[1]。

扭歪五邊形[编辑]
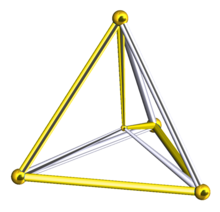
扭歪五邊形,又稱不共面五邊形,是指頂點並非完全共面的五邊形。
皮特里多邊形[编辑]
一些高維度多胞體的皮特里多邊形是扭歪五邊形,例如四維正五胞體[5]。
類五邊形形[编辑]
類五邊形形是五邊形在其他維度的類比,只存在於四維或以下的空間。這些形狀都具有Hn的考克斯特群[6][7][8],其中正五邊形為H2,階數為10。
| 維度 | 二維 | 三維 | 四維 |
|---|---|---|---|
| 類五邊形形 | 
|

|

|
| 對偶 | 
|

|

|
由五邊形組成的多面體[编辑]
有一些多面體由五邊形構成,最常見的就是正十二面體,是一個由正五邊形組成的正多面體。
| Ih | Th | Td | O | I | D5d |
|---|---|---|---|---|---|

|

|

|

|

|

|
| 正十二面體 | 黃鐵礦形五角十二面體 | 五角三四面體 | 五角二十四面體 | 五角六十面體 | 截對角五方偏方面體 |
参考文献[编辑]
- ^ 1.0 1.1 Exhaustive search of convex pentagons which tile the plane (PDF). [2019-07-29]. (原始内容存档 (PDF)于2020-11-12).
- ^ Herbert W Richmond. Pentagon. 1893 [2016-08-28]. (原始内容存档于2020-11-27).
- ^ Peter R. Cromwell. Polyhedra. : 63 [2016-08-28]. ISBN 0-521-66405-5. (原始内容存档于2020-10-03).
- ^ This result agrees with Herbert Edwin Hawkes; William Arthur Luby; Frank Charles Touton. Exercise 175. Plane geometry. Ginn & Co. 1920: 302 [2016-08-28]. (原始内容存档于2014-01-01).
- ^ H.S.M. Coxeter Regular Polytopes, 3rd edition, 1973
- ^ Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (页面存档备份,存于互联网档案馆)
- ^ (Paper 10) H.S.M. Coxeter, Star Polytopes and the Schlafli Function f(α,β,γ) [Elemente der Mathematik 44 (2) (1989) 25–36]
- ^ Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Table I(ii): 16 regular polytopes {p, q, r} in four dimensions, pp. 292–293)
参见[编辑]
| ||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




































