 椭圆和它的某些数学性质
椭圆和它的某些数学性质
在数学中,椭圆是平面上到两个相異固定点的距离之和为常数的点之轨迹。
根據該定義,可以用手繪橢圓:先準備一條線,將這條線的兩端各綁在固定的點上(這兩個點就當作是橢圓的兩個焦點,且距離小於線長);取一支筆,用筆尖将線繃緊,這時候兩個點和筆就形成一個三角形(的兩邊);然後左右移動筆尖拉住線開始作圖,持續地使線繃緊,最後就可以完成一個橢圓圖形。
由於兩個固定點之間的距離也是一定的,所以可以省去綁在點上這一步驟而改將線綁成環狀,然後以筆尖和這兩個焦點將線繃直即可。下同。
 一個平面切截一個圓錐面得到的橢圓。
一個平面切截一個圓錐面得到的橢圓。
椭圆是一种圆锥曲线:如果一个平面切截一个圆锥面,且不与它的底面相交,也不与它的底面平行,则圆锥和平面交截线是个椭圆。
在代数上说,椭圆是在笛卡尔平面上如下形式的方程所定义的曲线

使得  ,这里的係数都是实数,并存在定义在椭圆上的点对 (x, y) 的多于一个的解。
,这里的係数都是实数,并存在定义在椭圆上的点对 (x, y) 的多于一个的解。
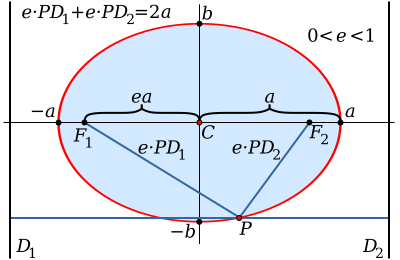
穿过两焦点并终止于椭圆上的线段AB叫做长轴。长轴是通过连接椭圆上的两个点所能获得的最长线段。穿过中心(两焦点的连线的中点)垂直于长轴并且终止于椭圆的线段CD叫做短轴。半長軸(图中指示为 a)是长轴的一半:从中心通过一个焦点到椭圆的边缘的线段。半短軸(图中指示为 b)是短轴的一半。
如果两个焦点重合,则这个椭圆是圆;换句话说,圆是离心率为零的椭圆。
中心位于原点的椭圆  可以被看作单位圆在关联于对称矩阵
可以被看作单位圆在关联于对称矩阵  的线性映射下的图像,这里的 D 是带有
的线性映射下的图像,这里的 D 是带有  的特征值的对角矩阵,二者沿着主对角线都是正实数的,而 P 是拥有
的特征值的对角矩阵,二者沿着主对角线都是正实数的,而 P 是拥有  的特征向量作为纵列的实数的酉矩阵。椭圆的长短轴分别沿着
的特征向量作为纵列的实数的酉矩阵。椭圆的长短轴分别沿着  的两个特征向量的方向,而两个与之对应的特征值分别是半长轴和半短轴的长度的平方的倒数。
的两个特征向量的方向,而两个与之对应的特征值分别是半长轴和半短轴的长度的平方的倒数。
椭圆可以通过对一个圆的所有点的 x 坐标乘以一个常数而不改变 y 坐标来生成。
离心率[编辑]
 形狀母數:
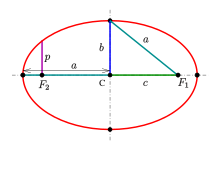
形狀母數:- C:中心
- F1:焦點一;
- F2:焦點二;
- a:半长轴;
- b:半短轴;
- c:半焦距;
- p:半正焦弦(通常標示作
 )。
)。
椭圆的形状可以用叫做椭圆的离心率的一个数来表达,习惯上指示为  。离心率是小于 1 大于等于 0 的实数。离心率 0 表示着两个焦点重合而这个椭圆是圆。
。离心率是小于 1 大于等于 0 的实数。离心率 0 表示着两个焦点重合而这个椭圆是圆。
对于有半长轴 a 和半短轴 b 的椭圆,离心率是

离心率越大,a 与 b 的比率就越大,因此椭圆被更加拉长。
半焦距c 等于从中心到任一焦点的距离,

则

半焦距 c 也叫做椭圆的线性离心率。在两个焦点间的距离是 2c = 2aε。
 在正規位置上的橢圓的參數方程。參數 t 是藍線對於 X-軸的角度。
在正規位置上的橢圓的參數方程。參數 t 是藍線對於 X-軸的角度。
中心位于点  的主轴平行于 x 轴的椭圆由如下方程指定
的主轴平行于 x 轴的椭圆由如下方程指定

这个椭圆可以参数化表达为


这里的  可以限制于区间
可以限制于区间  。
。
如果  且
且  (就是说,如果中心是原点(0,0)),则
(就是说,如果中心是原点(0,0)),则


这个参数方程揭示了两个方向相互垂直的简谐运动(表现为具有周期性的简谐波)合成了闭合的椭圆形周期性运动(表现为轨迹是椭圆)。
| 椭圆方程
|

|

|
| 图像
|
|
|
| 范围
|

|

|
相對於中心的極坐標形式[编辑]
用极坐标可表达为

这里的  是椭圆的离心率;
是椭圆的离心率; 是
是  与
与  的夹角
的夹角
相對於焦點的極坐標形式[编辑]
 橢圓的極坐標,原點在 F1
橢圓的極坐標,原點在 F1
有一个焦点在原点的椭圆的极坐标方程是

这里的  是
是  与
与  的夹角
的夹角
半正焦弦和极坐标[编辑]
椭圆的半正焦弦(通常指示为  ),是从椭圆的一个焦点到椭圆自身,沿着垂直主轴的直线测量的距离。它有关于
),是从椭圆的一个焦点到椭圆自身,沿着垂直主轴的直线测量的距离。它有关于  和
和  (椭圆的半轴),通过公式
(椭圆的半轴),通过公式  或者如果使用离心率的话
或者如果使用离心率的话  。
。
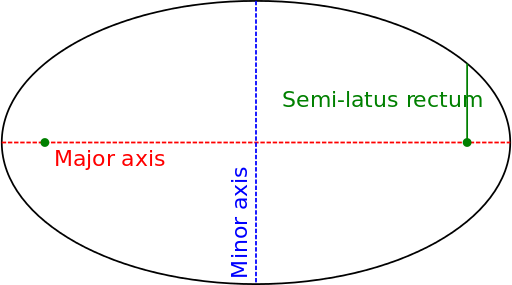 椭圆,使用半正焦弦展示
椭圆,使用半正焦弦展示
在极坐标中,一个焦点在原点而另一个焦点在负 x 轴上的椭圆给出自方程

椭圆可以被看作是圆的投影:在与水平面有角度 φ 的平面上的圆垂直投影到水平面上给出离心率 sin φ 的椭圆,假定 φ 不是 90°。
 橢圓(用紅色繪制)可以表達為内旋轮线在 R=2r 時的特殊情況。
橢圓(用紅色繪制)可以表達為内旋轮线在 R=2r 時的特殊情況。
面积和周长[编辑]
椭圆所包围的面积是  ,这里的
,这里的  ,和
,和 ,
是半长轴和半短轴。在圆的情况下
,
是半长轴和半短轴。在圆的情况下 ,表达式简化为
,表达式简化为  。
。
椭圆的周长是  ,这里的函数
,这里的函数 是第二类完全椭圆积分。
是第二类完全椭圆积分。
周长为: 或者
或者
精确的无穷级数为:
![{\displaystyle C=2\pi a\left[{1-\left({1 \over 2}\right)^{2}{\frac {c^{2}}{a^{2}}}-\left({1\cdot 3 \over 2\cdot 4}\right)^{2}{c^{4} \over {3a^{4}}}-\left({1\cdot 3\cdot 5 \over 2\cdot 4\cdot 6}\right)^{2}{c^{6} \over {5a^{6}}}-\dots }\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dfada5024276d3f82d18f849a5b95fb332eaacb)
或:
![{\displaystyle C=-2\pi a\sum _{n=0}^{\infty }{\left\lbrace \left[\prod _{m=1}^{n}\left({2m-1 \over 2m}\right)\right]^{2}{c^{2n} \over {{a^{2n}}\left(2n-1\right)}}\right\rbrace }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a57534cbe1f8f5c5b5fb48f3be75f7b37ec9f5ae)
拉马努金给出一较为接近的式子:
![{\displaystyle C\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd246503ae5e29912d4149f118c5d7145d637085)
它还可以写为:
![{\displaystyle C\approx 3a\pi \left[1+{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]-a\pi {\sqrt {\left[3+{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]\left[1+3{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]}}\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ad92a27ab7667d10fcdd89db63ed66ba331cc1)
还有一条近似很高的公式:
![{\displaystyle C\approx \pi (a+b)\left[1+{\frac {3\left({\frac {a-b}{a+b}}\right)^{2}}{10+{\sqrt {4-3\left({\frac {a-b}{a+b}}\right)^{2}}}}}\right]\left[1+\left({\frac {22}{7\pi }}-1\right)\left({\frac {a-b}{a}}\right)^{33}{\sqrt[{1000}]{\left({\frac {a-b}{a}}\right)^{697}}}\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62aa6152db65a0903657774d16c0477e7ea273d6)
标准方程的推导[编辑]
- 如果在一个平面内一个动点到两个定点的距离的和等于定长,那么这个动点的轨迹叫做椭圆。
假设(注意所有假设只是为了导出椭圆方程时比较简便)动点为 ,两个定点为
,两个定点为 和
和 ,则根据定义,动点
,则根据定义,动点 的轨迹方程满足(定义式):
的轨迹方程满足(定义式):
 ,其中
,其中 为定长。
为定长。
用两点的距离公式可得: ,
, ,代入定义式中,得:
,代入定义式中,得:
 ①
①
上式左方分子凑出平方差,并化简,得:
![{\displaystyle {\frac {\left(x+c\right)^{2}+y^{2}-\left[\left(x-c\right)^{2}+y^{2}\right]}{{\sqrt {\left(x+c\right)^{2}+y^{2}}}-{\sqrt {\left(x-c\right)^{2}+y^{2}}}}}=2a\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc56759682756dfdc31a8718c98b6a251963920d)
分子大部分相消,分母移项即得
 ②
②
①、②式相加并平方,整理得

当 时,并设
时,并设 ,则上式可以进一步化简:
,则上式可以进一步化简:

因为 ,将上式两边同除以
,将上式两边同除以 ,可得:
,可得:

则该方程即动点 的轨迹方程,即椭圆的方程。这个形式也是椭圆的标准方程。
的轨迹方程,即椭圆的方程。这个形式也是椭圆的标准方程。
- 椭圆的图像如果在直角坐标系中表示,那么上述定义中两个定点被定义在了x轴。若将两个定点改在y轴,可以用相同方法求出另一个椭圆的标准方程:

- 在方程中,所设的
 称为长轴长,
称为长轴长, 称为短轴长,而所设的定点称为焦点,那么
称为短轴长,而所设的定点称为焦点,那么 称为焦距。在假设的过程中,假设了
称为焦距。在假设的过程中,假设了 ,如果不这样假设,会发现得不到椭圆。当
,如果不这样假设,会发现得不到椭圆。当 时,这个动点的轨迹是一个线段;当
时,这个动点的轨迹是一个线段;当 时,根本得不到实际存在的轨迹,而这时,其轨迹称为虚椭圆。另外还要注意,在假设中,还有一处:
时,根本得不到实际存在的轨迹,而这时,其轨迹称为虚椭圆。另外还要注意,在假设中,还有一处: 。
。
- 通常认为圆是椭圆的一种特殊情况。
椭圆的旋转和平移[编辑]
对于平面上任意椭圆  ,总可以将之转化为
,总可以将之转化为

的形式。具体步骤为,将后式的各乘积乘方项展开,根据与前式对应项係数相等的法则便可求得u,v,f的值。其中, 便是该椭圆的中心(f=0)。
便是该椭圆的中心(f=0)。
若将


代入式中便可得到平移前的椭圆。
若 ,则表示椭圆的长短轴与坐标系的坐标轴并不平行或垂直,即发生了旋转。设旋转的角度为
,则表示椭圆的长短轴与坐标系的坐标轴并不平行或垂直,即发生了旋转。设旋转的角度为 ,则有
,则有

当 ,则说明
,则说明 。
。
若将


代入式中便可得到旋转前的椭圆。
漸開線及其導數[编辑]

![{\displaystyle {\begin{cases}{\cfrac {{\rm {d}}x}{\rm {{d}t}}}={\cfrac {\left[b^{2}\sin 2t-2b^{2}\sin t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\right]\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right)-ab\left(a^{2}-b^{2}\right)\sin 2t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\sin t}{2\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right){\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}}}-a\sin t\!\,\\\\{\cfrac {{\rm {d}}y}{\rm {{d}t}}}={\cfrac {\left[b^{3}\sin 2t-2ab^{2}\sin t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\right]\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right)-ab^{2}\left(a^{2}-b^{2}\right)\sin 2t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\sin t}{2a\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right){\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}}}+b\cos t\!\,\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fb25c21dda4b86817dbaf019bd92ed03bb4bd94)
有了橢圓漸開線的導數,可以計算它的長度,其中 是第二類完全橢圓積分。
是第二類完全橢圓積分。
外部链接[编辑]
























































![{\displaystyle C=2\pi a\left[{1-\left({1 \over 2}\right)^{2}{\frac {c^{2}}{a^{2}}}-\left({1\cdot 3 \over 2\cdot 4}\right)^{2}{c^{4} \over {3a^{4}}}-\left({1\cdot 3\cdot 5 \over 2\cdot 4\cdot 6}\right)^{2}{c^{6} \over {5a^{6}}}-\dots }\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dfada5024276d3f82d18f849a5b95fb332eaacb)
![{\displaystyle C=-2\pi a\sum _{n=0}^{\infty }{\left\lbrace \left[\prod _{m=1}^{n}\left({2m-1 \over 2m}\right)\right]^{2}{c^{2n} \over {{a^{2n}}\left(2n-1\right)}}\right\rbrace }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a57534cbe1f8f5c5b5fb48f3be75f7b37ec9f5ae)
![{\displaystyle C\approx \pi \left[3(a+b)-{\sqrt {(3a+b)(a+3b)}}\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd246503ae5e29912d4149f118c5d7145d637085)
![{\displaystyle C\approx 3a\pi \left[1+{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]-a\pi {\sqrt {\left[3+{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]\left[1+3{\sqrt {1-\left({\frac {c}{a}}\right)^{2}}}\right]}}\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ad92a27ab7667d10fcdd89db63ed66ba331cc1)
![{\displaystyle C\approx \pi (a+b)\left[1+{\frac {3\left({\frac {a-b}{a+b}}\right)^{2}}{10+{\sqrt {4-3\left({\frac {a-b}{a+b}}\right)^{2}}}}}\right]\left[1+\left({\frac {22}{7\pi }}-1\right)\left({\frac {a-b}{a}}\right)^{33}{\sqrt[{1000}]{\left({\frac {a-b}{a}}\right)^{697}}}\right]\!\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62aa6152db65a0903657774d16c0477e7ea273d6)









![{\displaystyle {\frac {\left(x+c\right)^{2}+y^{2}-\left[\left(x-c\right)^{2}+y^{2}\right]}{{\sqrt {\left(x+c\right)^{2}+y^{2}}}-{\sqrt {\left(x-c\right)^{2}+y^{2}}}}}=2a\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc56759682756dfdc31a8718c98b6a251963920d)


























![{\displaystyle {\begin{cases}{\cfrac {{\rm {d}}x}{\rm {{d}t}}}={\cfrac {\left[b^{2}\sin 2t-2b^{2}\sin t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\right]\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right)-ab\left(a^{2}-b^{2}\right)\sin 2t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\sin t}{2\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right){\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}}}-a\sin t\!\,\\\\{\cfrac {{\rm {d}}y}{\rm {{d}t}}}={\cfrac {\left[b^{3}\sin 2t-2ab^{2}\sin t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\right]\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right)-ab^{2}\left(a^{2}-b^{2}\right)\sin 2t\cdot E\left(t,{\cfrac {\sqrt {a^{2}-b^{2}}}{a}}\right)\sin t}{2a\left(a^{2}\sin ^{2}t+b^{2}\cos ^{2}t\right){\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}}}+b\cos t\!\,\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fb25c21dda4b86817dbaf019bd92ed03bb4bd94)
