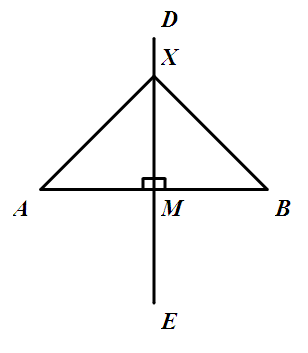
垂直平分線

垂直平分線,或稱中垂線,指一垂直於某個線段且經過該線段中點之直線。两个成轴对称的点连成的线段被其对称轴垂直平分。中垂線亦可成為平角的角平分線。
尺規作圖[编辑]
分別以該線段兩端點為圓心,大於線段一半之等長長度為半徑畫弧,兩弧相交之兩點連接成的直線即為該線段的垂直平分線。
垂直平分線性質[编辑]
垂直平分線上任一點到線段兩端點等距。 若直線L為之垂直平分線,則直線L上任意一點P可以使線段
垂直平分线上任一点与线段两端点相连构成的角被垂直平分线所平分。 直线L平分。
證明[编辑]
在和中:
(定義),
(定義),
(公共邊)
, 且
(Q.E.D.)
外心[编辑]
任意三角形ABC中,AB、AC、BC中垂線交於一點O,則我們稱此點O為三角形ABC的外心。
鈍角三角形的外心恆在圖形外部,直角三角形的外心恆在斜邊中點,銳角三角形的外心恆在圖形內部。
參見[编辑]
外部链接[编辑]
- The Angle Bisector(页面存档备份,存于互联网档案馆) at cut-the-knot
- Angle Bisector definition. Math Open Reference(页面存档备份,存于互联网档案馆) With interactive applet
- Line Bisector definition. Math Open Reference(页面存档备份,存于互联网档案馆) With interactive applet
- Perpendicular Line Bisector.(页面存档备份,存于互联网档案馆) With interactive applet
- Animated instructions for bisecting an angle(页面存档备份,存于互联网档案馆) and bisecting a line(页面存档备份,存于互联网档案馆) Using a compass and straightedge
- 埃里克·韦斯坦因. Line Bisector. MathWorld.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||