圆台
| 此條目没有列出任何参考或来源。 (2022年12月4日) |
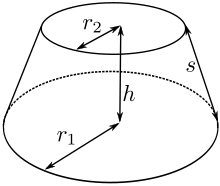

圓台,又稱截頂圓錐、圓亭,是几何学中研究的一类三维形体,指一个圆锥被平行于它的底面的一个平面所截後,截面与底面之间的几何形体。截面也称为圆台的上底面,原来圆锥的底面称为下底面。随着圆锥形状不同,圆台的称呼也不相同。一般说到圆台都是指正圆台,也就是指正圆锥截出的圆台。正圆台和圆形有相同的对称结构。以下除非另作注明,“圆台”都指正圆台。
性质[编辑]
体积[编辑]
圆台的体积取决于两底面之间的距离(圆台的高),以及原来圆锥的体积。设為圆台的高,和為棱台的上下底面半径, 為圆台的体积。由于圆台是由一个平面截去圆锥的一部分(也就是和原来圆锥相似的一个小圆锥)得到,所以计算体积的时候,可以先算出原来圆锥的体积,再减去和它相似的小圆锥的体积。圆锥被平行于底面的平面所截时,截面圆的半径与底面半径的比,等于小圆锥和原圆锥的高的比。假设原圆锥的高是,那么小圆锥的高是。也就是说:
所以:
圆台的体积等于原圆锥体积减去小圆锥的体积:
《九章算術》記載的圓台體積公式:「上下周相乘,又各自乘,并之,以高乘之,三十六而一。」这是将圆周率的值取为3得到的。
表面积[编辑]
圆台的侧面展开图是一个“扇面形”,也就是两个同心扇形的差。展开图的面积,就是两个扇形的面积差,其中是圆台的母线长度:
圆台的表面积St等于圆台的侧面积Sc加上两底的面积Su、Sd。
参看[编辑]
参考资料[编辑]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












![{\displaystyle S_{t}=S_{c}+S_{u}+S_{d}=\pi \left[R^{2}+r^{2}+(R+r)l\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79f390488b5e6eabf508d472b46e61767c4458dd)