加法器
在电子学中,加法器(英語:adder)是一种用于执行加法运算的数位电路部件,是构成电子计算机核心微处理器中算术逻辑单元的基础。在这些电子系统中,加法器主要负责计算地址、索引等数据。除此之外,加法器也是其他一些硬件,例如二进制数的乘法器的重要组成部分。
尽管可以为不同计数系统设计专门的加法器,但是由于数位电路通常以二进制为基础,因此二进制加法器在实际应用中最为普遍。在数字电路中,二进制数的减法可以通过加一个负数来间接完成。为了使负数的计算能够直接用加法器来完成,计算中的负数可以使用二补数(补码)来表示,具体的细节可以参考数位电路相关的书籍。[1]:244-248
半加器[编辑]
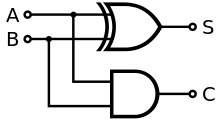
(英語:half adder)的功能是将两个一位二进制数相加。它有两个输出:
- 和:记作 S,来自对应的英语 Sum;
- 进位:记作 C,来自对应的英语 Carry一位的数字。因此,这两个一位二进制数的和用十进制表示即等于2C + S。右图是一个最简单的半加器设计,使用一个异或门来产生 S,一个与门来产生 C。和 S 的布尔逻辑是 A'B+AB',进位 C 的布尔逻辑是 AB。如果再添加一个或门处理两个半加器的进位信号,就构成了一个全加器。
半加器将两个输入位加和,产生进位与和,是半加器的两个输出。半加器的输入变量叫做被加数或被加位。输出变量为和与进位。
半加器的真值表如下:
| 输入 | 输出 | ||
|---|---|---|---|
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
全加器[编辑]

全加器(full adder)将两个一位二进制数相加,并根据接收到的低位进位信号,输出和、进位输出。全加器的三个输入信号为两个加数A、B和低位进位Cin。[3]全加器通常可以通过级联(cascade)的方式,构成多位(如8位、16位、32位)二进制数加法器的基本部分。全加器的输出和半加器类似,包括向高位的进位信号Cout和本位的和信号S,相加结果的总和用十進位表达为。一位全加器的真值表为:
| 输入 | 输出 | |||
|---|---|---|---|---|
| A | B | Cin | Cout | S |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
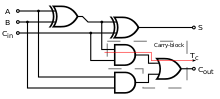
在实际的应用中,全加器可以通过不同的方式制造,例如直接利用晶体管级的电路,或者由其他现成的逻辑门来构成。和、进位信号对应的逻辑函数表达式分别为以及。另一种全加器电路与之前的方式略有不同,它用一个异或门来代替或门对其中两个输入信号进行求和,其进位信号对应的逻辑函数表达式分别为。通过适当的逻辑函数变化,可以证明它与前面的计算方法结果一致。[1]:238, 260
在这个实现中,将最后的或门换成异或门不会影响逻辑。如果电路使用的是每个芯片上只有一种閘的简单集成电路芯片,仅使用两种閘会比较方便。
全加器可以用两个半加器来构造,将输入端A和B连接到一个半加器上,然后将其和输出信号与进位输入信号分别作为第二个半加器的两个输入,并将两个进位输出信号进行逻辑或运算。全加器的关键路径(critical path,即经历最多逻辑门的路径)经过两个异或门,终止于和位 。假定异或门耗费3个延迟来完成,一个全加器的关键路径上施加的延迟等于
进位模块(carry-block)包括2个逻辑门,因此延迟为
全加器还可以使用一个三输入的异或门来求和,再使用一个两级与或结构来实现进位信号对应的积之和(sum of products)式。
多位加法器[编辑]
波纹进位加法器(脉动进位加法器)[编辑]
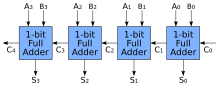
可以使用多个一位全加器来构成N位加法器,其中对应低位的全加器将其进位输出信号Cout连接到高一位的全加器的进入输入端Cin。这种构成多位加法器的形式被称为“波纹进位加法器”或“脉动进位加法器”(ripple-carry adder),“波纹”形象地描述了进位信号依次向前传递的情形。如果不需要连接其他进位信号,则最低位的全加器可以用半加器替换。
波纹進位加法器的电路布局形式较为简单,设计这种电路花费时间较短。然而,波纹进位加法器的进位输出、输入所经过的路径上比其他布局方式具有较多的邏輯閘,高位的计算必须等待低位的进位输出信号被计算出来才能开始,因此造成了更大的延迟时间。[4]:49
下面简单计算信号在加法器中的延迟。每一个全加器具有三级逻辑函数。在一个32位的波纹进位加法器中,有32个全加器,随之产生的邏輯閘延迟则可以根据关键路径的延迟时间来决定,即2倍的最高位全加器输入信号、进位输出延迟,加上31乘以3倍的其他全加器上的延迟,总共等于95倍的邏輯閘延迟。一个 n 位波纹進位加法器的最坏情形延迟方程为
从位位置0到进位输出的进位有一点不同:
交替进位极性和优化的与或非门的设计可以减少一半的延迟时间。[5]
超前进位加法器[编辑]
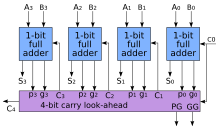
为了减少多位二进制数加减计算所需的时间,工程师设计了一种比脉动进位加法器速度更快的加法器电路,这种加法器被称为“超前进位加法器”(carry-lookahead adder)。
下面简述超前进位加法器的主要原理。[6][1]:255-262我们先来考虑构成多位加法器的单个全加器从其低一位获得的进位信号,我们可以将它变换为。现在为二进制数的每一位构建两个新信号:
于是,某位全加器从低一位获得的进位可以表示为,例如次低位全加器从最低位获得的进位为,而从最低位开始第三位的那个全加器获得的进位信号则为。在多位脉动进位加法器中,必须连接到低一位的进位输出信号,如果使用这种方式构成多位全加器,则逻辑门的延迟会发生累加,导致降低电路的计算效率下降。超前进位加法器采取的方式是,将的逻辑函数代入到,即,于是,这一位的进位输出就只取决于、、、、几个信号,而这几个信号都是计算电路外部的已知信号,而非低一位的计算结果。上面考虑的是从最低位开始第三位的情况。采用类似的代入方法,可以用各位的生成信号、传输信号,以及最低位从外部获取的进位信号来表示多位全加器的所有进位信号。

通过列出多位加法器各位的进位输出,可以发现高位的进位输出表达式(积之和式)涉及的变量更多,对应的逻辑电路连线会变得更复杂,而且在实际应用中会遭遇逻辑门的扇入问题。因此有必要对位数过高的全加器进行逻辑划分,如将六十四位全加器分为四个十六位超前进位加法器来实现(如右图)。多位二进制数加法器的标准芯片通常具有超前进位的组成形式,例如:7400系列的7483、74283芯片。[4]:50
延伸[编辑]
参考文献[编辑]
- ^ 1.0 1.1 1.2 Stephen Brown, Zvonko Vranesic. Fundamentals of Digital Logic with Verilog Design. McGraw-Hill Education. 2002. ISBN 0-07-283878-7.
- ^ Geoffrey A. Lancaster. Excel HSC Software Design and Development. Pascal Press. 2004: 180 [2013-02-24]. ISBN 9781741251753. (原始内容存档于2013-12-31).
- ^ M. Morris Mano. Digital Logic and Computer Design. Prentice-Hall. 1979: 119-123. ISBN 0-13-214510-3.
- ^ 4.0 4.1 邓元庆,关宇,贾鹏,石会. 数字设计基础与应用. 清华大学出版社. ISBN 978-7-302-21406-9.
- ^ Burgess, N. Fast Ripple-Carry Adders in Standard-Cell CMOS VLSI (PDF). 20th IEEE Symposium on Computer Arithmetic. 2011: 103–111.
- ^ Fast Addition: Carry Lookahead Adders. University of Maryland. [2013-02-28]. (原始内容存档于2013-03-04).
外部链接[编辑]
- Hardware algorithms for arithmetic modules(页面存档备份,存于互联网档案馆), includes description of several adder layouts with figures.
- 8-bit Full Adder and Subtractor(页面存档备份,存于互联网档案馆), a demonstration of an interactive Full Adder built in JavaScript solely for learning purposes.
| |||||||||||||||||









![{\displaystyle T_{CRA_{[0:c_{out}]}}=T_{HA}+n\cdot T_{c}=3D+n\cdot 2D}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aed8177ceb31f424ab84d3a142df2f1edb9b72b1)
![{\displaystyle T_{CRA_{[c_{0}:c_{n}]}}(n)=n\cdot T_{c}=n\cdot 2D}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bae801999e779eaa5b1e2b58ddff3c734b4ab362)
















