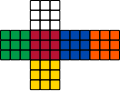
魔方
| 此條目的引用需要清理,使其符合格式。 (2014年5月22日) |
 魔方原状 | |
 打亂未還原且转动的魔方 | |
| 发明者 | 匈牙利建筑学教授暨雕塑家鲁比克·艾尔内 |
|---|---|
| 类型 | 机械益智玩具 |
| 分类 | |
| 正阶魔方 | 二阶魔方至33阶魔方 |
| 异形魔方 | 改造的正阶魔方,多轴魔方,电子魔方,魔板,魔表等 |
魔方,在台湾称为魔术方块,在香港和澳门称为扭计骰,為由匈牙利建築學教授暨雕塑家魯比克·艾爾內(Rubik Ernő)於1974年發明的機械益智玩具[1],最初的名稱叫Magic Cube[2],1980年Ideal Toys公司於販售此玩具,並將名稱改為Rubik's Cube[3]。
魔方在1980年代最為风靡,至今未衰,每年都會舉辦大小賽事。截至2009年1月,魔方在全世界售出了3億5千多萬個[4][5]。面世不久後,很多類似的玩具也紛紛出現,包括但不限于二階、四階、五階、六階、七階、八階、九階和十一階版本的魔方及其他变种。
魔術方塊的歷史[编辑]
早期的嘗試[编辑]
1970年3月,Larry Nichols發明了「Puzzle with Pieces Rotatable in Groups」,並申請了加拿大專利,是個2×2×2的魔術方塊,但是每個方塊之間是用磁鐵互相吸在一起。1972年獲得美國專利第3,655,201号,比魯比克教授的魔方早兩年。
第一個魔術方塊[编辑]
-
1980年,魔術方塊套裝,在匈牙利Ideal Toys公司製造的玩具。
-
魔術方塊的色塊
魯比克·厄爾諾是匈牙利的建築學和雕塑學教授,為了幫助學生們認識空間立方體的組成和結構,所以他自己動手做出了第一個魔方的雛形來,其靈感是來自於多瑙河中的沙礫[6]。
1974年,魯比克教授發明了第一個魔術方塊(當時稱作Magic Cube),並在1975年獲得匈牙利專利號HU170062,但沒有申請國際專利。第一批魔術方塊於1977年在布達佩斯的玩具店販售[7]。與Nichols的魔方不同,魯比克教授的零件是像卡榫一般互相咬合在一起,不容易因為外力而分開,而且可以以任何材質製作。
1979年9月,Ideal Toys公司將魔術方塊帶至全世界,並於1980年一、二月在倫敦、巴黎和美國的國際玩具博覽會亮相。
展出之後,Ideal Toys公司將魔術方塊的名稱改為Rubik's Cube,1980年5月,第一批魔術方塊在匈牙利出口[7]。
流行[编辑]
魔方廣為大眾喜愛是在1980年代。從1980年到1982年,總共售出了將近200萬個魔方。1981年,一個來自英國的小男孩,派翠克·波塞特(Patrick Bossert)寫了一本名叫《你也能夠復原魔方》(ISBN 978-0-14-031483-0)的書,總共售出了將近150萬本[7]。據估計,1980年代中期,全匈牙利有五分之一的人在玩魔術方塊[6]。
更多種類的魔術方塊[编辑]
由於魔方的巨大商機,1983年魯比克教授和他的合夥人一同開發了二階和四階魔方[8]。並於1986年製造了五階魔方[9]。
2003年,希臘的Panagiotis Verdes申請了五階到十一階魔術方塊的專利(五階魔術方塊的結構略與魯比克教授的魔術方塊不同),並於2008年在V-Cube公司生產五階、六階和七階的魔術方塊。
许多中国公司生产了复制或者改进的鲁比克版本或者V-Cube公司版本的魔方。其中最有名的是包大庆的大雁公司,他们生产孤鸿、凌云、轮回、展翅以及现在的腾云型号。但是相较于原始版本的产品,其较佳的转动性能使得许多专家级别的竞速玩家更愿意使用。另外,後來也有許多魔方公司相繼崛起,如奇藝魔方格以及其子公司the valk、魔域文化的魅龍、魔方教室系列、裕鑫方塊、永駿魔方、Gan方塊等等。其中,又以Gan的價格最高。[來源請求]
比賽[编辑]
根據金氏世界紀錄第一場魔方比賽於1981年3月13日,第一名是慕尼黑出生的Jury Froeschl,花了38秒。
第一個國際性的比賽於1982年6月5日在布達佩斯舉行,當時的比賽項目只有速解魔術方塊,第一名是Minh Thai,花了22.95秒,之後又逐漸增加了其他比賽規則。
- 2003年起,世界魔術方塊協會開始定期舉辦比賽,並記錄了1982年和2003年之後正式比賽的最佳成績[10]。
- 2004年,WCA使用較精準的Stackmat計時器來計時,增加比賽的準確性。
- 2007年,法國的Thibaut Jacquinot以9.86秒的成績成為首個在10秒內復原魔術方塊的人。
- 2013年,荷蘭的Mats Valk以5.55秒的成績成為當時最快復原魔術方塊的人。
- 2015年,美國高中生Collin Burns以5.253秒的成績成為當時最快復原魔術方塊的人。
- 2015年11月,美國的Lucas Etter以4.904秒的成績成為當時最快復原魔術方塊,且為首位在5秒內復原魔術方塊的的人。
- 2017年,韓国的Seung Beom Cho以4.59秒記錄成為當時最快復原魔術方塊的人。
- 2018年,澳大利亞的菲利克斯·曾姆丹格斯以4.221秒記錄成為當時最快復原魔術方塊的人。
- 2018年11月,中國大陸的杜宇生以3.475秒的成績成為當時最快復原魔術方塊,且為首位在4秒內復原魔術方塊的人。
- 2023年6月,美國的馬克斯·朴以3.134秒的成績成為目前最快復原魔術方塊的人,領先前紀錄0.341秒。
細節[编辑]


配色[编辑]
其實魔術方塊並不只有一種配色,現在所流行的是官方版本,事實上也還有其他版本的配色 (非官方標準六色的方塊不在以下討論範圍中)。
日本配色[编辑]
日本配色是魯比克教授最初研發出魔術方塊時的配色,分別為白色、紅色、橘色、黃色、綠色、藍色,其中白藍相對、紅橘相對、黃綠相對,且橘、藍、紅三色以逆時针排列。
在魔術方塊傳至全世界後,魯比克公司聽取色彩研究者的意見,將配色做了更改,但日本則維持原來的配色
官方配色[编辑]
魯比克公司聽取色彩研究者的意見,將相對兩面的顏色安排為相同色系,也就是白黃相對、紅橘相對、藍綠相對,且藍、橘、黃三色以順時鐘排列。
V-Cube公司配色[编辑]
V-Cube公司的配色與魯比克公司的配色相似,只是將白色換成黑色,即黑黃相對、紅橘相對、藍綠相對,且藍、橘、黃三色以順時鐘排列。
其他配色[编辑]
粉色配色,桃色(洋紅色),青色(天藍色),紫色,灰色來代替原本六色中的顏色。
韩国配色[编辑]
在韩国的比赛中,一般采用黑黄,蓝绿,红橙的配色标准。
結構[编辑]
不同的魔術方塊有不同的結構,以最經典的三階魔方為例,三階魔方由1個中心軸/核心球、6個中心塊、12個邊塊及8個角塊構成,當它們組合在一起的時候每個零件會互相牽制不會散開,並且任何一面都可水平轉動而不影響到其他方塊。三階魔方的結構不只一種,例如空心魔方。中国的一些魔方玩家,尝试对三阶魔方结构进行修改,形成适合竞速的魔方,这些修改包括对摩擦面接触方式、尺寸、重量、材质、颜色、边角处理、弹簧弹力等等的修改,这些修改都很成功,還有一些磁吸或者軸心透過磁斥讓手感阻力減少的設計,受到了世界魔方顶尖选手的青睐。不过这些魔方在中国以外的地区,依然会面对三阶魔方结构专利权的问题。[來源請求]
-
三階魔方結構
-
四階魔方拆解零件
-
五階魔方拆解零件
魔方公式書寫方式[编辑]

為了記錄下復原、轉亂的過程或公式的步驟,會用Singmaster符號來書寫(由David Singmaster發明)[11]。書寫方式如下:
- R(Right)、L(Left)、U(Up)、D(Down)、F(Front)、B(Back)分別代表右、左、上、下、前、後層。
- 若是順時针旋轉,則直接寫上符號;若是逆時针旋轉,則在符號後加上「'」或是「i」;若是旋轉180°,則在符號後加上「2」或是「²」。
若要更加詳細紀錄整個過程,還會使用以下符號:
- x、y、z分別代表將整個魔術方塊做R、U、F,因為在速解魔術方塊的時候,並不會總是將一個面朝向自己。
- r、l、u、d、f、b分別代表右、左、上、下、前、後兩層,代表連中間層一起轉。
- M(Middle)、E(Equator)、S(Side)代表旋轉中間層,相當於Rr'、Uu'、Bb'[12](注意x, y, z和M, E, S對應的方向不一樣)。
延伸[编辑]
魔方家族的成員有很多,以下用中心軸的數量分布來分類。若每個中心軸都是等價的(即對稱性較高),則軸的數量有可能是4、6、8、12、20、32,因為正多面體具有高度的對稱性,不同的軸數則對應到不同的正多面體,在這之中四軸、六軸和十二軸又較為常見。另外也有些魔方的中心軸不等價,例如Square 1。以下列出的是較常見的魔方。
四軸魔術方塊[编辑]
這一類魔方具有四個等價的中心軸,其中較常見的是鑽石魔方、金字塔魔方。
鑽石魔術方塊[编辑]
原名Skewb Diamond,是一種具有八面體結構的魔術方塊。一共有8個面塊及6個角塊,每一次移動可以旋轉4個面塊及3個角塊120°或-120°,與斜轉方塊、終極斜方具有相似的結構。
 |
 |
 |
鑽石魔方的中心塊 = 斜轉方塊的角塊 = 終極斜方的小塊。
鑽石魔方的角塊 = 斜轉方塊的中心塊 = 終極斜方的大塊[13]。
钻石魔方还有许多其他不同的变化形态,还原的方法也不尽相同。
金字塔魔方[编辑]

金字塔魔術方塊(Pyraminx)是一種四面體魔術方塊,由德国科学家麦菲特(Uwe Meffert)教授于1970年发明。三阶的金字塔魔方有四個外角塊、四個內角塊和六個邊塊。通過旋轉可以改變其顏色排列。軸旋轉塊可以旋轉後而狀態不改變。6個邊塊則可以自由旋轉。而四個頂塊可以獨立於其他塊進行自我旋轉。 作为最简单的异形魔方,金字塔魔方的还原是多种多样的。对于初学者来说,使用层先法较易还原。方法就是先还原魔方的四面中心块,再一面面复原。
六軸魔術方塊[编辑]
這一類魔方具有六個等價的中心軸,其中較常見的是n×n×n的魔術方塊,但外型不一定會做成立方體,例如:七階魔方。實際上,七階以上的魔術方塊是無法做成每小塊同大小的立方體的。

二階魔術方塊[编辑]
二階魔方的英文官方名字叫做Pocket Rubik's Cube或Mini Cube,中文直譯叫做「口袋魔方」、「迷你魔方」。與二阶粽子魔方(Pyramorphix 具有相似的結構。
Pyramorphix雖然有4個面塊和4個角塊,但每塊都和二階魔方一樣是等價的,每一次移動可以旋轉2個面塊及2個角塊±90°或180°。Pyramorphix與二階魔方的關係類似立方體和正三角形的關係[14]。

三階魔術方塊[编辑]
即一般的魔術方塊。另外有魔粽(Mastermorphix)、镜面魔方(Mirror)等變形。
鏡面魔方[编辑]
镜面魔方是较为常见的异形魔方,是三阶魔方的变种。其六个面的颜色一致,但厚度各不相同。还原方法与三阶魔方相同。 因为形状会发生变化,而且在形态识别没有普通带有颜色区别的魔方这么快,而且各块形状不均匀,因此不太适合于速拧,并未列入世界魔方协会(WCA)的比赛项目。
在还原过程中,镜面魔方与传统6色魔方不同,传统6色魔方是上下左右前后各为一种不同的颜色,我们在还原的时候,是以颜色来确定魔方块应该在的位置。而镜面魔方,所有的块儿都是同一个颜色的,整个魔方体只有一种颜色,而不规则的切割让魔方每一块都具有不同的形状,我们在进行还原的时候,是以不同的形状块来确定它应该回到的位置。 一般的,因为结构相同,如果会玩三阶魔方就会玩镜面魔方,只是由本来识别颜色,改为识别形状。
四階魔術方塊[编辑]
四階魔方的英文官方名字最初稱作為Sebestény Cube,後來在生產前最終定名為Rubik's Revenge,直譯過來是「鲁比克的復仇」。
五階魔術方塊[编辑]
五階魔方的英文名字叫做Professor's Cube,直譯過來是「專家(玩)的魔方」,也說明了它的難度。另外希臘的V-Cube公司也製造了不同結構的五階魔方,英文名字叫做V-Cube 5[15]。
六階魔術方塊[编辑]
六階魔術方塊首先由希臘的V-Cube公司量產[15],v-cube公司的產品未能妥善解決隠藏中層定位的問題,容易卡死。第一款能正常工作的六階魔術方塊由中国的圣手公司量產,以台湾玩家xb27改装的結構解決隠藏中層定位的問題。現時所有量產形6階的棱塊大部分不是正方,加強結構強度。
七階魔術方塊[编辑]

七階魔術方塊首先由希臘V-Cube公司量產[15]。方塊本身為圓弧型。第一款方形七階由中国圣手公司生產,棱塊是長方形。
八階或以上魔方[编辑]
八阶到十一阶魔方由希腊的V-Cube公司提出第一個设计概念。該概念在八阶(包括六阶)等偶数阶魔方均采用的是相应高一阶的奇数阶魔方的结构,通过隐藏中心层来实现,但未能妥善解決隐藏中心层的走位。因此用V-Cube设计的偶数阶魔方即使制造出来,其手感并不好,容易卡死和飞块(POP)。其後出現的設計有双層卡腳甚至三层卡脚,大幅加強穏定性。也出現了"加針"和"隐藏二階"等方法來解決中層走位。
數學上七阶以上的魔方已经无法做成梭、角、心块均匀的正方体。因为阶数过高会导致角上的块完全悬挂于魔方之外而难以固定。因此理论上,角块要做的非常大,边块做成长方形,而中心块则是非常小的正方形,有廠家把以这方法做出了方形的8階。由於六階角塊跟主体的連接處不能太小,不然結構強度不足,所有量產方形六階棱塊都是長方形的。部份廠家把高阶魔方做成面包形,减轻了魔方块的大小在视觉上的差异,方便手持。
八阶魔術方塊由中国圣手公司設計,已量產上市。
九阶魔術方塊中国于2009年12月8日产出首批,现已上市销售。

十阶魔術方塊由中国圣手公司設計,已量產上市。
十一阶魔術方塊大约于2010年1月在中国国内上市销售。
十三阶魔術方塊由中国永骏公司设计,大约于2014年1月在中国国内上市销售。
目前阶数最高实物魔方是三十三阶。
另外,在電腦中沒有結構的限制,二十階甚至几万階的魔術方塊電腦都可以模擬出來。
空心魔術方塊[编辑]
空心魔方是一種魔術方塊,由日本的冈本胜彦发明,一般以三阶为主,结构与三阶魔方不同。由于没有中心块,所以复原比三阶的难。
八軸魔術方塊[编辑]
這一類魔方具有八個等價的中心軸,其中較常見的是Dino Cube、Platypus、Rainbow Cube、魔花魔方。
十二軸魔術方塊[编辑]
這一類魔方具有十二個等價的中心軸,其中較常見的是五魔術方塊、亞歷山大之星、Pyraminx Crystal、直升機方塊。
五魔術方塊[编辑]

五魔術方塊(英文: Megaminx,簡稱五魔方或五魔),是一種十二面體魔術方塊,總共有50塊可以移動的部分。是世界魔方協會的比賽項目之一。
與六軸魔術方塊一樣,可以增加層數,目前最高階的五魔術方塊是由Andrew Cormier製造並販售,每一個軸有三個地方可以轉動,總共有530塊可以移動的部分[16][17]。
亞歷山大之星[编辑]

亞歷山大之星的原名為Alexander's Star,外型為大十二面體,是亞當·亞歷山大於1982年發明的魔術方塊,於1985年申請美國專利第4,506,891号,其結構可視為只有邊塊的五魔術方塊。
十二軸菱形十二面體[编辑]

十二軸菱形十二面體魔術方塊是一種菱形十二面體的魔術方塊,總共有38塊可以移動的部分,分別有8個三色角塊、6個四色角塊和24個中心面塊,一共有十二種顏色。這種方塊允許混元轉動(jumbling move),因此可以轉成特殊形狀。
直升機方塊[编辑]

直升機方塊同樣也是一種十二軸的魔術方塊,其軸分布與十二軸菱形十二面體相同,外觀有如二階魔術方塊和斜轉魔術方塊的組合,但實際切割方式不同。[18]這種方塊是一個立方體魔術方塊,但與一般的立方體魔術方塊不同:一般的立方體魔術方塊是以面轉動為主,而直升機方塊則是以稜轉動為主。這種方塊同樣允許混元轉動(jumbling move),因此可以轉成非立方體的型態。直升機魔術方塊由亞當·G·考恩(Adam G. Cowan)於2005年發明,並於2006年建造出來。[19]
多軸魔術方塊[编辑]
這一類魔方具有十二個以上等價(或不等價)的中心軸,具代表性的例子是Tuttminx,有32軸。
Tuttminx[编辑]

這種比較特別,外型為半正多面體中的截角二十面體,共有32軸,截至2016年,軸數最多的魔術方塊。
其他魔方[编辑]
這類魔方不具有等價的旋轉軸,較常見的是Square 1、Floppy Cube。
Square one[编辑]

Square One又叫做Square1或者SQ1,是由Karel Hrsel和Vojtech Kopsky在1992年共同發明並申請了美國專利第5,193,809号。它的難度主要在於上下兩個地面的方塊被切割成了可以轉動30度的小塊,從而可以產生不同于原始方方正正模樣的狀態。
Square 1魔術方塊分為三層。頂層和底層都有風箏塊和三角塊,它們也被稱為角塊和邊塊。整個魔術方塊總共有8個角塊和8個邊塊。相對於層的中間來講,角塊為60度,邊塊寬度為30度。
電子魔術方塊[编辑]

E-CUBE電子魔方[编辑]
世界上第一個量產的3階電子魔術方塊,由台灣學樂公司推出由台灣龍華科大邱煌森老師授權生產。使用三色LED顯示及按鍵操作,在每個行列上都有兩個按鍵,使用者經由壓觸按鍵選擇旋轉方向,而LED的顏色變化模擬原機械式魔方的旋轉。因為是微控制器軟體控制,因此使用者可以輕易的恢復原始狀態及設定開始難易程度,E-cube也加入其他遊戲的功能。雖然產品早已量產及販賣,但正式於媒體亮相是在2008年10月30日的台灣教育部舉辦產學展覽會上。
魔方的Mod制造[编辑]
魔方的改造由来已久,其中以英国的Tony Fisher最为著名,中国的包大庆(大烟头)等玩家也对其进行了发扬,但是这是一项难度较大的工程,对魔方需要有很深的认识,否则会毁坏掉魔方,所以,专攻此项的人较少,不过新手还是可以对魔方进行简单改造(比如连体,切割等)
世界魔方協會(WCA)[编辑]
魔方同樣有自己的世界組織世界魔方協會(World Cube Association簡稱WCA),這個協會是被承認的關於魔方的官方組織。它致力於推廣魔方,同時也舉辦各種比賽,並且收錄最好的成績作為官方的世界紀錄。
官方承認的紀錄有:[10]
- 二、三、四、五、六、七階單次最快和平均速度
- Megaminx、Pyraminx、Square 1、Rubik's Clock、Skewb單次最快和平均速度
- 三階單擰、三階腳擰單次最快和平均速度(腳擰於2019年被取消)
- 三階最少步數
- 三、四、五階盲擰
- 三階多個盲擰(新、舊)
- 魔板、大師魔板單次最快和平均速度(於2013年被取消)
其中三階多個盲擰(舊)已非官方比賽項目,新式的規則是:一小時內盲擰多少魔術方塊[12]。
玩法、比賽規則[12][编辑]
速解[编辑]
即用最短的時間復原一個魔方。一般來說,轉動次數越少復原的速度越快,但相對的需要記憶的公式就越多。較爲入門的解法為逐層復原的層先法 ( LBL,Layer by Layer ),而現在絕大多數魔術方塊高手使用的解法是略爲進階的CFOP(Fridrich Method),該解法名稱取自其四個主要步驟的首字母縮略字,即底十字(Cross)、下兩層(F2L)、頂層定向(OLL)、頂層排列(PLL)。更進階的延伸解法為zbll,將OLL和PLL一次完成,共302條公式。另一個較主流的速解法為Roux Method,又稱橋式,是由法國人Gilles Roux提出,特色是公式量少,復原步驟較短,思路靈活,復原過程會有大量的中層轉動。在速解魔方時,一般要使用專業的速解魔方來減少不必要的卡頓提高速解魔方的效率。目前主流的速解魔方有:GAN CUBE,奇藝魔方格,魔域文化等等。
盲解[编辑]
又稱作BLD。規則是在不做物理標記和轉動魔方(可以手握魔方)的前提下記憶一個或多個打亂的魔方,但在復原的過程中必須帶著眼罩。計時是從看到魔方的第一眼開始的,也就是說記憶魔方的時間也算在復原時間內。如果有零件在轉動過程中脫落(pop),也要在蒙眼的情況下裝回去。
單手解[编辑]
即以單手轉動魔方進行復原,但可以使用桌面輔助。如果有零件在轉動過程中脫落(pop),也必須用同一隻手裝回去。通常右撇子使用左手復原,而左撇子反之。
腳解[编辑]
即用腳復原魔術方塊,參賽者可以站立、坐在椅子上或地上。觀察的部分也必須用雙腳完成,其他規則大致與競速玩法相同。2020年已被WCA废除。
最少步驟還原[编辑]
在這此比賽中,參賽者必須在60分鐘內,遞交指定某3x3方塊的解法。以解法的步數長短做為比賽依據。參賽者可以使用紙、筆、三個魔術方塊和貼紙來輔助思考與作答。
多顆盲解[编辑]
規則大致與一般盲解相同,但必須同時記憶多個魔術方塊,在比賽時必須先告知裁判要復原幾個魔術方塊,每多一顆復原的時間為可加10分鐘,上限一小時(例如:欲挑戰三顆,總復原時間最長為卅分鐘;欲挑戰七顆者仍為一小時)。舊式規則沒有限定總時間,新式規則限定所有的復原必須在一小時內完成(記憶的時間算在內)。排名的依據為(成功顆數-失敗顆數),如有同分再依時間長短排序。
基于深度学习和量子力学的解决方案[编辑]
魔方已通过强化学习算法解决,该算法利用基于量子力学的魔方的数学描述。
觀察[编辑]
在WCA的官方比賽中,速解不管是單手解或雙手解都可以先觀察15秒。觀察前由官方準備的紙盒蓋住,選手再自行告知裁判何時開蓋觀察,開始後,裁判便會用碼表紀錄觀察時間。觀察時選手可以拿起方塊但不可轉動方塊,裁判會在時間過去8秒和12秒時通知選手,觀察時間結束後選手須將方塊放回桌上。 盲解的觀察則是會列入計時。 [20]
世界紀錄[编辑]
三階魔術方塊官方紀錄[编辑]
截至2024年4月7日的世界紀錄:[10]
| 項目 | 紀錄 | 保持者 | 國籍 | 比賽 |
|---|---|---|---|---|
| 3x3(單次) | 3.13秒 | Max Park | 美國 | Pride in Long Beach 2023 |
| 4.48秒 | Yiheng Wang (王艺衡) | 中國 | Mofunland Cruise Open 2023 | |
| 2x2(單次) | 0.43秒 | Teodor Zajder | 波蘭 | Warsaw Cube Masters 2023 |
| 0.92秒 | Zayn Khanani | 美國 | New-Cumberland County 2024 | |
| 盲解(單次) | 12.00秒 | Tommy Cherry | 美國 | Triton Tricubealon 2024 |
| 14.15秒 | Tommy Cherry | 美國 | Rubik's WCA World Championship 2023 | |
| 單手解(單次) | 6.20秒 | Max Park | 美國 | Marshall Middle Slice 2022 |
| 8.62秒 | Max Park | 美國 | Nub Open Mission Viejo 2023 | |
| 最少步數 (單次) | 16步 | Sebastiano Tronto | 意大利 | FMC 2019 |
| 20步 | Wong Chong Wen (黄崇文) | 新加坡 | FMC Johor Bahru 2023 | |
| 多個盲擰 | 62/65 57:47(57分47秒復原65顆裡面的62顆) | Graham Siggins | 美國 | Blind Is Back LA 2022 |
非官方紀錄[编辑]
- 奇安弗蘭科·烏安奇在水中盲擰成功復原四個魔方。
- Justin Adsuara在48.31秒內用筷子復原一個魔方。
- Rowe Hessler在24小時內,復原10000個魔方。
- Kevin Hays在水中憋氣,一口氣復原8個魔方。
- 最大的魔方:邊長3.52米,製造者為Daniel Urlings。
- 最貴的魔方:Masterpiece Cube,總共用了22.5克拉的紫水晶、34克拉的紅寶石和34克拉的綠松石,魔術方塊本身是用18K的黃金製造,造價大約為1,500,000美元[21]。
- 2017年,德國科技公司英飞凌製造了一台機器人,以0.637秒的時間打破了之前的紀錄。[22]
- 闕劍宇在五分鐘以內拋接解完了3顆魔方
魔方数学方程式[编辑]
變化數[编辑]
三階魔方的總變化數是:
三階魔方總變化數的算式是這樣得來:
- 8個角块可以互换位置(),也可以旋轉(),但不能單獨旋轉一個角塊,所以总共有种变化状态。
- 12个边块可以互换位置(),也可以翻轉(),但不能單獨翻轉一個邊塊(將兩個面對調),也不能單獨交換兩邊塊,所以总共有种变化状态。
也就是說,拆散魔術方塊再隨意組合,有的機率無法恢復原狀(角塊或邊塊被單獨翻轉)。
對於一個拆散又再隨意組合的魔術方塊,總變化數則是:
有些魔方在各个面的图案具有方向性,考虑到6个中心块各有4种朝向,但不能仅仅将一个中心块旋转90度,這時總变化数目还要再乘以。此时结果为:
製造的極限[编辑]
電腦與魔方[编辑]
- 用電腦解決魔方的復原問題並不是很困難,關鍵是要找到一個好的演算法。
- 目前速度最快且解決魔方平均步驟最少的軟體是Cube Explorer(页面存档备份,存于互联网档案馆)。[23]
上帝的數字[编辑]
所有的三階魔術方塊都可以在有限步數內復原,1982年,佛雷與辛馬斯特合著的《魔術方塊手冊》定義任意的三階魔術方塊都可以保證最少n步復原,並稱呼n為上帝的數字。在此書中,證明上帝的數字介於17~52之間。
1995年,瑞德證明上帝的數字介於20-29之間。2006年,雷杜用群論證明上界可改進為27。
2007年,電腦科學家古柏曼與他的學生用20台超級電腦花了8000個小時證明上界可改進為26。
2008年,Tomas Rokicki宣布证明了任何魔方可以在25步以内解开[24]。之後又改进为22步。
2010年,包括Tomas Rokicki和Morley Davidson等人的研究团队证明任意组合的魔方可以在20步内还原,现在上帝的數字正式定为20[25][26]。
對於世界的影響[编辑]
生活中的魔方[编辑]
電影中的魔方[编辑]
- 1987年,由恐怖小說作家克里夫·巴克(Clive Barker)執導的第一部電影《養鬼吃人》
- 1997年,由文森佐·內塔利(Vincenzo Natali)導演的加拿大科幻電影《異次元殺陣》
- 2006年,由威爾史密斯主演的《當幸福來敲門》
- 2008年,由迪士尼皮克斯製作的動畫《瓦力》
- 2008年,由丁晟导演的《硬汉》
- 2008年,由金镇英(Jin-young Kim)导演的《天才宝贝》
- 2009年,由约翰·塞纳(John Cena)主演的《十二回合》
- 2009年,由亚当·艾略特(Adam Elliot)导演的《玛丽和马克思》
- 2009年,由拉库马·希拉尼(Rajkumar Hirani)导演的《三个傻瓜》
- 2011年,由金石润导演的《朝鲜名侦探》
- 2011年,由马里奥·安德鲁西奥(Mario Andreacchio)导演的《寻龙夺宝》
- 2011年,由蕭敬騰主演的《殺手歐陽盆栽》
- 2012年,由安德魯·加菲爾德主演的《蜘蛛人:驚奇再起》
- 2016年,由喬瑟夫·高登-李維主演的《神鬼駭客:史諾登》
- 2018年,由史蒂芬·史匹柏執導的《一級玩家》
註釋[编辑]
- ^ William Fotheringham. Fotheringham's Sporting Pastimes. Anova Books. 2007: 50. ISBN 1-86105-953-1.
- ^ 'Driven mad' Rubik's nut weeps on solving cube... after 26 years of trying (页面存档备份,存于互联网档案馆), Daily Mail Reporter, 12th January 2009.
- ^ Daintith, John. A Biographical Encyclopedia of Scientists. Bristol: Institute of Physics Pub. 1994: 771. ISBN 0-7503-0287-9.
- ^ William Lee Adams. The Rubik's Cube: A Puzzling Success. TIME. 2009-01-28 [2009-02-05]. (原始内容存档于2013-08-26).
- ^ Alastair Jamieson. Rubik's Cube inventor is back with Rubik's 360. The Daily Telegraph. 2009-01-31 [2009-02-05]. (原始内容存档于2018-06-16).
- ^ 6.0 6.1 http://www.rubiks.com/World/Cube%20facts.aspx (页面存档备份,存于互联网档案馆)
- ^ 7.0 7.1 7.2 存档副本. [2009-08-20]. (原始内容存档于2017-06-08).
- ^ 二階魔術方塊美國專利第4,378,117号,四階魔術方塊美國專利第4,421,311号
- ^ 五階魔術方塊美國專利第4,600,199号
- ^ 10.0 10.1 10.2 WCA官方紀錄. 2009-08-16 [2009-08-24]. (原始内容存档于2009-03-18).
- ^ Joyner, David (2002). Adventures in group theory: Rubik's Cube, Merlin's machine, and Other Mathematical Toys. Baltimore: Johns Hopkins University Press. pp. 7. ISBN 978-0-8018-6947-1.
- ^ 12.0 12.1 12.2 WCA比賽規則. 2009-02-06 [2009-08-24]. (原始内容存档于2009-02-17).
- ^ [1] (页面存档备份,存于互联网档案馆)[2] (页面存档备份,存于互联网档案馆)鑽石魔方、斜轉方塊和終極斜方的關係
- ^ 立方體和正三角形的關係
- ^ 15.0 15.1 15.2 V-CUBE. [2008-06-30]. (原始内容存档于2008-04-30).
- ^ http://www.bedardpuzzles.com/index.php?puzzle/30 互联网档案馆的存檔,存档日期2012-11-09.
- ^ 存档副本. [2009-09-04]. (原始内容存档于2021-05-20).
- ^ 宋雨键. Jumble and Edge Turning Hexahedron (Axis System) Jumble 与菱 12 轴类魔方 (PDF). Nankai Cube Association.
- ^ Helicopter Cubes Black body. Mèffert's. [2010-09-01]. (原始内容存档于2011-07-14).
The Helicopter Cube was conceived by Adam G. Cowan in 2005, but wasn’t built until 2006, when Adam discovered that 3D printing could be used to realize the parts.
- ^ Corli, Sebastiano; Moro, Lorenzo; Galli, Davide; Prati, Enrico. Solving Rubik’s cube via quantum mechanics and deep reinforcement learning. Journal of Physics A: Mathematical and Theoretical. 2021, 54 (42): 425302. arXiv:2109.07199v1
 . doi:10.1088/1751-8121/ac2596.
. doi:10.1088/1751-8121/ac2596.
- ^ http://thelongestlistofthelongeststuffatthelongestdomainnameatlonglast.com/expensive70.html. [2009-08-25]. (原始内容存档于2009-08-28). 外部链接存在于
|title=(帮助) - ^ 0.637 seconds - a new Rubik's Cube machine world record! 德國英飛凌科技股份有限公司打破世界紀錄 (页面存档备份,存于互联网档案馆)。
- ^ Team, Discuz! Team and Comsenz UI. 魔方小站论坛 最新版Cube Explorer 4.64简体中文90%汉化版新鲜出炉!!由本人亲自汉化 魔方教程|魔方视频|魔方玩法|魔方公式 - Powered by Discuz!. bbs.rubik.com.cn. 魔方小站论坛. [2017-05-16]. (原始内容存档于2021-05-20).
|author1=和|last1=只需其一 (帮助) - ^ Tom Rokicki. Twenty-Five Moves Suffice for Rubik's Cube (PDF). [2008-03-24]. (原始内容存档 (PDF)于2021-05-20).
- ^ Solidot - 魔方的终结还原步数是20步. [2010-08-09]. (原始内容存档于2017-11-07).
- ^ God's Number is 20/. [2010-11-15]. (原始内容存档于2013-07-21).
參考條目[编辑]
參考文獻[编辑]
- World Cube Association Official Results (页面存档备份,存于互联网档案馆)
- Handbook of Cubik Math by Alexander H. Frey, Jr. and David Singmaster
- Notes on Rubik's 'Magic Cube' ISBN 978-0-89490-043-3 by David Singmaster
- Metamagical Themas by Douglas R. Hofstadter contains two insightful chapters regarding Rubik's Cube and similar puzzles, originally published as articles in the March 1981 and July 1982 issues of Scientific American.
- Four-Axis Puzzles by Anthony E. Durham.
- Mathematics of the Rubik's Cube Design ISBN 978-0-8059-3919-4 by Hana M. Bizek
- 柯利弗德·皮寇弗; 陳以禮(翻譯). The Math Book:From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics [數學之書]. 時報文化. 2013-04-16. ISBN 978-957-135-699-0 (中文(繁體)).
外部連結[编辑]
| 维基共享资源上的相关多媒体资源:魔方 |
- 魔方攻略 (页面存档备份,存于互联网档案馆)
- 魯比克魔方的官方首頁 (页面存档备份,存于互联网档案馆)
- Meffert (页面存档备份,存于互联网档案馆)
- 世界魔方協會官方主頁 (页面存档备份,存于互联网档案馆)
- speedcubing (页面存档备份,存于互联网档案馆)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||