泊松过程

跳过字词转换说明

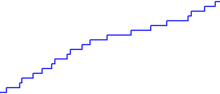
Poisson过程（Poisson process，大陆译泊松过程、普阿松过程等，台译卜瓦松過程、布瓦松過程、布阿松過程、波以松過程、卜氏過程等），是以法國數學家泊松（1781 - 1840）的名字命名的。泊松過程是隨機過程的一種，是以事件的發生時間來定義的。我們說一個 隨機過程 N(t) 是一個時間齊次的一維泊松過程，如果它滿足以下條件：

• 在兩個互斥（不重疊）的區間內所發生的事件的數目是互相獨立的隨機變數。

• 在區間$[t,t+ \tau]$內發生的事件的數目的機率分佈為：

$P [(N(t+ \tau) - N(t)) = k] = \frac{e^{-\lambda \tau} (\lambda \tau)^k}{k!} \qquad k= 0,1,\ldots$

其中λ是一個正數，是固定的參數，通常稱為抵達率（arrival rate）或強度（intensity）。所以，如果給定在時間區間$[t,t+ \tau]$之中事件發生的數目，則隨機變數$N(t + \tau) - N(t)$呈現泊松分布，其參數為$\lambda\tau$。

更一般地來說，一個泊松過程是在每個有界的時間區間或在某個空間（例如：一個歐幾里得平面或三維的歐幾里得空間）中的每一個有界的區域，賦予一個隨機的事件數，使得

• 在一個時間區間或空間區域內的事件數，和另一個互斥（不重疊）的時間區間或空間區域內的事件數，這兩個隨機變數是獨立的。

• 在每一個時間區間或空間區域內的事件數是一個隨機變數，遵循泊松分布。（技術上而言，更精確地來說，每一個具有有限測度的集合，都被賦予一個泊松分布的隨機變數。）

泊松過程是Lévy過程（Lévy process）中最有名的過程之一。時間齊次的泊松過程也是時間齊次的連續時間Markov過程的例子。一個時間齊次、一維的泊松過程是一個純出生過程，是一個出生-死亡過程的最簡單例子。