均轮和本轮
| 此条目翻译品质不佳。 (2017年7月31日) |
本轮(epicycle,源自古希腊语:ἐπίκυκλος,字面是在圆之上,意思是在另一个圆圈之上运动的圆圈 [1]。)是在天文学的喜帕恰斯、托勒密[锚点失效]和哥白尼日心说中,用来解释月球、太阳和行星视运动的速度和方向的几何模型。特别是它解释了当时已知的五颗行星的视逆行运动。其次,它也解释了行星与地球视距离上的变化。
它最初是由佩尔加的阿波罗尼奥斯在纪元前3世纪末提出的。它由阿波罗尼奥斯和罗德岛的喜帕恰斯在纪元前2世纪发展,并广泛的使用。然后在公元2世纪,被底比斯的托勒密正式收录在《天文学大成》的天文著作中。。
古希腊的天文计算设备安提基特拉机械,已经运用了本轮(周转圆)的运动。使用四个齿轮计算月球的位置和相位。两个齿轮用来补偿(模拟)月球的偏心运动,使月球的运动非常接近于开普勒第二定律的椭圆轨道,即月球在近地点的移动速度快,在远地点的移动速度慢。
本轮周期工作的很好,非常准确,因为正如傅里叶分析后来显示的,具有足够数量的周转圆,任何平滑曲线都可以任意的精度近似。然而,他们不认同日心参考框架下的行星运动基本上是椭圆形的,而这导致发现重力遵循简单的平方反比定律可以更好地解释所有的行星运动。
概论[编辑]
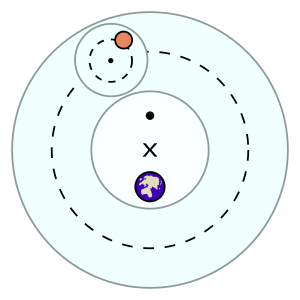
在喜帕恰斯和托勒密系统中,假设行星在一个称为本轮的小圆圈上移动,而小圆圈又沿着一个称为均轮的较大圆圈上移动。这两个圆都大致平行于太阳的轨道平面(黄道)顺时针旋转。尽管这个系统被认为是以地球为中心,但每颗行星的运动不是以地球为中心,而是以地球稍远,称为偏心的一个点为中心。在这个系统中,行星的轨道与外旋轮线相似。
在喜帕恰斯的系统中,行星在本轮上以均匀的顺时针运动沿着均轮自转和公转。然而,托勒密发现他无法调和巴比伦观测的数据,特别是在可见的逆行形状和大小上的差别。除非他从与偏心等距的另一点,他称为均衡点的位置上观察,否则本轮的角速度是不均匀的。从均衡点和地球之间的中心点(偏心)观察均轮的角速度是一个常数;只有从均衡点观察本轮的中心才能在相同的时间扫掠过相同的角度。托勒密系统与众不同的就是使用均衡点将本轮脱离均轮的中心点。
托勒密在《天文学大成》中没有预测行星均轮的相对大小。他的所有计算都是针对一个规范化的均轮完成的,每次只处理一个案例。这并不是说他认为行星都是等距的,只是除了月球之外,他没有任何依据可以测量行星的距离。他通常是根据行星的轨道周期从地球向外排列行星。后来,他在行星假设中计算了距离,并在本表的第一列概括了距离[2]:
| 天体 | 平均距离 (地球半径) |
现代值 (半长轴 地球半径) |
比率 (现代/托勒密) |
比率 (现代/托勒密 以太阳=1做标准) |
|---|---|---|---|---|
| 月球 | 48 | 60.3 | 1.26 | 0.065 |
| 水星 | 115 | 9,090 | 79.0 | 4.1 |
| 金星 | 622.5 | 16,980 | 27.3 | 1.4 |
| 太阳 | 1,210 | 23,480 | 19.4 | 1 |
| 火星 | 5,040 | 35,780 | 7.10 | 0.37 |
| 木星 | 11,504 | 122,200 | 10.6 | 0.55 |
| 土星 | 17,026 | 225,000 | 13.2 | 0.68 |
| 恒星层 | 20,000 | 不适用 | 不适用 | 不适用 |
如果他对均轮相对于地球-太阳的距离估计值更加准确,那么本轮的大小就会更接近地球-太阳的距离。虽然所有的行星都是分开考虑的,但以一种奇特的方式使它们都互相关联:所有经由行星本体通过本轮中心的线都与地球和太阳的连线平行,并且地球和太阳的连线也通过水星和金星的本轮中心。这意味着所有穿过行星和本轮中心的线都互相平行,并且也平行于地球和太阳的连线[来源请求]。
巴比伦的观测表明,外侧行星在夜空中的移动速度通常会比恒星慢。每天晚上,这颗行星似乎都落后于恒星,这称为顺行运动。在靠近冲的附近时,行星会出现相反方向的运动,并且在夜空中移动得比恒星快,在逆行运动一段时间后,会再次反转并恢复向前的运动。本轮理论,部分地试图在解释这种行为。
在观测上,内侧行星永远在太阳的附近,只在日出前不久或日落后不久短暂的出现在夜空。它们的视逆行运动发生在穿越地球和太阳之间,即昏星与晨星变换的过程。
历史[编辑]
当古代的天文学家注视天空时,他们看见太阳、月球和星星在头顶上以规律的型式运动,他们也看见"漫游者"或"planetai"(我们所谓的行星)。漫游者在运动上的规律表明,它们的位置可能也是可以预测的。

预测天体运动问题最简单的方法是根据星场绘制它们的位置,然后使用数学函数与不断变化的位置拟合[3]。
古人会建立地心说只有一个简单的原因,地球是它们立足和观察天空的场所,同时天空看起来是动的,而地球似乎依然很稳定的在脚下。一些希腊天文学家(例如西蒙的阿理斯塔克斯)推测行星(包括地球)环绕着太阳,但是光学(和具体的数学-例如艾萨克·牛顿的万有引力定律)必须提供令人信服的具体资料以支持日心说的模型。但直至托勒密死后1,500年的时代,这些都还不存在。此外,亚里士多德物理学在设计时并没有考虑到这些计算和性质,而且日心说的观念和亚里士多德天空是完美的哲学相违背。直到伽利略在1610年1月7日观测木星的卫星,和1610年9月观察金星的相位,日心模型才开始得到天文学家普遍的支持,同时也接受行星是环绕太阳的个别世界的看法(也就是地球是诸多环绕太阳的行星中的一颗)。约翰内斯·开普勒能够制定他著名的行星运动定律,以令人难以置信的准确度描述了太阳系中行星的轨道。开普勒的行星运动三定律今天依然在大学天文学和物理学中教授,而且这些定律的文字描述自开普勒在400年前制定以来,迄今都未曾改变。
天体的视运动相对时间有其周期性是很自然的。阿波罗尼奥斯意识到这种周期性变化可以通过小圆形轨道(本轮)在较大的圆形轨道(均轮)上旋转,在视觉上表示。喜帕恰斯计算了所需的轨道。
克劳狄乌斯·托勒密淬练了均轮和本轮的概念,并引入了均衡点做为计算行星运动速度变化的机制。他开发的实验证据方法,在当时被证明是非常准确的,并且在哥白尼和开普勒的时代都仍在使用。
欧文·金格瑞契[4]描述发生在1504年,很显然是由哥白尼观测的一次行星合。哥白尼在阿方索星表副本中的笔记评论说:"火星的位置超出2度以上,土星则落后了1.5度。"使用现代的计算机程序计算,金格瑞契发现在合的时刻,土星确实落后表中数值1.5度,火星则超前约2度。次外,他发现托勒密在当时对木星的预测相当准确。因此,哥白尼和与他同一时代的人都使用托勒密的方法来寻找行星,并在托勒密的原创作品出版一千多年后,发现它们还是可以信赖。
当哥白尼将基于地球观测的结果转为日心坐标时[5],他面临了一个全新的问题。以太阳为中心的位置显示了周期性的循环运动,但外行星没有逆行运动的循环。原则上,日心运动较为简捷,但由于尚未发现是椭圆轨道,因此尚不知其微妙之处。另一个并发的问题是由哥白尼从未解决的问体引起的:在坐标变换中正确核算地球的位置[6]。根据过去的经验,哥白尼在他的理论中继续使用均轮和本轮的模型,不同的是他的本轮很小,被称为 "小轮"(epicyclets)。
在托勒密的系统中,每颗行星的模型是不同的,所以哥白尼初始的模型也是如此。然而,当他通过数学完成时,哥白尼发现他的模型可以组合在一个统一的系统中。此外,如果调整它们的尺度,让地球和其他的行星有着一样的轨道,那末就很容易遵循数学上的结果排列出行星的顺序。水星在最接近太阳的轨道上运行,其余的行星依据公转轨道的周期,越长的排列在距离越远之处[7]。
虽然哥白尼的模型大大的降低了本轮的幅度,但它们是否比托勒密的模型简单是没有意义的。哥白尼消除了一些有伤害的均衡点,但代价是增加了额外的本轮。在16世纪,基于哥白尼和托勒密模型的书籍,使用的本轮数量是相等[8][9][10]。来自他自己一份未经发表,名为《评论》的文章中描述的陈述,他认为他的系统只需要34个圆圈(本轮)。但当他出版《天体运行论》时,他增加了更多的圆圈。计算圆圈的总数是困难的,但估计是他创造了一个一样复杂,甚至是更复杂的系统[11]。柯斯特勒(Koestler)在他《人类对宇宙的视觉史》中,等同于本轮的环有48个[12]。在1898年流行的托勒密系统,可能受到灵感来自欧多克索斯,使用77或79个球体,非托勒密系统的吉罗拉莫·弗拉卡斯托罗影响,圆圈的总数约为80个[13]。哥白尼在它的作品中夸大了托勒密系统使用的本轮数量;虽然托勒密系统最初的数量范围为80个圆圈,但根据哥白尼的年代,普尔巴赫(Purbach)已将托勒密系统更新为40个本轮;因此,哥白尼利用进一步的周期,有效的取代了逆行的问题[14]。
哥白尼的作品为逆行运动等现象提供了解释,但并不能证明行星实际上绕着太阳运行。哥白尼的理论至少和托勒密的一样准确,但从未达到托勒密理论的地位和认可。它所需要的是开普勒在1609年才发表的椭圆理论。

托勒密和哥白尼的理论证明了用均轮和本轮的装置代表行星运动的耐久性和适应性。由于太阳系异常轨道稳定性,使均轮和本轮模型的工作效果良好。假使哥特佛莱德·莱布尼兹和艾萨克·牛顿没有发明微积分,这两种理论现在还会在使用[15]。
第一个没有本轮的行星模型是在西班牙安达鲁斯的伊本·巴哲(阿文佩斯)在12世纪提出的[16],但直到17世纪,开普勒的椭圆轨道模型逐渐取代了哥白尼基于完美圆圈的模型,欧洲才消除了均轮和本轮。
牛顿或经典力学完全消除了对均轮和本轮方法的需求,并产生了更准确的理论。通过将太阳和行星视为质点,并使用牛顿的万有引力定律,推导出的运动方程,可以通过各种手段来计算行星的轨道速度和预测位置。简单的二体问题可以分析解决,复杂的N体问题需要数值分析来解决。
海王星的发现说明了牛顿力学解决轨道力学问题的能力。对天王星轨道中观察到的扰动进行分析,估计出这颗可疑行星的位置,给了发现行星一定程度上的位置参考。这不可能使用均轮和本轮来实现。尽管年顿在1702年出版的《月球运动理论》一书,它运用了一些本轮;中国一直使用到19世纪。基于牛顿的理论,后续的星历表精度可以到弧分[17]。
周转圆[编辑]
依据天文学史上的一个学派,通过长期累绩的观测,发现原始的托勒密系统有细微的缺陷。人们错误的认为,在模型中增加更多的圆(在圆内再增加圆﹚,就可以更准确的匹配观测到的行星运动。在16世纪,增加的环圈导致一个行不通而几乎无法运作的系统,哥白尼创造的日心系统,简化了当时的托勒密天文学,从而成功的大量减少环圈的数量。
随着更精确地观测,更多的环圈和偏心被用来解释新观测到的现象。到了中世纪后期,宇宙成为一个球体与许多中心和偏心泛滥的轨道,循环和周转圆充斥在天球的轨道上。
以复杂性作为衡量的标准,托勒密的环圈数多达80个,哥白尼只有34个[19]。1960年代的《大英百科全书》,对天文学的讨论中出现数量最多的是13世纪的卡斯提尔的国王阿方索十世(阿方索星历表被认为是他创建的。﹚
到这个时候,每颗行星都需要40到60个周转圆,才能描述它在星空之间复杂的运动。阿方索对这个项目的困难感到惊讶,他感叹的说,如果由他来创造,他可能会给更佳的建议。
——大英百科全书,1968年 [20]
事实证明,周转圆理论的一个主要困难是,历史学家在研究中世纪汉文一复兴时期的托勒密天文学书籍时,发现每颗行星绝对全都没有使用多个周转圆的痕迹。情况显然是,阿方索星历表显然是使用了托勒密最初未经修饰的方法计算的[21]
另一个问题就是模型本身不鼓励修补。在均轮和本轮的模型中,整体部分是相互关联的。参数的更改,可以改善在一个位置的拟合,但在某些地方又会不合。托勒密的模型在这方面可能是最佳的。总的来说,它给了一个好的结果,但在各处都少许有一点误差。有经验的天文学家会认识到这些缺点,并容许它们的存在。
数学形式主义[编辑]
在天体物理学或观测天文学的任何分支之中,既不是双边对称,也不是偏心周期的曲线,可以平滑的绘制出行星在星座内周期性运动转折的结果,但围绕一个个定的均轮,该周期在数量上是有限的。
——诺伍德·罗素·汉森,"数学在周转圆天文学的功能",1960[22]
任何路径,无论有无周期、封闭或开放,都可以用无限数量的周转圆表示。
这是因为周转圆可以表示为复杂的傅里叶级数;因此,对于大量的周转圆,复杂的路径,可以在复平面中表示[23]
让复数
此处的a0和k0 是常数, i = √−1是虚数单位,和t是时间,对应于以复平面的原点为中心,半径为a0的均轮和角速度为
此处T是周期。
如果z1是一个周转圆的路径,然后均轮加上本轮表示为总和
这是一个概周期函数,并且当比率常数kj是一个有理数时,则是一个周期函数。归纳为N个周转圆,则概周期函数
当每个kj都是有理数时,这就是周期性的。寻找系数aj在复平面上与时间相关的路径z = f(t),目标是克隆均轮和本轮的轨道,这是一种科学模式(σώζειν τα φαινόμενα)[24]。
相关条目[编辑]
注解[编辑]
- ^ "epicycle" (页面存档备份,存于互联网档案馆). Online Etymology Dictionary.
- ^ Andrea, Murschel. The Structure and Function of Ptolemy's Physical Hypotheses of Planetary Motion. Journal for the History of Astronomy. 1995, (xxvii): 33–61 [2014-08-02]. Bibcode:1995JHA....26...33M. (原始内容存档于2021-07-15).
- ^ For an example of the complexity of the problem, see Owen Gingerich, The Book Nobody Read, Walker, 2004, p. 50
- ^ Gingerich, Chapter 4
- ^ One volume of De Revolutionibus was devoted to a description of the trigonometry used to make the transformation between geocentric and heliocentric coordinates.
- ^ Gingerich, p. 267
- ^ Gingerich, p. 54
- ^ Palter, Robert. Approach to the History of Astronomy. Studies in the History and Philosophy of Science. 1970, 1: 94.
- ^ Owen Gingerich, "Alfonso X as a Patron of Astronomy", in The Eye of Heaven: Ptolemy, Copernicus, Kepler (New York: American Institute of Physics, 1993), p. 125.
- ^ Gingerich, "Crisis versus Aesthetic in the Copernican Revolution", in Eye of Heaven, pp. 193–204.
- ^ "The popular belief that Copernicus's heliocentric system constitutes a significant simplification of the Ptolemaic system is obviously wrong ... [T]he Copernican models themselves require about twice as many circles as the Ptolemaic models and are far less elegant and adaptable." Neugebauer, Otto. The Exact Sciences in Antiquity 2. Dover Publications. 1969 [1957] [2020-09-18]. ISBN 978-0-486-22332-2. (原始内容存档于2020-08-14)., p. 204. This is an extreme estimate in favor of Ptolemy.
- ^ Koestler, Arthur. The Sleepwalkers. Arkana, Penguin Books. 1989 [1959]., p. 195
- ^ Palter, Approach to the History of Astronomy, pp. 113–114.
- ^ Koestler, Arthur. The Sleepwalkers. Arkana, Penguin Books. 1989 [1959]., pp. 194–195
- ^ A deferent/epicycle model is in fact used to compute Lunar positions needed to define modern Hindu calendars. See Nachum Dershovitz and Edward M. Reingold: Calendrical Calculations, Cambridge University Press, 1997, Chapter 14. (ISBN 0-521-56474-3)
- ^ Goldstein, Bernard R. Theory and Observation in Medieval Astronomy. Isis. 1972, 63 (1): 39–47 [40–41]. doi:10.1086/350839.
- ^ Kollerstrom, Nicholas. Newton's Forgotten Lunar Theory. Green Lion Press. 2000. ISBN 1-888009-08-X.
- ^ Dorothy Stimson,
 The Gradual Acceptance of the Copernican Theory of the Universe (New York, 1917),
The Gradual Acceptance of the Copernican Theory of the Universe (New York, 1917),  p. 14. The quotation is from John Milton's Paradise Lost, Book 8, 11.82–85.
p. 14. The quotation is from John Milton's Paradise Lost, Book 8, 11.82–85.
- ^ Robert Palter, An Approach to the History of Early Astronomy
- ^ Encyclopædia Britannica, 1968, vol. 2, p. 645. This is identified as the highest number in Owen Gingerich, Alfonso X. Gingerich also expressed doubt about the quotation attributed to Alfonso. In The Book Nobody Read (p. 56), however, Gingerich relates that he challenged Encyclopædia Britannica about the number of epicycles. Their response was that the original author of the entry had died and its source couldn't be verified.
- ^ Gingerich, The Book Nobody Read, p. 57
- ^ Hanson, Norwood Russell. The Mathematical Power of Epicyclical Astronomy (PDF). Isis. 1960-06-01, 51 (2): 150–158 [2011-10-21]. ISSN 0021-1753. JSTOR 226846. doi:10.1086/348869. (原始内容存档 (PDF)于2020-11-01).
- ^ See, e.g., this animation (页面存档备份,存于互联网档案馆) made by Christián Carman and Ramiro Serra, which uses 1000 epicycles to retrace the cartoon character Homer Simpson; cf. also Christián Carman's "Deferentes, epiciclos y adaptaciones (页面存档备份,存于互联网档案馆)." and "La refutabilidad del Sistema de Epiciclos y Deferentes de Ptolomeo" (页面存档备份,存于互联网档案馆).
- ^ Cf. Duhem, Pierre. To save the phenomena, an essay on the idea of physical theory from Plato to Galileo. Chicago: University of Chicago Press. 1969. OCLC 681213472. (excerpt (页面存档备份,存于互联网档案馆)).
外部链接[编辑]
- Ptolemaic System(页面存档备份,存于互联网档案馆) – at Rice University's Galileo Project
- Eccentrics, Deferents, Epicycles, and Equants(页面存档备份,存于互联网档案馆) at MathPages
动画、插图[编辑]
- Java simulation of the Ptolemaic System – at Paul Stoddard's Animated Virtual Planetarium, Northern Illinois University
- Epicycle and Deferent Demo – at Rosemary Kennett's website at the University of Syracuse
- A flash animation showing epicycles with adjustable parameters and presets for various planets.(页面存档备份,存于互联网档案馆)
- An Applet showing the principle of the epicycle(页面存档备份,存于互联网档案馆), with a side-by-side comparison of the geocentric and heliocentric models.
- An excellent presentation on Ptolemy, Copernicus, Brahe and Kepler(页面存档备份,存于互联网档案馆), based on Kepler's writings. Part 1 examines the different systems and their equivalence, Parts 2 and onwards examine Kepler's derivation of his laws.
- Ptolemy and Homer (Simpson)(页面存档备份,存于互联网档案馆) Reconstruction of a planet's bizarre orbit with Ptolemy's system of epicycles and deferents.
| ||||||||||||||||||||||||||||||||




