前推 (微分)

  本文考慮微分幾何中的前推算子，由光滑流形間的光滑映射的微分誘導。關於術語「前推」在數學中的其他使用，參見前推。

假設 φ : M → N 是光滑流形之間的光滑映射；則 φ 在一點 x 處的微分在某種意義上是 φ 在 x 附近的最佳線性逼近。這可以視為通常微積分中全導數的推廣。確切地說，它是從 M 在 x 處的切空間到 N 在 φ(x) 處的切空間的一個線性映射，從而可以將 M 的切向量「前推」成 N 的切向量。

映射 φ 的微分也被一些的作者稱為 φ 的導數或全導數，有時它自己也之稱為前推（pushforward）。

動機

設 φ:U→V 是從 R^m 的一個開集 U 到 Rⁿ 的開集 V 的一個光滑映射。對任何 U 中的給定點 x， φ 在 x 的雅可比矩陣（關於標準坐標）是 φ 在 x 的全微分的矩陣表示，這是一個從 R^m 到 Rⁿ 的線性映射：

$\mathrm {d} \varphi _{x}:\mathbb {R} ^{m}\to \mathbb {R} ^{n}\ .$

我們希望將其推廣到 φ 是「任何」兩個光滑流形 M 與 N 之間的光滑映射。

光滑映射的微分

令 φ : M → N 是光滑流形間的光滑映射。給定某點 x ∈ M，φ 在 x 的微分或（全）導數是從 M 在 x 的切空間到 N 在 φ(x) 的切空間一個線性映射

$\mathrm {d} \varphi _{x}:T_{x}M\to T_{\varphi (x)}N\ ,$

映射 dφ_x 運用到切向量 X 上有時稱為 X 由 φ 的前推。前推的確切定義取決於我們怎樣定義切向量（不同的定義可參見切空間）。

如果我們定義切向量為通過 x 的曲線等價類，那麼微分由

$\mathrm {d} \varphi _{x}(\gamma '(0))=(\varphi \circ \gamma )'(0)$

給出，這裏 γ 是 M 上滿足 γ(0) = x 的一條曲線。換句話說，一條曲線 γ 在 0 處切向量的前推恰好是 φ$\circ$γ 在 0 處的切向量。

另一種方式，如果切向量定義為作用在光滑實值函數上的導子，那麼微分由

$\mathrm {d} \varphi _{x}(X)(f)=X(f\circ \varphi )$

給出，這裏 X ∈ T_xM，從而 X 是定義在 M 上的一個導子而 f 是 N 上一個光滑實值函數。根據定義，在給定 M 上 x 處 X 的前推在 T_φ(x)N 中，從而定義了一個N上的導子。

取定 x 與 φ(x) 附近的坐標卡以後，F 局部由 R^m 與 Rⁿ 之間的光滑映射

${\hat {\varphi }}:U\rightarrow V$

確定。而 dφ_x 具有表示（在 x 附近）：

$\mathrm {d} \varphi _{x}{\Bigl (}{\frac {\partial }{\partial u^{a}}}{\Bigr )}={\frac {\partial {\hat {\varphi }}^{b}}{\partial u^{a}}}{\frac {\partial }{\partial v^{b}}},$

這裏使用了愛因斯坦求和約定，偏導數對 x 坐標卡相應的 U 中的點取值。

線性擴張得到如下矩陣

$(\mathrm {d} \varphi _{x})_{a}^{\;b}={\frac {\partial {\hat {\varphi }}^{b}}{\partial u^{a}}}.$

從而光滑映射 φ 在每一點的微分是切空間之間的一個線性變換。從而在某些選定的局部坐標下，它表示為相應的從 R^m 到 Rⁿ 光滑映射的雅可比矩陣。一般情形，微分不要求可逆。如果 φ 是一個局部微分同胚，那麼在 x 點的前推是可逆的，其逆給出 T_φ(x)N 的拉回。

另外，局部微分同胚的微分是切空間之間的線性同構。

微分經常有其他一些記法，比如

$D\varphi _{x},\;(\varphi _{*})_{x},\;\varphi '(x)\ .$

從定義可得出複合函數的微分便是微分的複合（即，具有函子性質），這便是光滑函數微分的鏈式法則。

切叢上的微分

光滑映射 φ 的微分以顯而易見的方式誘導了從 M 的切叢到 N 的切叢的一個叢映射（事實上是向量叢同態），記為 dφ 或 φ_*，滿足如下的交換圖表：

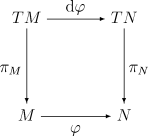
這裏 π_M 與 π_N 分別表示 M 與 N 切叢的叢投影。

等價地（參見叢映射），φ_* = dφ 是從 TM 到 M 上的拉回叢 φ^*TN 的叢映射，這可以看成 M 上向量叢 Hom(TM,φ^*TN) 的一個截面。

向量場的前推

給定了一個光滑映射 φ:M→N 與 M 上一個向量場 X，一般不能定義 X 通過 φ 的前推為 N 的一個向量場。譬如，如果映射 φ 不是滿射，則在 φ 的像外部沒有自然的方式定義拉回；如果 φ 不是單射也有可能在給定一點拉回不止一種選擇。無論如何，可以用「沿着映射的向量場」概念將難處變精確。

M 上 φ^*TN 的一個截面稱為沿着 φ 的向量場。例如，如果 M 是 N 的一個子叢而 φ 是包含映射，那麼沿着 φ 的向量場恰好是 N 沿着 M 的切叢的一個截面；特別的，M 上的向量通過 TM 包含到 TN 中定義這樣一個截面。這種想法推廣到任何光滑映射。

假設 X 是 M 上一個向量場，即 TM 的一個截面。那麼，運用逐點微分得出 X 的前推 φ_*X，這是一個沿着 φ 的向量場，即 M 上 φ^*TN 的一個截面。

任何 N 上的向量場 Y 定義了 φ^*TN 的一個拉回截面 φ^*Y 使得 (φ^*Y)_x = Y_φ(x)。M 上一個向量場 X 與 N 上一個向量場 Y 稱為 φ-相關的，如果作為沿着 φ 的向量場有 φ_*X = φ^*Y。換句話說，對任何 x 屬於 M，有 dφ_x(X)=Y_φ(x)。

在某些情形，給定 M 上一個向量場 X，N 上只有惟一的向量場 Y 與 X φ-相關。特別地，這在 φ 是微分同胚時自然成立。在這種情況下，前推定義了 N 上一個向量場 Y，由

$Y_{x}=\varphi _{*}(X_{\varphi ^{-1}(x)}).$

給出。一個更一般的情形是 φ 為滿射（比如纖維叢的叢投影）。這時 M 上的向量場 X 稱為可投影的，如果對任何 y 屬於 N, dφ_x(X_x) 與 x 屬於 φ^-1({y}) 的取法無關。這恰好是保證 X 的前推可以作為 N 上的一個良定的向量場的條件。

參閲

• 拉回

參考文獻

• John M. Lee, Introduction to Smooth Manifolds, (2003) Springer Graduate Texts in Mathematics 218.
• Jurgen Jost, Riemannian Geometry and Geometric Analysis, (2002) Springer-Verlag, Berlin ISBN 3-540-42627-2 See section 1.6.
• Ralph Abraham and Jerrold E. Marsden, Foundations of Mechanics, (1978) Benjamin-Cummings, London ISBN 0-8053-0102-X See section 1.7 and 2.3.