在数学 中,以法国 数学家 埃德蒙·拉盖尔 拉盖尔多项式 定义为拉盖尔方程 的标准解。
x
y
″
+
(
1
−
x
)
y
′
+
n
y
=
0
{\displaystyle x\,y''+(1-x)\,y'+n\,y=0\,}
这是一个二阶线性微分方程 。
这个方程只有当n 非负时,才有非奇异解。拉盖尔多项式可用在高斯积分法 中,计算形如
∫
0
∞
f
(
x
)
d
x
{\displaystyle \int _{0}^{\infty }f(x)dx}
这些多项式(通常用L 0 , L 1 等表示)构成一个多项式序列 罗德里格公式 递推得到。
L
n
(
x
)
=
e
x
n
!
d
n
d
x
n
(
e
−
x
x
n
)
.
{\displaystyle L_{n}(x)={\frac {e^{x}}{n!}}{\frac {d^{n}}{dx^{n}}}\left(e^{-x}x^{n}\right).}
在按照下式定义的内积构成的内积空间 中,拉盖尔多项式是正交多项式 。
⟨
f
,
g
⟩
=
∫
0
∞
f
(
x
)
g
(
x
)
e
−
x
d
x
.
{\displaystyle \langle f,g\rangle =\int _{0}^{\infty }f(x)g(x)e^{-x}\,dx.}
拉盖尔多项式构成一个Sheffer序列
拉盖尔多项式在量子力学中有重要应用。氢原子薛定谔方程 的解的径向部分,就是拉盖尔多项式。
物理学家通常采用另外一种拉盖尔多项式的定义形式,即在上面的形式的基础上乘上一个n !。
前几个拉盖尔多项式 [ 编辑 ] 前几个拉盖尔多项式的表达式与函数图像如下:
n
L
n
(
x
)
{\displaystyle L_{n}(x)\,}
0
1
{\displaystyle 1\,}
1
−
x
+
1
{\displaystyle -x+1\,}
2
1
2
(
x
2
−
4
x
+
2
)
{\displaystyle {\scriptstyle {\frac {1}{2}}}(x^{2}-4x+2)\,}
3
1
6
(
−
x
3
+
9
x
2
−
18
x
+
6
)
{\displaystyle {\scriptstyle {\frac {1}{6}}}(-x^{3}+9x^{2}-18x+6)\,}
4
1
24
(
x
4
−
16
x
3
+
72
x
2
−
96
x
+
24
)
{\displaystyle {\scriptstyle {\frac {1}{24}}}(x^{4}-16x^{3}+72x^{2}-96x+24)\,}
5
1
120
(
−
x
5
+
25
x
4
−
200
x
3
+
600
x
2
−
600
x
+
120
)
{\displaystyle {\scriptstyle {\frac {1}{120}}}(-x^{5}+25x^{4}-200x^{3}+600x^{2}-600x+120)\,}
6
1
720
(
x
6
−
36
x
5
+
450
x
4
−
2400
x
3
+
5400
x
2
−
4320
x
+
720
)
{\displaystyle {\scriptstyle {\frac {1}{720}}}(x^{6}-36x^{5}+450x^{4}-2400x^{3}+5400x^{2}-4320x+720)\,}
前六个拉盖尔多项式 递归定义 [ 编辑 ] 拉盖尔多项式也可以通过递归的方式进行定义。首先,规定前两个拉盖尔多项式为:
L
0
(
x
)
=
1
{\displaystyle L_{0}(x)=1\,}
L
1
(
x
)
=
1
−
x
{\displaystyle L_{1}(x)=1-x\,}
然后运用下面的递推关系 得到更高阶的多项式。
L
k
+
1
(
x
)
=
1
k
+
1
(
(
2
k
+
1
−
x
)
L
k
(
x
)
−
k
L
k
−
1
(
x
)
)
.
{\displaystyle L_{k+1}(x)={\frac {1}{k+1}}\left((2k+1-x)L_{k}(x)-kL_{k-1}(x)\right).}
广义拉盖尔多项式 [ 编辑 ] 上面提到的拉盖尔多项式的正交性,也可以用另外一种方式表达。即:如果X 是一个服从指数分布 的随机变量 (即,概率密度函数 如下式):
f
(
x
)
=
{
e
−
x
if
x
>
0
,
0
if
x
<
0
,
{\displaystyle f(x)=\left\{{\begin{matrix}e^{-x}&{\mbox{if}}\ x>0,\\0&{\mbox{if}}\ x<0,\end{matrix}}\right.}
那么:
E
[
L
n
(
X
)
L
m
(
X
)
]
=
0
whenever
n
≠
m
.
{\displaystyle E\left[L_{n}(X)L_{m}(X)\right]=0\ {\mbox{whenever}}\ n\neq m.}
指数分布不是唯一的伽玛分布 ,对于任意的伽玛分布(概率密度函数如下,α > −1,参见Γ函数 )
f
(
x
)
=
{
x
α
e
−
x
/
Γ
(
1
+
α
)
if
x
>
0
,
0
if
x
<
0
,
{\displaystyle f(x)=\left\{{\begin{matrix}x^{\alpha }e^{-x}/\Gamma (1+\alpha )&{\mbox{if}}\ x>0,\\0&{\mbox{if}}\ x<0,\end{matrix}}\right.}
相应的正交多项式为形如下式的广义拉盖尔多项式 (可以通过罗德里格公式 得到):
L
n
(
α
)
(
x
)
=
x
−
α
e
x
n
!
d
n
d
x
n
(
e
−
x
x
n
+
α
)
.
{\displaystyle L_{n}^{(\alpha )}(x)={x^{-\alpha }e^{x} \over n!}{d^{n} \over dx^{n}}\left(e^{-x}x^{n+\alpha }\right).}
有时也将上面的多项式称为连带(联属,伴随)拉盖尔多项式 。当取α = 0时,就回到拉盖尔多项式:
L
n
(
0
)
(
x
)
=
L
n
(
x
)
.
{\displaystyle L_{n}^{(0)}(x)=L_{n}(x).}
广义拉盖尔多项式的性质与应用 [ 编辑 ] 拉盖尔函数可以由合流超几何函数 和Kummer变换得到:
L
n
(
α
)
(
x
)
:=
(
n
+
α
n
)
M
(
−
n
,
α
+
1
,
x
)
=
(
n
+
α
n
)
∑
i
=
0
(
−
1
)
i
(
n
i
)
(
α
+
i
i
)
x
i
{\displaystyle L_{n}^{(\alpha )}(x):={n+\alpha \choose n}M(-n,\alpha +1,x)={n+\alpha \choose n}\sum _{i=0}(-1)^{i}{\frac {n \choose i}{\alpha +i \choose i}}x^{i}\,}
=
e
x
⋅
(
n
+
α
n
)
M
(
α
+
n
+
1
,
α
+
1
,
−
x
)
{\displaystyle =e^{x}\cdot {n+\alpha \choose n}M(\alpha +n+1,\alpha +1,-x)}
=
e
x
sin
(
n
π
)
sin
(
(
n
+
α
)
π
)
L
−
α
−
n
−
1
(
α
)
(
−
x
)
{\displaystyle ={\frac {e^{x}\sin(n\pi )}{\sin((n+\alpha )\pi )}}L_{-\alpha -n-1}^{(\alpha )}(-x)}
=
e
x
⋅
∑
i
=
0
(
−
1
)
i
(
α
+
n
+
i
n
)
x
i
i
!
.
{\displaystyle =e^{x}\cdot \sum _{i=0}(-1)^{i}{\alpha +n+i \choose n}{\frac {x^{i}}{i!}}.}
n
{\displaystyle n}
n
{\displaystyle n}
n
{\displaystyle n}
莱布尼茨乘积求导公式
L
n
(
α
)
(
x
)
=
∑
i
=
0
n
(
−
1
)
i
(
n
+
α
n
−
i
)
x
i
i
!
{\displaystyle L_{n}^{(\alpha )}(x)=\sum _{i=0}^{n}(-1)^{i}{n+\alpha \choose n-i}{\frac {x^{i}}{i!}}}
n 阶拉盖尔多项式的首项系数为(−1)n n !;拉盖尔多项式在x=0的取值(常数项 )为
L
n
(
α
)
(
0
)
=
(
n
+
α
n
)
≈
n
α
Γ
(
α
+
1
)
;
{\displaystyle L_{n}^{(\alpha )}(0)={n+\alpha \choose n}\approx {\frac {n^{\alpha }}{\Gamma (\alpha +1)}};}
L n (α ) 有n 个实 的正根 (应该注意到
(
(
−
1
)
n
−
i
L
n
−
i
(
α
)
)
i
=
0
n
{\displaystyle \left((-1)^{n-i}L_{n-i}^{(\alpha )}\right)_{i=0}^{n}}
施图姆序列 ),且这些根全部位于区间
(
0
,
n
+
α
+
(
n
−
1
)
n
+
α
]
{\displaystyle (0,n+\alpha +(n-1){\sqrt {n+\alpha }}]}
当
n
{\displaystyle n}
α
{\displaystyle \alpha }
x
>
0
{\displaystyle x>0}
L
n
(
α
)
(
x
)
≈
n
α
2
−
1
4
π
e
x
2
x
α
2
+
1
4
cos
(
2
x
(
n
+
α
+
1
2
)
−
π
2
(
α
+
1
2
)
)
{\displaystyle L_{n}^{(\alpha )}(x)\approx {\frac {n^{{\frac {\alpha }{2}}-{\frac {1}{4}}}}{\sqrt {\pi }}}{\frac {e^{\frac {x}{2}}}{x^{{\frac {\alpha }{2}}+{\frac {1}{4}}}}}\cos \left(2{\sqrt {x\left(n+{\frac {\alpha +1}{2}}\right)}}-{\frac {\pi }{2}}\left(\alpha +{\frac {1}{2}}\right)\right)}
L
n
(
α
)
(
−
x
)
≈
n
α
2
−
1
4
2
π
e
−
x
2
x
α
2
+
1
4
exp
(
2
x
(
n
+
α
+
1
2
)
)
{\displaystyle L_{n}^{(\alpha )}(-x)\approx {\frac {n^{{\frac {\alpha }{2}}-{\frac {1}{4}}}}{2{\sqrt {\pi }}}}{\frac {e^{-{\frac {x}{2}}}}{x^{{\frac {\alpha }{2}}+{\frac {1}{4}}}}}\exp \left(2{\sqrt {x\left(n+{\frac {\alpha +1}{2}}\right)}}\right)}
[1]
L
0
(
α
)
(
x
)
=
1
{\displaystyle L_{0}^{(\alpha )}(x)=1}
L
1
(
α
)
(
x
)
=
−
x
+
α
+
1
{\displaystyle L_{1}^{(\alpha )}(x)=-x+\alpha +1}
L
2
(
α
)
(
x
)
=
x
2
2
−
(
α
+
2
)
x
+
(
α
+
2
)
(
α
+
1
)
2
{\displaystyle L_{2}^{(\alpha )}(x)={\frac {x^{2}}{2}}-(\alpha +2)x+{\frac {(\alpha +2)(\alpha +1)}{2}}}
L
3
(
α
)
(
x
)
=
−
x
3
6
+
(
α
+
3
)
x
2
2
−
(
α
+
2
)
(
α
+
3
)
x
2
+
(
α
+
1
)
(
α
+
2
)
(
α
+
3
)
6
{\displaystyle L_{3}^{(\alpha )}(x)={\frac {-x^{3}}{6}}+{\frac {(\alpha +3)x^{2}}{2}}-{\frac {(\alpha +2)(\alpha +3)x}{2}}+{\frac {(\alpha +1)(\alpha +2)(\alpha +3)}{6}}}
根据拉盖尔多项式的定义,可以使用秦九韶算法 计算拉盖尔多项式,程序代码如下: function LaguerreL(n, alpha, x) {
LaguerreL:= 1; bin:= 1
for i:= n to 1 step -1 {
bin:= bin* (alpha+ i)/ (n+ 1- i)
LaguerreL:= bin- x* LaguerreL/ i
}
return LaguerreL;
}
递推关系 [ 编辑 ] 拉盖尔多项式满足以下的递推关系:
L
n
(
α
+
β
+
1
)
(
x
+
y
)
=
∑
i
=
0
n
L
i
(
α
)
(
x
)
L
n
−
i
(
β
)
(
y
)
,
{\displaystyle L_{n}^{(\alpha +\beta +1)}(x+y)=\sum _{i=0}^{n}L_{i}^{(\alpha )}(x)L_{n-i}^{(\beta )}(y),}
特别地,有
L
n
(
α
+
1
)
(
x
)
=
∑
i
=
0
n
L
i
(
α
)
(
x
)
{\displaystyle L_{n}^{(\alpha +1)}(x)=\sum _{i=0}^{n}L_{i}^{(\alpha )}(x)}
L
n
(
α
)
(
x
)
=
∑
i
=
0
n
(
α
−
β
+
n
−
i
−
1
n
−
i
)
L
i
(
β
)
(
x
)
{\displaystyle L_{n}^{(\alpha )}(x)=\sum _{i=0}^{n}{\alpha -\beta +n-i-1 \choose n-i}L_{i}^{(\beta )}(x)}
L
n
(
α
)
(
x
)
=
∑
i
=
0
n
(
α
−
β
+
n
n
−
i
)
L
i
(
β
−
i
)
(
x
)
;
{\displaystyle L_{n}^{(\alpha )}(x)=\sum _{i=0}^{n}{\alpha -\beta +n \choose n-i}L_{i}^{(\beta -i)}(x);}
还有
L
n
(
α
)
(
x
)
−
∑
j
=
0
Δ
−
1
(
n
+
α
n
−
j
)
(
−
1
)
j
x
j
j
!
=
(
−
1
)
Δ
x
Δ
(
Δ
−
1
)
!
∑
i
=
0
n
−
Δ
(
n
+
α
n
−
Δ
−
i
)
(
n
−
i
)
(
n
i
)
L
i
(
α
+
Δ
)
(
x
)
=
(
−
1
)
Δ
x
Δ
(
Δ
−
1
)
!
∑
i
=
0
n
−
Δ
(
n
+
α
−
i
−
1
n
−
Δ
−
i
)
(
n
−
i
)
(
n
i
)
L
i
(
n
+
α
+
Δ
−
i
)
(
x
)
.
{\displaystyle {\begin{aligned}L_{n}^{(\alpha )}(x)-\sum _{j=0}^{\Delta -1}{n+\alpha \choose n-j}(-1)^{j}{\frac {x^{j}}{j!}}&=(-1)^{\Delta }{\frac {x^{\Delta }}{(\Delta -1)!}}\sum _{i=0}^{n-\Delta }{\frac {n+\alpha \choose n-\Delta -i}{(n-i){n \choose i}}}L_{i}^{(\alpha +\Delta )}(x)\\&=(-1)^{\Delta }{\frac {x^{\Delta }}{(\Delta -1)!}}\sum _{i=0}^{n-\Delta }{\frac {n+\alpha -i-1 \choose n-\Delta -i}{(n-i){n \choose i}}}L_{i}^{(n+\alpha +\Delta -i)}(x).\end{aligned}}}
运用以上式子可以得到以下四条关系式:
L
n
(
α
)
(
x
)
=
L
n
(
α
+
1
)
(
x
)
−
L
n
−
1
(
α
+
1
)
(
x
)
{\displaystyle L_{n}^{(\alpha )}(x)=L_{n}^{(\alpha +1)}(x)-L_{n-1}^{(\alpha +1)}(x)}
=
∑
j
=
0
k
(
k
j
)
L
n
−
j
(
α
−
k
+
j
)
(
x
)
,
{\displaystyle =\sum _{j=0}^{k}{k \choose j}L_{n-j}^{(\alpha -k+j)}(x),}
n
L
n
(
α
)
(
x
)
=
(
n
+
α
)
L
n
−
1
(
α
)
(
x
)
−
x
L
n
−
1
(
α
+
1
)
(
x
)
,
{\displaystyle nL_{n}^{(\alpha )}(x)=(n+\alpha )L_{n-1}^{(\alpha )}(x)-xL_{n-1}^{(\alpha +1)}(x),}
x
k
k
!
L
n
(
α
)
(
x
)
=
∑
i
=
0
k
(
−
1
)
i
(
n
+
i
i
)
(
n
+
α
k
−
i
)
L
n
+
i
(
α
−
k
)
(
x
)
,
{\displaystyle {\frac {x^{k}}{k!}}L_{n}^{(\alpha )}(x)=\sum _{i=0}^{k}(-1)^{i}{n+i \choose i}{n+\alpha \choose k-i}L_{n+i}^{(\alpha -k)}(x),}
n
L
n
(
α
+
1
)
(
x
)
=
(
n
−
x
)
L
n
−
1
(
α
+
1
)
(
x
)
+
(
n
+
α
)
L
n
−
1
(
α
)
(
x
)
{\displaystyle nL_{n}^{(\alpha +1)}(x)=(n-x)L_{n-1}^{(\alpha +1)}(x)+(n+\alpha )L_{n-1}^{(\alpha )}(x)}
x
L
n
(
α
+
1
)
=
(
n
+
α
)
L
n
−
1
α
(
x
)
−
(
n
−
x
)
L
n
(
α
)
(
x
)
;
{\displaystyle xL_{n}^{(\alpha +1)}=(n+\alpha )L_{n-1}^{\alpha }(x)-(n-x)L_{n}^{(\alpha )}(x);}
将它们组合在一起,就得到了最常用的递推关系式:
L
n
+
1
(
α
)
(
x
)
=
1
n
+
1
(
(
2
n
+
1
+
α
−
x
)
L
n
(
α
)
(
x
)
−
(
n
+
α
)
L
n
−
1
(
α
)
(
x
)
)
.
{\displaystyle L_{n+1}^{(\alpha )}(x)={\frac {1}{n+1}}\left((2n+1+\alpha -x)L_{n}^{(\alpha )}(x)-(n+\alpha )L_{n-1}^{(\alpha )}(x)\right).}
当
i
{\displaystyle i}
n
{\displaystyle n}
(
−
x
)
i
i
!
L
n
(
i
−
n
)
(
x
)
=
(
−
x
)
n
n
!
L
i
(
n
−
i
)
(
x
)
;
{\displaystyle {\frac {(-x)^{i}}{i!}}L_{n}^{(i-n)}(x)={\frac {(-x)^{n}}{n!}}L_{i}^{(n-i)}(x);}
进一步可以得到部分分式分解 :
L
n
(
α
)
(
x
)
(
n
+
α
n
)
=
1
−
∑
j
=
1
n
x
j
α
+
j
L
n
−
j
(
j
)
(
x
)
(
j
−
1
)
!
=
1
−
x
∑
i
=
1
n
L
n
−
i
(
−
α
)
(
x
)
L
i
−
1
(
α
+
1
)
(
−
x
)
α
+
i
.
{\displaystyle {\frac {L_{n}^{(\alpha )}(x)}{n+\alpha \choose n}}=1-\sum _{j=1}^{n}{\frac {x^{j}}{\alpha +j}}{\frac {L_{n-j}^{(j)}(x)}{(j-1)!}}=1-x\sum _{i=1}^{n}{\frac {L_{n-i}^{(-\alpha )}(x)L_{i-1}^{(\alpha +1)}(-x)}{\alpha +i}}.}
拉盖尔多项式的导函数 [ 编辑 ] 将拉盖尔多项式对自变量x 求导k 次,得到:
d
k
d
x
k
L
n
(
α
)
(
x
)
=
(
−
1
)
k
L
n
−
k
(
α
+
k
)
(
x
)
;
{\displaystyle {\frac {\mathrm {d} ^{k}}{\mathrm {d} x^{k}}}L_{n}^{(\alpha )}(x)=(-1)^{k}L_{n-k}^{(\alpha +k)}(x)\,;}
进一步有:
1
k
!
d
k
d
x
k
x
α
L
n
(
α
)
(
x
)
=
(
n
+
α
k
)
x
α
−
k
L
n
(
α
−
k
)
(
x
)
,
{\displaystyle {\frac {1}{k!}}{\frac {\mathrm {d} ^{k}}{\mathrm {d} x^{k}}}x^{\alpha }L_{n}^{(\alpha )}(x)={n+\alpha \choose k}x^{\alpha -k}L_{n}^{(\alpha -k)}(x),}
运用柯西多重积分公式
L
n
(
α
′
)
(
x
)
=
(
α
′
−
α
)
(
α
′
+
n
α
′
−
α
)
∫
0
x
t
α
(
x
−
t
)
α
′
−
α
−
1
x
α
′
L
n
(
α
)
(
t
)
d
t
.
{\displaystyle L_{n}^{(\alpha ')}(x)=(\alpha '-\alpha ){\alpha '+n \choose \alpha '-\alpha }\int _{0}^{x}{\frac {t^{\alpha }(x-t)^{\alpha '-\alpha -1}}{x^{\alpha '}}}L_{n}^{(\alpha )}(t)\,dt.}
将拉盖尔多项式对参变量
α
{\displaystyle \alpha }
d
d
α
L
n
(
α
)
(
x
)
=
∑
i
=
0
n
−
1
L
i
(
α
)
(
x
)
n
−
i
.
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} \alpha }}L_{n}^{(\alpha )}(x)=\sum _{i=0}^{n-1}{\frac {L_{i}^{(\alpha )}(x)}{n-i}}.}
广义拉盖尔多项式满足下面的微分方程:
x
L
n
(
α
)
′
′
(
x
)
+
(
α
+
1
−
x
)
L
n
(
α
)
′
(
x
)
+
n
L
n
(
α
)
(
x
)
=
0
,
{\displaystyle xL_{n}^{(\alpha )\prime \prime }(x)+(\alpha +1-x)L_{n}^{(\alpha )\prime }(x)+nL_{n}^{(\alpha )}(x)=0,\,}
可以与拉盖尔多项式的k阶导数所满足的微分方程作一比较。
x
L
n
(
k
)
′
′
(
x
)
+
(
k
+
1
−
x
)
L
n
(
k
)
′
(
x
)
+
(
n
−
k
)
L
n
(
k
)
(
x
)
=
0
,
{\displaystyle xL_{n}^{(k)\prime \prime }(x)+(k+1-x)L_{n}^{(k)\prime }(x)+(n-k)L_{n}^{(k)}(x)=0,\,}
仅在此式中,
L
n
(
k
)
(
x
)
≡
d
L
n
(
x
)
d
x
k
{\displaystyle L_{n}^{(k)}(x)\equiv {\frac {dL_{n}(x)}{dx^{k}}}}
于是,当
α
=
0
{\displaystyle \alpha =0}
L
n
(
k
)
(
x
)
=
(
−
1
)
k
d
L
n
+
k
(
x
)
d
x
k
{\displaystyle L_{n}^{(k)}(x)=(-1)^{k}{\frac {dL_{n+k}(x)}{dx^{k}}}}
正交性 [ 编辑 ] 伴随拉盖尔多项式在区间[0, ∞)上以权函数x α e −x 正交:
∫
0
∞
x
α
e
−
x
L
n
(
α
)
(
x
)
L
m
(
α
)
(
x
)
d
x
=
Γ
(
n
+
α
+
1
)
n
!
δ
n
,
m
,
{\displaystyle \int _{0}^{\infty }x^{\alpha }e^{-x}L_{n}^{(\alpha )}(x)L_{m}^{(\alpha )}(x)dx={\frac {\Gamma (n+\alpha +1)}{n!}}\delta _{n,m},}
这可由下式得到:
∫
0
∞
x
α
′
−
1
e
−
x
L
n
(
α
)
(
x
)
d
x
=
(
α
−
α
′
+
n
n
)
Γ
(
α
′
)
.
{\displaystyle \int _{0}^{\infty }x^{\alpha '-1}e^{-x}L_{n}^{(\alpha )}(x)dx={\alpha -\alpha '+n \choose n}\Gamma (\alpha ').}
伴随对称核多项式可以用拉盖尔多项式表示为:
K
n
(
α
)
(
x
,
y
)
:=
1
Γ
(
α
+
1
)
∑
i
=
0
n
L
i
(
α
)
(
x
)
L
i
(
α
)
(
y
)
(
α
+
i
i
)
=
1
Γ
(
α
+
1
)
L
n
(
α
)
(
x
)
L
n
+
1
(
α
)
(
y
)
−
L
n
+
1
(
α
)
(
x
)
L
n
(
α
)
(
y
)
x
−
y
n
+
1
(
n
+
α
n
)
=
1
Γ
(
α
+
1
)
∑
i
=
0
n
x
i
i
!
L
n
−
i
(
α
+
i
)
(
x
)
L
n
−
i
(
α
+
i
+
1
)
(
y
)
(
α
+
n
n
)
(
n
i
)
;
{\displaystyle {\begin{aligned}K_{n}^{(\alpha )}(x,y)&{:=}{\frac {1}{\Gamma (\alpha +1)}}\sum _{i=0}^{n}{\frac {L_{i}^{(\alpha )}(x)L_{i}^{(\alpha )}(y)}{\alpha +i \choose i}}\\&{=}{\frac {1}{\Gamma (\alpha +1)}}{\frac {L_{n}^{(\alpha )}(x)L_{n+1}^{(\alpha )}(y)-L_{n+1}^{(\alpha )}(x)L_{n}^{(\alpha )}(y)}{{\frac {x-y}{n+1}}{n+\alpha \choose n}}}\\&{=}{\frac {1}{\Gamma (\alpha +1)}}\sum _{i=0}^{n}{\frac {x^{i}}{i!}}{\frac {L_{n-i}^{(\alpha +i)}(x)L_{n-i}^{(\alpha +i+1)}(y)}{{\alpha +n \choose n}{n \choose i}}};\end{aligned}}}
也有下面的递推关系:
K
n
(
α
)
(
x
,
y
)
=
y
α
+
1
K
n
−
1
(
α
+
1
)
(
x
,
y
)
+
1
Γ
(
α
+
1
)
L
n
(
α
+
1
)
(
x
)
L
n
(
α
)
(
y
)
(
α
+
n
n
)
.
{\displaystyle K_{n}^{(\alpha )}(x,y)={\frac {y}{\alpha +1}}K_{n-1}^{(\alpha +1)}(x,y)+{\frac {1}{\Gamma (\alpha +1)}}{\frac {L_{n}^{(\alpha +1)}(x)L_{n}^{(\alpha )}(y)}{\alpha +n \choose n}}.}
进一步地,在伴L 2 [0, ∞)空间上,有:
y
α
e
−
y
K
n
(
α
)
(
⋅
,
y
)
→
δ
(
y
−
⋅
)
,
{\displaystyle y^{\alpha }e^{-y}K_{n}^{(\alpha )}(\cdot ,y)\rightarrow \delta (y-\,\cdot ),}
在氢原子的量子力学处理中用到了下面的公式:
∫
0
∞
x
α
+
1
e
−
x
[
L
n
(
α
)
]
2
d
x
=
(
n
+
α
)
!
n
!
(
2
n
+
α
+
1
)
.
{\displaystyle \int _{0}^{\infty }x^{\alpha +1}e^{-x}\left[L_{n}^{(\alpha )}\right]^{2}dx={\frac {(n+\alpha )!}{n!}}(2n+\alpha +1).}
级数展开 [ 编辑 ] 设一个函数具有以下的级数展开形式:
f
(
x
)
=
∑
i
=
0
f
i
(
α
)
L
i
(
α
)
(
x
)
.
{\displaystyle f(x)=\sum _{i=0}f_{i}^{(\alpha )}L_{i}^{(\alpha )}(x).}
则展开式的系数由下式给出
f
i
(
α
)
=
∫
0
∞
L
i
(
α
)
(
x
)
(
i
+
α
i
)
⋅
x
α
e
−
x
Γ
(
α
+
1
)
⋅
f
(
x
)
d
x
.
{\displaystyle f_{i}^{(\alpha )}=\int _{0}^{\infty }{\frac {L_{i}^{(\alpha )}(x)}{i+\alpha \choose i}}\cdot {\frac {x^{\alpha }e^{-x}}{\Gamma (\alpha +1)}}\cdot f(x)\,dx.}
这个级数在Lp空间
L
2
[
0
,
∞
)
{\displaystyle L^{2}[0,\infty )}
当且仅当
‖
f
‖
L
2
2
:=
∫
0
∞
x
α
e
−
x
Γ
(
α
+
1
)
|
f
(
x
)
|
2
d
x
=
∑
i
=
0
(
i
+
α
i
)
|
f
i
(
α
)
|
2
<
∞
.
{\displaystyle \|f\|_{L^{2}}^{2}:=\int _{0}^{\infty }{\frac {x^{\alpha }e^{-x}}{\Gamma (\alpha +1)}}|f(x)|^{2}dx=\sum _{i=0}{i+\alpha \choose i}|f_{i}^{(\alpha )}|^{2}<\infty .}
一个相关的展开式为:
f
(
x
)
=
e
γ
1
+
γ
x
⋅
∑
i
=
0
L
i
(
α
)
(
x
1
+
γ
)
(
1
+
γ
)
i
+
α
+
1
∑
n
=
0
i
γ
i
−
n
(
i
n
)
f
n
(
α
)
;
{\displaystyle f(x)=e^{{\frac {\gamma }{1+\gamma }}x}\cdot \sum _{i=0}{\frac {L_{i}^{(\alpha )}\left({\frac {x}{1+\gamma }}\right)}{(1+\gamma )^{i+\alpha +1}}}\sum _{n=0}^{i}\gamma ^{i-n}{i \choose n}f_{n}^{(\alpha )};}
特别地
e
−
γ
x
⋅
L
n
(
α
)
(
x
(
1
+
γ
)
)
=
∑
i
=
n
L
i
(
α
)
(
x
)
(
1
+
γ
)
i
+
α
+
1
γ
i
−
n
(
i
n
)
,
{\displaystyle e^{-\gamma x}\cdot L_{n}^{(\alpha )}(x(1+\gamma ))=\sum _{i=n}{\frac {L_{i}^{(\alpha )}(x)}{(1+\gamma )^{i+\alpha +1}}}\gamma ^{i-n}{i \choose n},}
这可由下式得到:
L
n
(
α
)
(
x
1
+
γ
)
=
1
(
1
+
γ
)
n
∑
i
=
0
n
γ
n
−
i
(
n
+
α
n
−
i
)
L
i
(
α
)
(
x
)
.
{\displaystyle L_{n}^{(\alpha )}\left({\frac {x}{1+\gamma }}\right)={\frac {1}{(1+\gamma )^{n}}}\sum _{i=0}^{n}\gamma ^{n-i}{n+\alpha \choose n-i}L_{i}^{(\alpha )}(x).}
还有,当
Re
(
2
α
−
β
)
>
−
1
{\displaystyle \operatorname {Re} {(2\alpha -\beta )}>-1}
x
α
−
β
f
(
x
)
Γ
(
α
−
β
+
1
)
=
(
α
β
)
∑
i
=
0
L
i
(
β
)
(
x
)
(
β
+
i
i
)
∑
n
=
0
i
(
−
1
)
i
−
n
(
α
−
β
i
−
n
)
(
α
+
n
n
)
f
n
(
α
)
,
{\displaystyle {\frac {x^{\alpha -\beta }f(x)}{\Gamma (\alpha -\beta +1)}}={\alpha \choose \beta }\sum _{i=0}{\frac {L_{i}^{(\beta )}(x)}{\beta +i \choose i}}\sum _{n=0}^{i}(-1)^{i-n}{\alpha -\beta \choose i-n}{\alpha +n \choose n}f_{n}^{(\alpha )},}
这个结果可以由下式导出,
x
α
−
β
L
n
(
α
)
(
x
)
Γ
(
α
−
β
+
1
)
=
(
α
β
)
(
α
+
n
n
)
∑
i
=
n
(
−
1
)
i
−
n
(
α
−
β
i
−
n
)
L
i
(
β
)
(
x
)
(
β
+
i
i
)
{\displaystyle {\frac {x^{\alpha -\beta }L_{n}^{(\alpha )}(x)}{\Gamma (\alpha -\beta +1)}}={\alpha \choose \beta }{\alpha +n \choose n}\sum _{i=n}(-1)^{i-n}{\alpha -\beta \choose i-n}{\frac {L_{i}^{(\beta )}(x)}{\beta +i \choose i}}}
更多的例子 [ 编辑 ] 幂函数 可以展开为:
x
n
n
!
=
∑
i
=
0
n
(
−
1
)
i
(
n
+
α
n
−
i
)
L
i
(
α
)
(
x
)
=
(
−
1
)
n
∑
i
=
0
n
L
i
(
α
−
i
)
(
x
)
(
−
α
n
−
i
)
,
{\displaystyle {\frac {x^{n}}{n!}}=\sum _{i=0}^{n}(-1)^{i}{n+\alpha \choose n-i}L_{i}^{(\alpha )}(x)=(-1)^{n}\sum _{i=0}^{n}L_{i}^{(\alpha -i)}(x){-\alpha \choose n-i},}
二项式 可以展开为:
(
n
+
x
n
)
=
∑
i
=
0
n
α
i
i
!
L
n
−
i
(
x
+
i
)
(
α
)
.
{\displaystyle {n+x \choose n}=\sum _{i=0}^{n}{\frac {\alpha ^{i}}{i!}}L_{n-i}^{(x+i)}(\alpha ).}
进一步可以得到:
e
−
γ
x
=
∑
i
=
0
γ
i
(
1
+
γ
)
i
+
α
+
1
L
i
(
α
)
(
x
)
{\displaystyle e^{-\gamma x}=\sum _{i=0}{\frac {\gamma ^{i}}{(1+\gamma )^{i+\alpha +1}}}L_{i}^{(\alpha )}(x)}
Re
(
γ
)
>
−
1
2
{\displaystyle \operatorname {Re} {(\gamma )}>-{\frac {1}{2}}}
更一般地
x
β
e
−
γ
x
Γ
(
β
+
1
)
=
(
α
+
β
α
)
∑
i
=
0
L
i
(
α
)
(
x
)
(
α
+
i
i
)
∑
j
=
0
i
(
−
1
)
j
(
1
+
γ
)
α
+
β
+
j
+
1
(
α
+
β
+
j
j
)
(
α
+
i
i
−
j
)
.
{\displaystyle {\frac {x^{\beta }e^{-\gamma x}}{\Gamma (\beta +1)}}={\alpha +\beta \choose \alpha }\sum _{i=0}{\frac {L_{i}^{(\alpha )}(x)}{\alpha +i \choose i}}\sum _{j=0}^{i}{\frac {(-1)^{j}}{(1+\gamma )^{\alpha +\beta +j+1}}}{\alpha +\beta +j \choose j}{\alpha +i \choose i-j}.}
对于非负的整数
β
{\displaystyle \beta }
x
n
e
−
γ
x
n
!
=
∑
i
=
0
γ
i
L
i
(
α
)
(
x
)
(
1
+
γ
)
i
+
n
+
α
+
1
∑
j
=
0
n
(
−
1
)
n
−
j
γ
j
(
n
+
α
j
)
(
i
n
−
j
)
,
{\displaystyle {\frac {x^{n}e^{-\gamma x}}{n!}}=\sum _{i=0}{\frac {\gamma ^{i}L_{i}^{(\alpha )}(x)}{(1+\gamma )^{i+n+\alpha +1}}}\sum _{j=0}^{n}(-1)^{n-j}\gamma ^{j}{n+\alpha \choose j}{i \choose n-j},}
当
γ
=
0
{\displaystyle \gamma =0}
x
β
Γ
(
β
+
1
)
=
(
α
+
β
α
)
∑
i
=
0
(
−
1
)
i
(
β
i
)
L
i
(
α
)
(
x
)
(
α
+
i
i
)
,
{\displaystyle {\frac {x^{\beta }}{\Gamma (\beta +1)}}={\alpha +\beta \choose \alpha }\sum _{i=0}(-1)^{i}{\beta \choose i}{\frac {L_{i}^{(\alpha )}(x)}{\alpha +i \choose i}},}
x
β
L
n
(
γ
)
(
x
)
Γ
(
β
+
1
)
=
(
α
+
β
α
)
∑
i
=
0
L
i
(
α
)
(
x
)
(
α
+
i
i
)
∑
j
=
0
n
(
−
1
)
i
−
j
(
n
+
γ
n
−
j
)
(
β
+
j
i
)
(
α
+
β
+
j
j
)
.
{\displaystyle {\frac {x^{\beta }L_{n}^{(\gamma )}(x)}{\Gamma (\beta +1)}}={\alpha +\beta \choose \alpha }\sum _{i=0}{\frac {L_{i}^{(\alpha )}(x)}{\alpha +i \choose i}}\sum _{j=0}^{n}(-1)^{i-j}{n+\gamma \choose n-j}{\beta +j \choose i}{\alpha +\beta +j \choose j}.}
雅可比Theta 函数 有下面的表示:
∑
k
∈
Z
e
−
k
2
π
x
=
∑
i
=
0
L
i
(
α
)
(
x
t
)
∑
k
∈
Z
(
k
2
π
t
)
i
(
1
+
k
2
π
t
)
i
+
α
+
1
;
{\displaystyle \sum _{k\in \mathbb {Z} }e^{-k^{2}\pi x}=\sum _{i=0}L_{i}^{(\alpha )}\left({\frac {x}{t}}\right)\sum _{k\in \mathbb {Z} }{\frac {(k^{2}\pi t)^{i}}{(1+k^{2}\pi t)^{i+\alpha +1}}};}
随意选定参量t,贝塞尔函数 可以表示为:
J
α
(
x
)
(
x
2
)
α
=
e
−
t
Γ
(
α
+
1
)
∑
i
=
0
L
i
(
α
)
(
x
2
4
t
)
(
i
+
α
i
)
t
i
i
!
;
{\displaystyle {\frac {J_{\alpha }(x)}{\left({\frac {x}{2}}\right)^{\alpha }}}={\frac {e^{-t}}{\Gamma (\alpha +1)}}\sum _{i=0}{\frac {L_{i}^{(\alpha )}\left({\frac {x^{2}}{4t}}\right)}{i+\alpha \choose i}}{\frac {t^{i}}{i!}};}
Γ函数 可以展开为:
Γ
(
α
)
=
x
α
∑
i
=
0
L
i
(
α
)
(
x
)
α
+
i
(
ℜ
(
α
)
<
1
2
)
;
{\displaystyle \Gamma (\alpha )=x^{\alpha }\sum _{i=0}{\frac {L_{i}^{(\alpha )}(x)}{\alpha +i}}\qquad \left(\Re (\alpha )<{\frac {1}{2}}\right);}
低阶不完全伽玛函数 可展开为:
γ
(
s
;
z
)
t
s
Γ
(
s
)
=
(
z
t
)
α
Γ
(
α
+
1
)
∑
i
=
0
L
i
(
α
)
(
z
t
)
(
α
+
i
i
)
∑
j
=
0
i
(
−
1
)
j
(
1
+
t
)
s
+
j
(
s
−
1
+
j
j
)
(
α
−
1
+
i
i
−
j
)
,
{\displaystyle {\frac {\gamma (s;z)}{t^{s}\Gamma (s)}}={\frac {\left({\frac {z}{t}}\right)^{\alpha }}{\Gamma (\alpha +1)}}\sum _{i=0}{\frac {L_{i}^{(\alpha )}\left({\frac {z}{t}}\right)}{\alpha +i \choose i}}\sum _{j=0}^{i}{\frac {(-1)^{j}}{(1+t)^{s+j}}}{s-1+j \choose j}{\alpha -1+i \choose i-j},}
γ
(
s
;
z
)
t
s
Γ
(
s
)
=
(
α
+
s
α
+
1
)
∑
i
=
0
(
α
+
i
+
1
i
+
1
)
−
L
i
+
1
(
α
)
(
z
t
)
(
α
+
i
+
1
i
)
∑
j
=
0
i
(
−
1
)
j
(
1
+
t
)
α
+
1
+
s
+
j
(
α
+
s
+
j
j
)
(
α
+
i
+
1
i
−
j
)
.
{\displaystyle {\frac {\gamma (s;z)}{t^{s}\Gamma (s)}}={\alpha +s \choose \alpha +1}\sum _{i=0}{\frac {{\alpha +i+1 \choose i+1}-L_{i+1}^{(\alpha )}\left({\frac {z}{t}}\right)}{\alpha +i+1 \choose i}}\sum _{j=0}^{i}{\frac {(-1)^{j}}{(1+t)^{\alpha +1+s+j}}}{\alpha +s+j \choose j}{\alpha +i+1 \choose i-j}.}
还有:
γ
(
s
,
z
)
=
γ
s
Γ
(
1
−
s
)
∑
i
=
0
L
i
+
1
(
−
s
)
(
0
)
−
L
i
+
1
(
−
s
)
(
z
γ
)
(
1
+
γ
)
i
+
1
∑
n
=
0
i
γ
i
−
n
(
i
n
)
n
+
1
−
s
;
{\displaystyle \gamma (s,z)={\frac {\gamma ^{s}}{\Gamma (1-s)}}\sum _{i=0}{\frac {L_{i+1}^{(-s)}(0)-L_{i+1}^{(-s)}\left({\frac {z}{\gamma }}\right)}{(1+\gamma )^{i+1}}}\sum _{n=0}^{i}\gamma ^{i-n}{\frac {i \choose n}{n+1-s}};}
于是,高阶不完全伽玛函数就是:
Γ
(
s
,
z
)
z
s
e
−
z
=
∑
k
=
0
L
k
(
α
)
(
z
)
(
k
+
1
)
(
k
+
1
+
α
−
s
k
+
1
)
(
ℜ
(
s
−
α
2
)
<
1
4
)
=
∑
k
=
0
L
k
(
α
)
(
z
t
)
⋅
2
F
1
(
1
+
α
+
k
,
1
+
k
;
2
+
α
+
k
−
s
;
t
−
1
t
)
t
k
(
k
+
1
)
(
1
+
α
+
k
−
s
1
+
k
)
=
t
s
∑
k
=
0
L
k
(
α
)
(
z
t
)
⋅
2
F
1
(
1
−
s
,
1
+
α
−
s
;
2
+
α
+
k
−
s
;
t
−
1
t
)
(
k
+
1
)
(
1
+
α
+
k
−
s
1
+
k
)
=
t
1
+
α
∑
k
=
0
L
k
(
α
)
(
z
t
)
⋅
2
F
1
(
1
+
α
+
k
,
1
+
α
−
s
;
2
+
α
+
k
−
s
;
1
−
t
)
(
k
+
1
)
(
1
+
α
+
k
−
s
1
+
k
)
,
{\displaystyle {\begin{aligned}{\frac {\Gamma (s,z)}{z^{s}e^{-z}}}&=\sum _{k=0}{\frac {L_{k}^{(\alpha )}(z)}{(k+1){k+1+\alpha -s \choose k+1}}}\qquad \left(\Re \left(s-{\frac {\alpha }{2}}\right)<{\frac {1}{4}}\right)\\&=\sum _{k=0}L_{k}^{(\alpha )}(z\,t)\cdot {\frac {_{2}F_{1}\left(1+\alpha +k,1+k;2+\alpha +k-s;{\frac {t-1}{t}}\right)}{t^{k}(k+1){1+\alpha +k-s \choose 1+k}}}\\&=t^{s}\sum _{k=0}L_{k}^{(\alpha )}(z\,t)\cdot {\frac {_{2}F_{1}\left(1-s,1+\alpha -s;2+\alpha +k-s;{\frac {t-1}{t}}\right)}{(k+1){1+\alpha +k-s \choose 1+k}}}\\&=t^{1+\alpha }\sum _{k=0}L_{k}^{(\alpha )}(z\,t)\cdot {\frac {_{2}F_{1}\left(1+\alpha +k,1+\alpha -s;2+\alpha +k-s;1-t\right)}{(k+1){1+\alpha +k-s \choose 1+k}}},\end{aligned}}}
2
F
1
{\displaystyle _{2}F_{1}}
超几何函数 。
围道积分表示 [ 编辑 ] 拉盖尔多项式可以用围道积分 表示,如下式所示:
L
n
(
α
)
(
x
)
=
1
2
π
i
∮
e
−
x
t
1
−
t
(
1
−
t
)
α
+
1
t
n
+
1
d
t
{\displaystyle L_{n}^{(\alpha )}(x)={\frac {1}{2\pi i}}\oint {\frac {e^{-{\frac {xt}{1-t}}}}{(1-t)^{\alpha +1}\,t^{n+1}}}\;dt}
积分方向逆时针绕原点一周。
与埃爾米特多項式的关系 [ 编辑 ] 广义拉盖尔多项式与埃爾米特多項式有下列关系:
H
2
n
(
x
)
=
(
−
1
)
n
2
2
n
n
!
L
n
(
−
1
/
2
)
(
x
2
)
{\displaystyle H_{2n}(x)=(-1)^{n}\ 2^{2n}\ n!\ L_{n}^{(-1/2)}(x^{2})}
以及
H
2
n
+
1
(
x
)
=
(
−
1
)
n
2
2
n
+
1
n
!
x
L
n
(
1
/
2
)
(
x
2
)
{\displaystyle H_{2n+1}(x)=(-1)^{n}\ 2^{2n+1}\ n!\ x\ L_{n}^{(1/2)}(x^{2})}
这里的H n x 2 )的埃爾米特多項式 (所谓的“物理学家形式”)。
正因为这样,广义拉盖尔多项式也在量子谐振子 的量子力学处理中出现。
与超几何函数的关系 [ 编辑 ] 拉盖尔多项式可以用超几何函数 来定义,具体地说,是用合流超几何函数 定义:
L
n
(
α
)
(
x
)
=
(
n
+
α
n
)
M
(
−
n
,
α
+
1
,
x
)
=
(
α
+
1
)
n
n
!
1
F
1
(
−
n
,
α
+
1
,
x
)
{\displaystyle L_{n}^{(\alpha )}(x)={n+\alpha \choose n}M(-n,\alpha +1,x)={\frac {(\alpha +1)_{n}}{n!}}\,_{1}F_{1}(-n,\alpha +1,x)}
(
a
)
n
{\displaystyle (a)_{n}}
阶乘幂 ,这里表示升阶乘 。
与贝塞尔函数的关系 [ 编辑 ] 拉盖尔多项式与变形贝塞尔函数 之间有以下关系:
L
n
(
α
)
(
x
)
=
e
x
2
(
x
4
)
n
+
1
2
2
π
(
n
+
1
)
!
(
−
1
2
n
+
1
)
⋅
⋅
∑
k
=
0
n
(
−
1
)
k
+
1
(
2
n
+
1
n
−
k
)
(
n
+
α
n
)
(
α
+
2
n
+
1
n
−
k
)
(
n
−
k
+
α
n
−
k
)
(
k
+
1
2
)
K
k
+
1
2
(
x
2
)
=
e
x
2
(
4
x
)
n
+
α
+
1
2
Γ
(
α
+
1
2
)
(
−
α
−
1
n
)
(
−
α
−
1
2
n
)
⋅
⋅
n
!
∑
k
=
0
n
(
−
2
n
−
1
−
2
α
k
−
n
)
(
−
2
n
−
1
−
α
k
−
n
)
(
−
α
−
1
k
−
n
)
(
α
+
1
2
+
k
)
I
α
+
1
2
+
k
(
x
2
)
,
{\displaystyle {\begin{aligned}L_{n}^{(\alpha )}(x)=&e^{\frac {x}{2}}\left({\frac {x}{4}}\right)^{n+{\frac {1}{2}}}{\frac {2}{{\sqrt {\pi }}(n+1)!{-{\frac {1}{2}} \choose n+1}}}\cdot \\&\cdot \sum _{k=0}^{n}(-1)^{k+1}{2n+1 \choose n-k}{\frac {{n+\alpha \choose n}{\alpha +2n+1 \choose n-k}}{n-k+\alpha \choose n-k}}\left(k+{\frac {1}{2}}\right)K_{k+{\frac {1}{2}}}\left({\frac {x}{2}}\right)\\=&e^{\frac {x}{2}}\left({\frac {4}{x}}\right)^{n+\alpha +{\frac {1}{2}}}\Gamma \left(\alpha +{\frac {1}{2}}\right){-\alpha -1 \choose n}{-\alpha -{\frac {1}{2}} \choose n}\cdot \\&\cdot n!\sum _{k=0}^{n}{\frac {{-2n-1-2\alpha \choose k-n}{-2n-1-\alpha \choose k-n}}{-\alpha -1 \choose k-n}}\left(\alpha +{\frac {1}{2}}+k\right)I_{\alpha +{\frac {1}{2}}+k}\left({\frac {x}{2}}\right)\end{aligned}},}
进一步有:
L
n
(
α
)
(
x
)
=
2
4
n
(
2
n
+
1
)
(
−
1
2
n
)
∑
k
=
0
n
(
k
+
1
2
)
(
2
n
+
1
n
−
k
)
(
n
k
)
2
(
n
+
α
k
)
(
2
n
+
α
+
1
n
−
k
)
x
n
−
k
(
n
−
k
)
!
L
k
−
2
k
−
1
(
x
)
.
{\displaystyle L_{n}^{(\alpha )}(x)={\frac {2}{4^{n}(2n+1){-{\frac {1}{2}} \choose n}}}\sum _{k=0}^{n}\left(k+{\frac {1}{2}}\right){\frac {2n+1 \choose n-k}{{n \choose k}^{2}}}{n+\alpha \choose k}{2n+\alpha +1 \choose n-k}{\frac {x^{n-k}}{(n-k)!}}L_{k}^{-2k-1}(x).}
外部链接 [ 编辑 ]
^ Abramowitz, p. 506, 13.3.8 (页面存档备份 ,存于互联网档案馆 )
参考文献 [ 编辑 ] Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 22 (页面存档备份 ,存于互联网档案馆 )", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, ISBN 0-486-61272-4 .
B Spain, M G Smith, Functions of mathematical physics , Van Nostrand Reinhold Company, London, 1970. Chapter 10 deals with Laguerre polynomials.
Eric W. Weisstein, "Laguerre Polynomial (页面存档备份 ,存于互联网档案馆 )", From MathWorld—A Wolfram Web Resource.
George Arfken and Hans Weber. Mathematical Methods for Physicists. Academic Press. 2000. ISBN 0-12-059825-6 S. S. Bayin (2006), Mathematical Methods in Science and Engineering , Wiley, Chapter 3. 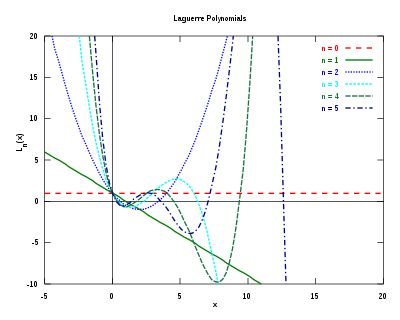

















![{\displaystyle E\left[L_{n}(X)L_{m}(X)\right]=0\ {\mbox{whenever}}\ n\neq m.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dfce23a3e74e527e067dcbe0fb05ad0cf768a63)











![{\displaystyle (0,n+\alpha +(n-1){\sqrt {n+\alpha }}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2f94def16cdcc2ced729d4e45d7152000ed5453)





































![{\displaystyle \int _{0}^{\infty }x^{\alpha +1}e^{-x}\left[L_{n}^{(\alpha )}\right]^{2}dx={\frac {(n+\alpha )!}{n!}}(2n+\alpha +1).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb41ec3fea5cdbbd653107cdb8067455a1cbccb9)


































