图1 贝塞尔函数的一个实例:一个紧绷的鼓面在中心受到敲击后的二阶振动振型,其振幅沿半径方向上的分布就是一个贝塞尔函数(考虑正负号)。实际生活中受敲击的鼓面的振动是各阶类似振动形态的叠加。贝塞尔函数 (Bessel functions ),是数学上的一类特殊函数 的总称。通常单说的贝塞尔函数 指第一类贝塞尔函数 Bessel function of the first kind )。一般贝塞尔函数是下列常微分方程 (一般称为贝塞尔方程 )的标准解函数
y
(
x
)
{\displaystyle y(x)}
x
2
d
2
y
d
x
2
+
x
d
y
d
x
+
(
x
2
−
α
2
)
y
=
0
{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}+(x^{2}-\alpha ^{2})y=0}
该方程的通解无法用初等函数 表示。
由於贝塞尔微分方程是二階常微分方程 ,需要由兩個獨立的函數來表示其标准解函数。典型的是使用第一类贝塞尔函数 和第二类贝塞尔函数 來表示标准解函数:
y
(
x
)
=
c
1
J
α
(
x
)
+
c
2
Y
α
(
x
)
{\displaystyle y(x)=c_{1}J_{\alpha }(x)+c_{2}Y_{\alpha }(x)}
注意,由於
Y
α
(
x
)
{\displaystyle Y_{\alpha }(x)}
發散 的(無窮 ),當取 x=0 時,相關係數
c
2
{\displaystyle c_{2}}
贝塞尔函数的具体形式随上述方程中任意实数或複數α变化而变化(相应地,α被称为其对应贝塞尔函数的阶数 整数 n ,对应解称为n 阶贝塞尔函数
尽管在上述微分方程中,α本身的正负号不改变方程的形式,但实际应用中仍习惯针对α和−α定义两种不同的贝塞尔函数(这样做能带来好处,比如消除了函数在α=0 点的不光滑性)。
贝塞尔函數也被稱為柱諧函數 圓柱函數 或圓柱諧波 ,因為他們是於拉普拉斯方程 在圓柱坐標 上的求解過程中被發現的。
贝塞尔函数的几个正整数阶特例早在18世纪中叶就由瑞士 数学家 丹尼尔·伯努利 在研究悬链振动时提出了,当时引起了数学界的兴趣。丹尼尔 的叔叔雅各布·伯努利 ,欧拉 、拉格朗日 等数学大师对贝塞尔函数的研究作出过重要贡献。1817年,德国 数学家贝塞尔 在研究开普勒 提出的三体引力 系统的运动问题时,第一次系统地提出了贝塞尔函数的总体理论框架,后人以他的名字来命名了这种函数 [1] [2] (页面存档备份 ,存于互联网档案馆 )。
现实背景和应用范围 [ 编辑 ] 贝塞尔方程是在圆柱坐标 或球坐标 下使用分离变量法 求解拉普拉斯方程 和亥姆霍兹方程 时得到的(在圆柱域问题中得到的是整阶 形式 α = n ;在球形域问题中得到的是半奇数阶 形式 α = n +½),因此贝塞尔函数在波的传播 问题以及各种涉及有势场 的问题中占有非常重要的地位,最典型的问题有:
在其他一些领域,贝塞尔函数也相当有用。譬如在ttf字体文件压缩,信号处理 中的调频合成 凯泽窗 的定义中,都要用到贝塞尔函数。
贝塞尔方程是一个二阶常微分方程,必然存在两个线性无关 的解。针对各种具体情况,人们提出了表示这些解的不同形式。下面分别介绍这些不同类型的贝塞尔函数。
第一类贝塞尔函数 [ 编辑 ] 图2 0阶、1阶和2阶第一类贝塞尔函数(贝塞尔J函数)曲线第一类贝塞尔函数 (Bessel function of the first kind ),又称贝塞尔函数 (Bessel function ),下文中有时会简称为J函数 ,記作J α
第一类α阶贝塞尔函数J α (x )是贝塞尔方程当α为整数或α非负时的解,须满足在x = 0 时有限。这样选取和处理J α 的原因见本主题下面的性质介绍 ;另一种定义方法是通过它在x = 0 点的泰勒级数 展开(或者更一般地通过幂级数 展开,这适用于α为非整数):
J
α
(
x
)
=
∑
m
=
0
∞
(
−
1
)
m
m
!
Γ
(
m
+
α
+
1
)
(
x
2
)
2
m
+
α
{\displaystyle J_{\alpha }(x)=\sum _{m=0}^{\infty }{\frac {(-1)^{m}}{m!\Gamma (m+\alpha +1)}}{\left({\frac {x}{2}}\right)}^{2m+\alpha }}
上式中
Γ
(
z
)
{\displaystyle \Gamma (z)}
Γ函数 (它可视为阶乘 函数向非整型自变量 的推广)。第一类贝塞尔函数的形状大致与按
1
/
x
{\displaystyle 1/{\sqrt {x}}}
正弦 或余弦 函数类似(参见本页下面对它们渐近形式的介绍),但它们的零点并不是周期性的,另外随着x 的增加,零点的间隔会越来越接近周期性。图2所示为0阶、1阶和2阶第一类贝塞尔函数
J
α
(
x
)
{\displaystyle J_{\alpha }(x)}
α
=
0
,
1
,
2
{\displaystyle \alpha =0,1,2}
如果α不为整数,则
J
α
(
x
)
{\displaystyle J_{\alpha }(x)}
J
−
α
(
x
)
{\displaystyle J_{-\alpha }(x)}
解系 。反之若
α
{\displaystyle \alpha }
J
−
α
(
x
)
=
(
−
1
)
α
J
α
(
x
)
{\displaystyle J_{-\alpha }(x)=(-1)^{\alpha }J_{\alpha }(x)\,}
于是两函数之间已不满足线性无关条件。为寻找在此情况下微分方程与
J
α
(
x
)
{\displaystyle J_{\alpha }(x)}
第二类贝塞尔函数 ,定义过程将在后面的小节中给出。
贝塞尔积分 [ 编辑 ]
α
{\displaystyle \alpha }
J
α
(
x
)
=
1
2
π
∫
0
2
π
cos
(
α
τ
−
x
sin
τ
)
d
τ
.
{\displaystyle J_{\alpha }(x)={\frac {1}{2\pi }}\int _{0}^{2\pi }\cos(\alpha \tau -x\sin \tau )d\tau .}
(
α
{\displaystyle \alpha }
参考文献[2] 第360页)
这个积分式就是贝塞尔当年提出的定义,而且他还从该定义中推出了函数的一些性质。另一种积分表达式为:
J
α
(
x
)
=
1
2
π
∫
−
π
π
e
i
(
α
τ
−
x
sin
τ
)
d
τ
{\displaystyle J_{\alpha }(x)={\frac {1}{2\pi }}\int _{-\pi }^{\pi }e^{i(\alpha \tau -x\sin \tau )}d\tau }
和超几何级数的关系 [ 编辑 ] 贝塞尔函数可以用超几何级数 表示成下面的形式:
J
α
(
z
)
=
(
z
/
2
)
α
Γ
(
α
+
1
)
0
F
1
(
α
+
1
;
−
z
2
/
4
)
.
{\displaystyle J_{\alpha }(z)={\frac {(z/2)^{\alpha }}{\Gamma (\alpha +1)}}\;_{0}F_{1}(\alpha +1;-z^{2}/4).}
ɑ為整數。由於函數線性相關的特性(用了一個就少了一個,所以要再構造一個),才需定義如下詳細介紹的第二類貝塞爾函數。
第二类贝塞尔函数(诺依曼函数) [ 编辑 ] 图3 0阶、1阶和2阶第二类贝塞尔函数(贝塞尔Y 函数)曲线图第二类贝塞尔函数 (Bessel function of the second kind ),又称诺伊曼函数 (Neumann function ),下文中有时会简称为Y函数 ,記作Y α
第二类贝塞尔函数也许比第一类更为常用。
这种函数通常用Y α (x )表示,它们是贝塞尔方程的另一类解。x = 0 点是第二类贝塞尔函数的(无穷)奇点。
Y α (x )又被称为诺依曼函数 (Neumann function),有时也记作N α (x )。它和J α (x )存在如下关系:
Y
α
(
x
)
=
J
α
(
x
)
cos
(
α
π
)
−
J
−
α
(
x
)
sin
(
α
π
)
,
{\displaystyle Y_{\alpha }(x)={\frac {J_{\alpha }(x)\cos(\alpha \pi )-J_{-\alpha }(x)}{\sin(\alpha \pi )}},}
若α为整数(此时上式是
0
0
{\displaystyle {\frac {0}{0}}}
未定式 )则取右端的极限 值。
从前面对J α (x )的定义可以知道,若α不为整数时,定义Y α 是多余的(因为贝塞尔方程的两个线性无关解都已经用J函数表示出来了)。另一方面,若α为整数,Y α J α
Y
−
n
(
x
)
=
(
−
1
)
n
Y
n
(
x
)
{\displaystyle Y_{-n}(x)=(-1)^{n}Y_{n}(x)\,}
J α (x )和Y α (x )均为沿负实半轴割开的复平面 内关于x 的全纯函数 。当α为整数时,复平面内不存在贝塞尔函数的支点 ,所以J 和Y 均为x 的整函数 。若将x 固定,则贝塞尔函数是α的整函数。图3所示为0阶、1阶和2阶第二类贝塞尔函数
Y
α
(
x
)
{\displaystyle Y_{\alpha }(x)}
α
=
0
,
1
,
2
{\displaystyle \alpha =0,1,2}
第三类贝塞尔函数(汉克尔函数) [ 编辑 ] 第三类贝塞尔函数 (Bessel function of the third kind ),又称汉克尔函数 (Hankel function )。
贝塞尔方程的另外一对重要的线性无关解称为汉克尔 函数H α (1) (x )和H α (2) (x ),分别定义为:
H
α
(
1
)
(
x
)
=
J
α
(
x
)
+
i
Y
α
(
x
)
{\displaystyle H_{\alpha }^{(1)}(x)=J_{\alpha }(x)+iY_{\alpha }(x)}
H
α
(
2
)
(
x
)
=
J
α
(
x
)
−
i
Y
α
(
x
)
{\displaystyle H_{\alpha }^{(2)}(x)=J_{\alpha }(x)-iY_{\alpha }(x)}
其中i 为虚数 单位
−
1
{\displaystyle {\sqrt {-1}}}
第三类贝塞尔函数 ;它们描述了二维波动方程 的外向行柱面波 解和内向行柱面波 解("行"与在"行动"中同音)。
利用前面推出的关系可将汉克尔函数表示成:
H
α
(
1
)
(
x
)
=
J
−
α
(
x
)
−
e
−
α
π
i
J
α
(
x
)
i
sin
(
α
π
)
{\displaystyle H_{\alpha }^{(1)}(x)={\frac {J_{-\alpha }(x)-e^{-\alpha \pi i}J_{\alpha }(x)}{i\sin(\alpha \pi )}}}
H
α
(
2
)
(
x
)
=
J
−
α
(
x
)
−
e
α
π
i
J
α
(
x
)
−
i
sin
(
α
π
)
{\displaystyle H_{\alpha }^{(2)}(x)={\frac {J_{-\alpha }(x)-e^{\alpha \pi i}J_{\alpha }(x)}{-i\sin(\alpha \pi )}}}
若α为整数,则须对等号右边取极限值。另外,无论α是不是整数,下面的关系都成立:
H
−
α
(
1
)
(
x
)
=
e
α
π
i
H
α
(
1
)
(
x
)
{\displaystyle H_{-\alpha }^{(1)}(x)=e^{\alpha \pi i}H_{\alpha }^{(1)}(x)}
H
−
α
(
2
)
(
x
)
=
e
−
α
π
i
H
α
(
2
)
(
x
)
{\displaystyle H_{-\alpha }^{(2)}(x)=e^{-\alpha \pi i}H_{\alpha }^{(2)}(x)}
修正贝塞尔函数 [ 编辑 ] 贝塞尔函数当变量x 为复数 时同样成立,并且当x 为纯虚数 时能得到一类重要情形——它们被称为第一类修正贝塞尔函数 (modified Bessel function of the first kind )和第二类修正贝塞尔函数 (modified Bessel function of the second kind ),或虚变量的贝塞尔函数 (有时还称为双曲型贝塞尔函数 ),定义为:
I
α
(
x
)
=
i
−
α
J
α
(
i
x
)
{\displaystyle I_{\alpha }(x)=i^{-\alpha }J_{\alpha }(ix)\!}
K
α
(
x
)
=
π
2
I
−
α
(
x
)
−
I
α
(
x
)
sin
(
α
π
)
=
π
2
i
α
+
1
H
α
(
1
)
(
i
x
)
{\displaystyle K_{\alpha }(x)={\frac {\pi }{2}}{\frac {I_{-\alpha }(x)-I_{\alpha }(x)}{\sin(\alpha \pi )}}={\frac {\pi }{2}}i^{\alpha +1}H_{\alpha }^{(1)}(ix)\!}
以上形式保证了当变量x 为实数 时,函数值亦为实数。这两个函数构成了下列修正贝塞尔方程 (与一般贝塞尔方程的差别仅在两个正负号)的一个相互线性无关的解系:
x
2
d
2
y
d
x
2
+
x
d
y
d
x
−
(
x
2
+
α
2
)
y
=
0.
{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}-(x^{2}+\alpha ^{2})y=0.}
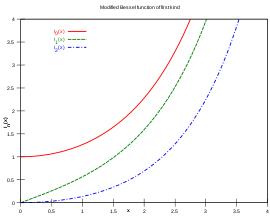
修正贝塞尔函数与一般贝塞尔函数的差别在于:一般贝塞尔函数随实变量是振荡型的,而修正贝塞尔函数I α 和K α 则分别是指数增长 和指数衰减 型的。和第一类贝塞尔函数J α 一样,函数I α 当α > 0 时在x =0 点等于0,当α=0时在x =0 点趋于有限值。类似地,K α 在x =0 点发散(趋于无穷)。
图4-1 第一类修正贝塞尔函数
I
α
(
x
)
{\displaystyle I_{\alpha }(x)}
α
=
0
,
1
,
2
{\displaystyle \alpha =0,1,2}
图4-2 第二类修正贝塞尔函数
K
α
(
x
)
{\displaystyle K_{\alpha }(x)}
α
=
0
,
1
,
2
{\displaystyle \alpha =0,1,2}
复数变量的贝塞尔函数之零值 :
J
α
(
x
)
=
0
{\displaystyle J_{\alpha }(x)=0}
参考文献[5] )。
第二类修正贝塞尔函数有时候被称为第三类修正贝塞尔函数 (modified Bessel function of the third kind )。
球贝塞尔函数 [ 编辑 ] 图5-1 第一类球贝塞尔函数
j
n
(
x
)
{\displaystyle j_{n}(x)}
n
=
0
,
1
,
2
{\displaystyle n=0,1,2}
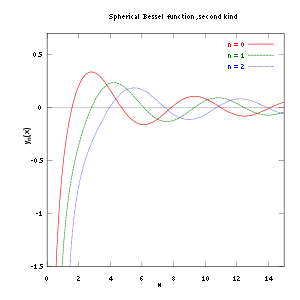
图5-2 第二类球贝塞尔函数
y
n
(
x
)
{\displaystyle y_{n}(x)}
n
=
0
,
1
,
2
{\displaystyle n=0,1,2}
若使用分离变量法 求解球坐标 下的三维亥姆霍兹方程 ,则可得到如下形式关于径向(r 方向)分量的常微分方程 :
x
2
d
2
y
d
x
2
+
2
x
d
y
d
x
+
[
x
2
−
n
(
n
+
1
)
]
y
=
0.
{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+2x{\frac {dy}{dx}}+[x^{2}-n(n+1)]y=0.}
关于上述方程的一对线性无关解称为球贝塞尔函数 ,分别用j n y n n n J n Y n
j
n
(
x
)
=
π
2
x
J
n
+
1
/
2
(
x
)
,
{\displaystyle j_{n}(x)={\sqrt {\frac {\pi }{2x}}}J_{n+1/2}(x),}
y
n
(
x
)
=
π
2
x
Y
n
+
1
/
2
(
x
)
=
(
−
1
)
n
+
1
π
2
x
J
−
n
−
1
/
2
(
x
)
.
{\displaystyle y_{n}(x)={\sqrt {\frac {\pi }{2x}}}Y_{n+1/2}(x)=(-1)^{n+1}{\sqrt {\frac {\pi }{2x}}}J_{-n-1/2}(x).}
球贝塞尔函数也可写成:
j
n
(
x
)
=
(
−
x
)
n
(
1
x
d
d
x
)
n
sin
x
x
,
{\displaystyle j_{n}(x)=(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}\,{\frac {\sin x}{x}},}
y
n
(
x
)
=
−
(
−
x
)
n
(
1
x
d
d
x
)
n
cos
x
x
.
{\displaystyle y_{n}(x)=-(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}\,{\frac {\cos x}{x}}.}
0阶第一类球贝塞尔函数
j
0
(
x
)
{\displaystyle j_{0}(x)}
sinc函数 。头几阶整阶球贝塞尔函数的表达式分别为:
第一类:
j
0
(
x
)
=
sin
x
x
{\displaystyle j_{0}(x)={\frac {\sin x}{x}}}
j
1
(
x
)
=
sin
x
x
2
−
cos
x
x
{\displaystyle j_{1}(x)={\frac {\sin x}{x^{2}}}-{\frac {\cos x}{x}}}
j
2
(
x
)
=
(
3
x
2
−
1
)
sin
x
x
−
3
cos
x
x
2
{\displaystyle j_{2}(x)=\left({\frac {3}{x^{2}}}-1\right){\frac {\sin x}{x}}-{\frac {3\cos x}{x^{2}}}}
第二类:
y
0
(
x
)
=
−
j
−
1
(
x
)
=
−
cos
x
x
{\displaystyle y_{0}(x)=-j_{-1}(x)=-\,{\frac {\cos x}{x}}}
y
1
(
x
)
=
j
−
2
(
x
)
=
−
cos
x
x
2
−
sin
x
x
{\displaystyle y_{1}(x)=j_{-2}(x)=-\,{\frac {\cos x}{x^{2}}}-{\frac {\sin x}{x}}}
y
2
(
x
)
=
−
j
−
3
(
x
)
=
(
−
3
x
2
+
1
)
cos
x
x
−
3
sin
x
x
2
.
{\displaystyle y_{2}(x)=-j_{-3}(x)=\left(-\,{\frac {3}{x^{2}}}+1\right){\frac {\cos x}{x}}-{\frac {3\sin x}{x^{2}}}.}
还可以依照前面构造汉克尔函数相同的步骤构造所谓球汉克尔函数 :
h
n
(
1
)
(
x
)
=
j
n
(
x
)
+
i
y
n
(
x
)
{\displaystyle h_{n}^{(1)}(x)=j_{n}(x)+iy_{n}(x)}
h
n
(
2
)
(
x
)
=
j
n
(
x
)
−
i
y
n
(
x
)
.
{\displaystyle h_{n}^{(2)}(x)=j_{n}(x)-iy_{n}(x).}
事实上,所有半奇数阶贝塞尔函数都可以写成由三角函数 组成的封闭形式的表达式,球贝塞尔函数也同样可以。特别地,对所有非负整数n ,存在:
h
n
(
1
)
(
x
)
=
(
−
i
)
n
+
1
e
i
x
x
∑
m
=
0
n
i
m
m
!
(
2
x
)
m
(
n
+
m
)
!
!
(
n
−
m
)
!
!
{\displaystyle h_{n}^{(1)}(x)=(-i)^{n+1}{\frac {e^{ix}}{x}}\sum _{m=0}^{n}{\frac {i^{m}}{m!(2x)^{m}}}{\frac {(n+m)!!}{(n-m)!!}}}
而对实自变量x ,h n (2) 是上面h n (1) 的复共轭(!! 表示双阶乘 )。由此我们可以通过得到h ,再分离实部虚部,求出相应阶j 和h 的表达式,譬如j 0 (x ) = sin(x )/x ,y 0 (x ) = -cos(x )/x ,等等。
球贝塞尔函数的生成函数为:
1
z
cos
(
z
2
−
2
z
t
)
=
∑
n
=
0
∞
t
n
n
!
j
n
−
1
(
z
)
,
{\displaystyle {\frac {1}{z}}\cos({\sqrt {z^{2}-2zt}})=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}j_{n-1}(z),}
1
z
sin
(
z
2
−
2
z
t
)
=
∑
n
=
0
∞
t
n
n
!
y
n
−
1
(
z
)
.
{\displaystyle {\frac {1}{z}}\sin({\sqrt {z^{2}-2zt}})=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}y_{n-1}(z).}
Sn Cn ξn ζn [ 编辑 ] 黎卡提-贝塞尔函数(Riccati-Bessel functions)和球贝塞尔函数比较类似:
S
n
(
x
)
=
x
j
n
(
x
)
=
π
x
/
2
J
n
+
1
/
2
(
x
)
{\displaystyle S_{n}(x)=xj_{n}(x)={\sqrt {\pi x/2}}J_{n+1/2}(x)}
C
n
(
x
)
=
−
x
y
n
(
x
)
=
−
π
x
/
2
Y
n
+
1
/
2
(
x
)
{\displaystyle C_{n}(x)=-xy_{n}(x)=-{\sqrt {\pi x/2}}Y_{n+1/2}(x)}
ζ
n
(
x
)
=
x
h
n
(
2
)
(
x
)
=
π
x
/
2
H
n
+
1
/
2
(
2
)
(
x
)
=
S
n
(
x
)
+
i
C
n
(
x
)
{\displaystyle \zeta _{n}(x)=xh_{n}^{(2)}(x)={\sqrt {\pi x/2}}H_{n+1/2}^{(2)}(x)=S_{n}(x)+iC_{n}(x)}
该函数满足方程:
x
2
d
2
y
d
x
2
+
[
x
2
−
n
(
n
+
1
)
]
y
=
0
{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+[x^{2}-n(n+1)]y=0}
这个方程以及相应的黎卡提-贝塞尔解 是德国 物理学家 古斯塔夫·米 (Gustav Mie )于1908年研究电磁波 在球状颗粒表面散射 问题时提出的,后人将这种散射称为米氏散射 (Mie scattering )。这个问题近几年的进展可参见文献 Du (2004)。
后人有时会遵从德拜 (Debye )在1909年的论文中的记法,用
ψ
n
,
χ
n
{\displaystyle \psi _{n},\chi _{n}}
S
n
,
C
n
{\displaystyle S_{n},C_{n}}
渐近形式 [ 编辑 ] 贝塞尔函数在α非负时具有下面的渐近形式。当自变量x 为小量,即
0
<
x
≪
α
+
1
{\displaystyle 0<x\ll {\sqrt {\alpha +1}}}
J
α
(
x
)
→
1
Γ
(
α
+
1
)
(
x
2
)
α
{\displaystyle J_{\alpha }(x)\rightarrow {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {x}{2}}\right)^{\alpha }}
Y
α
(
x
)
→
{
2
π
[
ln
(
x
/
2
)
+
γ
]
if
α
=
0
−
Γ
(
α
)
π
(
2
x
)
α
if
α
>
0
{\displaystyle Y_{\alpha }(x)\rightarrow \left\{{\begin{matrix}{\frac {2}{\pi }}\left[\ln(x/2)+\gamma \right]&{\mbox{if }}\alpha =0\\\\-{\frac {\Gamma (\alpha )}{\pi }}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{if }}\alpha >0\end{matrix}}\right.}
式中γ为歐拉-馬歇羅尼常數 (也叫歐拉常數,等于 0.5772156649...),Γ为Γ函数 。对于很大的x ,即
x
≫
|
α
2
−
1
/
4
|
{\displaystyle x\gg |\alpha ^{2}-1/4|}
J
α
(
x
)
→
2
π
x
cos
(
x
−
α
π
2
−
π
4
)
{\displaystyle J_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\cos \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right)}
Y
α
(
x
)
→
2
π
x
sin
(
x
−
α
π
2
−
π
4
)
.
{\displaystyle Y_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\sin \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right).}
(α=1/2 时渐近号两边严格相等;参见前面对球贝塞尔函数的介绍)。其他形式贝塞尔函数的渐近形式可以从上面的式子直接推得。譬如,对大自变量
x
≫
|
α
2
−
1
/
4
|
{\displaystyle x\gg |\alpha ^{2}-1/4|}
I
α
(
x
)
→
1
2
π
x
e
x
,
{\displaystyle I_{\alpha }(x)\rightarrow {\frac {1}{\sqrt {2\pi x}}}e^{x},}
K
α
(
x
)
→
π
2
x
e
−
x
.
{\displaystyle K_{\alpha }(x)\rightarrow {\sqrt {\frac {\pi }{2x}}}e^{-x}.}
对小自变量
0
<
x
≪
α
+
1
{\displaystyle 0<x\ll {\sqrt {\alpha +1}}}
I
α
(
x
)
→
1
Γ
(
α
+
1
)
(
x
2
)
α
{\displaystyle I_{\alpha }(x)\rightarrow {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {x}{2}}\right)^{\alpha }}
K
α
(
x
)
→
{
−
ln
(
x
/
2
)
−
γ
if
α
=
0
Γ
(
α
)
2
(
2
x
)
α
if
α
>
0
{\displaystyle K_{\alpha }(x)\rightarrow \left\{{\begin{matrix}-\ln(x/2)-\gamma &{\mbox{if }}\alpha =0\\\\{\frac {\Gamma (\alpha )}{2}}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{if }}\alpha >0\end{matrix}}\right.}
整阶(α = n )第一类贝塞尔函数J n 母函数 generating function )的罗朗级数 (Laurent series )展开来定义:
e
(
x
/
2
)
(
t
−
1
/
t
)
=
∑
n
=
−
∞
∞
J
n
(
x
)
t
n
,
{\displaystyle e^{(x/2)(t-1/t)}=\sum _{n=-\infty }^{\infty }J_{n}(x)t^{n},}
上式得左边即为整阶第一类贝塞尔函数的母函数,这是丹麦 天文学家 汉森 于1843年提出的。(这种定义也可以通过路径积分 或其他方法推广到非整数阶)。整阶函数的另一个重要性质是下列雅可比-安格尔恒等式 (Jacobi-Anger identity ):
e
i
z
cos
ϕ
=
∑
n
=
−
∞
∞
i
n
J
n
(
z
)
e
i
n
ϕ
,
{\displaystyle e^{iz\cos \phi }=\sum _{n=-\infty }^{\infty }i^{n}J_{n}(z)e^{in\phi },}
利用这一等式可以将平面波 展开成一系列柱面波的叠加,或者将调频 信号分解成傅里叶级数 的叠加。
函数J α 、Y α 、H α (1) 和H α (2) 均满足递推关系 :
Z
α
−
1
(
x
)
+
Z
α
+
1
(
x
)
=
2
α
x
Z
α
(
x
)
{\displaystyle Z_{\alpha -1}(x)+Z_{\alpha +1}(x)={\frac {2\alpha }{x}}Z_{\alpha }(x)}
Z
α
−
1
(
x
)
−
Z
α
+
1
(
x
)
=
2
d
Z
α
d
x
{\displaystyle Z_{\alpha -1}(x)-Z_{\alpha +1}(x)=2{\frac {dZ_{\alpha }}{dx}}}
其中Z 代表J , Y , H (1) 或H (2) 。(常将这两个恒等式联立推出其他关系)。从这组递推关系可以通过低阶贝塞尔函数(或它们的低阶导数 )计算高阶贝塞尔函数(或它们的高阶导数 )。特别地,有:
(
d
x
d
x
)
m
[
x
α
Z
α
(
x
)
]
=
x
α
−
m
Z
α
−
m
(
x
)
{\displaystyle \left({\frac {d}{xdx}}\right)^{m}\left[x^{\alpha }Z_{\alpha }(x)\right]=x^{\alpha -m}Z_{\alpha -m}(x)}
(
d
x
d
x
)
m
[
Z
α
(
x
)
x
α
]
=
(
−
1
)
m
Z
α
+
m
(
x
)
x
α
+
m
{\displaystyle \left({\frac {d}{xdx}}\right)^{m}\left[{\frac {Z_{\alpha }(x)}{x^{\alpha }}}\right]=(-1)^{m}{\frac {Z_{\alpha +m}(x)}{x^{\alpha +m}}}}
由于贝塞尔方程对应的作用算符除以x 后便是一个(自伴随 的)厄米算符 (Hermitian ),所以它的解在适当的边界条件 下须满足正交性关系。特别地,可推得:
∫
0
1
x
J
α
(
x
u
α
,
m
)
J
α
(
x
u
α
,
n
)
d
x
=
δ
m
,
n
2
J
α
+
1
(
u
α
,
m
)
2
,
{\displaystyle \int _{0}^{1}xJ_{\alpha }(xu_{\alpha ,m})J_{\alpha }(xu_{\alpha ,n})dx={\frac {\delta _{m,n}}{2}}J_{\alpha +1}(u_{\alpha ,m})^{2},}
其中α > -1,δm ,n 克罗内克δ ,u α,m 表示J α (x )的第m 级零点 。这个正交性关系可用于计算傅里叶-贝塞尔级数 中各项的系数,以利用该级数将任意函数写成α固定、m 变化的函数J α (x u α,m )的无穷叠加形式。(可以立即得到球贝塞尔函数相应的关系)。
另一个正交性关系是下列在α > -1/2时成立的“封闭方程”(closure equation ):
∫
0
∞
x
J
α
(
u
x
)
J
α
(
v
x
)
d
x
=
1
u
δ
(
u
−
v
)
{\displaystyle \int _{0}^{\infty }xJ_{\alpha }(ux)J_{\alpha }(vx)dx={\frac {1}{u}}\delta (u-v)}
其中δ为狄拉克δ函数 。球贝塞尔函数的正交性条件为(当α > 0):
∫
0
∞
x
2
j
α
(
u
x
)
j
α
(
v
x
)
d
x
=
π
2
u
2
δ
(
u
−
v
)
{\displaystyle \int _{0}^{\infty }x^{2}j_{\alpha }(ux)j_{\alpha }(vx)dx={\frac {\pi }{2u^{2}}}\delta (u-v)}
贝塞尔方程的另一个重要性质与其朗斯基行列式 (Wronskian )相关,由阿贝尔恒等式 (Abel's identity )得到:
A
α
(
x
)
d
B
α
d
x
−
d
A
α
d
x
B
α
(
x
)
=
C
α
x
,
{\displaystyle A_{\alpha }(x){\frac {dB_{\alpha }}{dx}}-{\frac {dA_{\alpha }}{dx}}B_{\alpha }(x)={\frac {C_{\alpha }}{x}},}
其中A α 和B α 是贝塞尔方程的任意两个解,C α 是与x 无关的常数(由α和贝塞尔函数的种类决定)。譬如,若A α = J α 、B α = Y α ,则C α is 2/π。该性质在修正贝塞尔函数中同样适用,譬如,若A α = I α 、B α = K α ,则C α 为-1。
参考文献 [ 编辑 ] [1] 严镇军编,《数学物理方程》,第二版,中国科学技术大学出版社,合肥,2002,第82页~第123页,ISBN 7-312-00799-6
[2] Milton Abramowitz and Irene A. Stegun, eds., Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (Dover: New York, 1972) (英文)
[3] George B. Arfken and Hans J. Weber, Mathematical Methods for Physicists (Harcourt: San Diego, 2001).
[4] Frank Bowman, Introduction to Bessel Functions (Dover: New York, 1958) ISBN 0-486-60462-4 .
[5] G. N. Watson, A Treatise on the Theory of Bessel Functions, Second Edition , (1966) Cambridge University Press.
[6] G. Mie, "Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen", Ann. Phys. Leipzig 25 (1908), p.377.
[7] Hong Du, "Mie-scattering calculation," Applied Optics 43 (9), 1951-1956 (2004). 外部链接 [ 编辑 ] 








































![{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+2x{\frac {dy}{dx}}+[x^{2}-n(n+1)]y=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfd13e94863668203e3a8e5078ce0a6071c95b2b)



















![{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+[x^{2}-n(n+1)]y=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7795a623edf57ced1f95d670ca137aa5521660b5)




![{\displaystyle Y_{\alpha }(x)\rightarrow \left\{{\begin{matrix}{\frac {2}{\pi }}\left[\ln(x/2)+\gamma \right]&{\mbox{if }}\alpha =0\\\\-{\frac {\Gamma (\alpha )}{\pi }}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{if }}\alpha >0\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c5777c6e6b7d6bc4064ded1cfb6dc31924c18c8)











![{\displaystyle \left({\frac {d}{xdx}}\right)^{m}\left[x^{\alpha }Z_{\alpha }(x)\right]=x^{\alpha -m}Z_{\alpha -m}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a5672cc4e621bb81e213314895df6ee45c8306b)
![{\displaystyle \left({\frac {d}{xdx}}\right)^{m}\left[{\frac {Z_{\alpha }(x)}{x^{\alpha }}}\right]=(-1)^{m}{\frac {Z_{\alpha +m}(x)}{x^{\alpha +m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c893320b4de90b0ae6f4341b45f589400aa5cd5)



