极限 (范畴论)

  关于与「极限 (范畴论)」標題相近或相同的条目页，請見「极限」。

在數學裡的範疇論中，極限（英語：Limit）的概念融貫了多種構造，包括和、積等等；範疇論中許多泛性質也可從極限來理解。

極限分為極限與餘極限（又稱上極限），彼此的定義相對偶。在不同場合的別名及英譯如下表：

餘極限/上極限（colimit）	正（向）極限（direct limit）	歸納極限（inductive limit）
極限（limit）	逆（向）極限（inverse limit）	投射極限/射影極限（projective limit）

本條目用語取歸納極限與射影極限。

定義

一範疇 C 中的極限及上極限可用 C 中的圖示來定義。形式上，C 中類型 J 的圖示是指一個由 J 映射至 C 的函子：

F : J → C.

範疇 J 稱之為「索引範疇」，圖示 F 可想做是以 J 索引 C 內的物件及態射。J 實際的物件及態射為何並不重要，關鍵在於之間的互動。

通常，最感興趣的情況是當類型J為小範疇或有限範疇之時，此類圖示分別被稱為「小圖示」及「有限圖示」。

極限

設 F : J → C 為一個在範疇 C 中類型 J 的圖示。一個對應於 F 的「錐體」是指 C 中的一物件 N ，具有可以 J 內之物件 X 索引的態射族 ψ_X : N → F(X)，使得對每個 J 內的態射 f : X → Y，均有 F(f) o ψ_X = ψ_Y。

圖示 F : J → C 的極限是一個對應於 F 的錐體 (L, φ)，使得對所有其他對應於 F 之錐體 (N, ψ)，總存在一個「唯一的」態射 u : N → L，使得對所有 J 中的 X，φ_X o u = ψ_X。

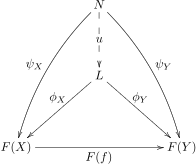A universal cone

可以說，錐體 (N, ψ) 能被唯一的因子 u 分解成錐體 (L, φ)。此一態射 u 有時稱為「中介態射」。

極限亦稱之為「泛錐體」，因為其所具有之泛性質（詳見下文）。如同每個泛性質一般，上述定義敘述了一個有關一般性的對稱狀態：極限物件 L 夠一般，能讓所有其他錐體分解；另一方面，L 也必須夠特殊，每個錐體都只可能有「一個」因子。

極限也可視為是在對應於 F 的錐體範疇內的終對象。

圖示可能不存在極限；但若一個圖示存在極限，則此一極限一定是唯一的：在同構下是唯一的。

上極限

極限及錐體的對偶概念是上極限及上錐體。雖然可直接將上述定義的所有態射反轉，以得到上極限及上錐體之定義，但下文仍將明確敘明之：

圖示 F : J → C 的「上錐體是指 C 中的一物件 N，具有可以每個 J 中的物件 X 索引的態射族

ψ_X : F(X) → N

使得對每個 J 內的態射 f : X → Y，均有 ψ_Y o F(f)= ψ_X。

圖示 F : J → C 的上極限是 F 的上錐體 (L, $\phi$)，使得對所有其他對應於 F 的上錐體 (N, ψ)，總存在一個「唯一的」態射 u : L → N，使得對所有 J 中的 X，u o $\phi$_X = ψ_X。

A universal co-cone

上極限也稱為「泛上錐體」，也可視為是在對應於 F 的上錐體範疇內的始對象。

如同極限一般，若圖示 F 存在上極限，則此上極限在同構下是唯一的。

歸納系統與射影系統

以下固定一個範疇${\mathcal {C}}$，並探討其中的極限。為避免集合的悖論，我們將固定一個宇宙${\mathcal {U}}$，並假定${\mathcal {C}}$是${\mathcal {U}}$-範疇，即：對任意兩個對象$X,Y$，態射集$\mathrm {Hom} _{\mathcal {C}}(X,Y)$同構於${\mathcal {U}}$裡的某個集合。$\mathbf {Set}$表所有${\mathcal {U}}$裡的集合構成的範疇。

設$I$為對${\mathcal {U}}$的一個小範疇，所謂歸納系統（或稱I-圖）係指一個函子$\alpha :I\rightarrow {\mathcal {C}}$，射影系統則指一函子$\beta :I^{\mathrm {op} }\rightarrow {\mathcal {C}}$。

形象地說，歸納系統不外是給定${\mathcal {C}}$中一族對象$\{X_{i}:i\in I\}$，對每個態射$i\rightarrow j$都有${\mathcal {C}}$中對應的態射$X_{i}\rightarrow X_{j}$，且此對應在態射的合成下不變。射影系統對應的態射則反向：$X_{i}\leftarrow X_{j}$。

固定一對象$X\in {\mathcal {C}}$，對任意歸納系統α或射影系統β，可定義從$I^{\mathrm {op} }$到$\mathbf {Set}$的函子

$\mathrm {Hom} _{\mathcal {C}}(\alpha ,X):i\mapsto \mathrm {Hom} (\alpha (i),X)$

$\mathrm {Hom} _{\mathcal {C}}(X,\beta ):i\mapsto \mathrm {Hom} (X,\beta (i))$

我們將遵循可表函子的哲學，從集合的射影極限出發。暫設${\mathcal {C}}=\mathbf {Set}$，$\mathbf {Set}$上的歸納系統不外是$I$上的預層。給定一個歸納系統β，定義：

$\varprojlim \beta :=\{(x_{i})\in \prod _{i\in I}\beta (i):\forall i,j\in I,s\in \mathrm {Hom} (i,j)\;\beta (s)(x_{j})=x_{i}\}$

（注意：若$I$是空範疇，對應的射影極限是單元素集合。）

可手工驗證下述自然同構：

$\mathrm {Hom} _{\mathbf {Set} }(X,\varprojlim \beta ){\stackrel {\sim }{\rightarrow }}\varprojlim \mathrm {Hom} _{\mathbf {Set} }(X,\beta )$

若干例子

始對象與終對象

令$I$為空範疇，此時的歸納極限與射影極限（若存在）便分別滿足泛性質

$\forall X\in {\mathcal {C}},|\mathrm {Hom} (X,\varprojlim \emptyset )|=|\mathrm {Hom} (\varinjlim \emptyset ,X)|=1$

這不外就是${\mathcal {C}}$裡的始對象與終對象。

纖維積與纖維餘積

令$I$為離散範疇（即：其間只有恆等態射），此時歸納及射影系統不外只是一族${\mathcal {C}}$的對象$\{X_{i}:i\in I\}$，對應的歸納極限及射影極限稱作餘積（又稱上積）與積。

令$I$為範疇$\bullet \longleftarrow \bullet \longrightarrow \bullet$；設$\alpha :I\rightarrow {\mathcal {C}}$對應於$Y_{1}{\stackrel {f_{1}}{\longleftarrow }}X{\stackrel {f_{2}}{\longrightarrow }}Y_{2}$。若其歸納極限存在，稱之$Y_{1},Y_{2}$對$X$的纖維餘積，寫作$Y_{1}\sqcup _{X}Y_{2}$。

對偶地看，對於$\beta :I^{\mathrm {op} }\rightarrow {\mathcal {C}}$，對應於$X_{1}{\stackrel {f_{1}}{\longrightarrow }}Y{\stackrel {f_{2}}{\longleftarrow }}X_{2}$，若其射影極限存在，稱之$X_{1},X_{2}$對$Y$的纖維積，寫作$X_{1}\times _{Y}X_{2}$。

纖維積與纖維餘積可視為「相對」版本的積與餘積。若存在終對象（或始對象），則積（或餘積）可視為對該對象的纖維積（或纖維餘積）。

核與上核

核（kernel）與餘核（cokernel，又譯上核），有時也稱等化子（equalizer）與餘等化子（coequalizer）。考慮對應到 $X_{0}{\overset {f}{\underset {g}{\rightrightarrows }}}X_{1}$ 的歸納或射影系統，此時的歸納極限$\mathrm {Coker} (f,g)$稱作上核，射影極限$\mathrm {Ker} (f,g)$稱作核。它們的泛性質圖解如下：

在加法範疇中僅須考慮$g=0$的狀況，上述概念遂歸結為同調代數所探討的核與餘核。

性質

極限之交換

設$I,J$為小範疇，$\alpha :I\times J\rightarrow {\mathcal {C}}$為歸納系統，則有自然同構

$\varinjlim _{i,j}\alpha (i,j)=\varinjlim _{i}\varinjlim _{j}\alpha (i,j)=\varinjlim _{j}\varinjlim _{i}\alpha (i,j)$

將箭頭反向，對射影系統$\beta :(I\times J)^{\mathrm {op} }=I^{\mathrm {op} }\times J^{\mathrm {op} }\rightarrow {\mathcal {C}}$亦有自然同構

$\varprojlim _{i,j}\beta (i,j)=\varprojlim _{i}\varprojlim _{j}\beta (i,j)=\varprojlim _{j}\varprojlim _{i}\beta (i,j)$

歸納極限與射影極限通常不交換，一個格外有用的結果是：若$I$是濾通範疇，則$\varinjlim _{I}$與任意$\varprojlim _{J}$交換。

完備性

若一個範疇內存在任意的（小）射影極限，則稱之完備範疇；完備的充要條件是存在任意的積與核。

將箭頭反向，遂得到上完備範疇的定義及其充要條件。

正合函子

更多信息：正合函子

考慮一個函子$F:{\mathcal {C}}\rightarrow {\mathcal {C'}}$。

• 若${\mathcal {C}}$裡存在任意的有限射影極限，且$F$與有限射影極限交換，則稱$F$為左正合。
• 若${\mathcal {C}}$裡存在任意的有限歸納極限，且$F$與有限歸納極限交換，則稱$F$為右正合。
• 若上述條件同時被滿足，則稱$F$為正合。

在阿貝爾範疇中，上述定義回歸到同調代數中的定義。

根據極限的泛性質，$\mathrm {Hom} (-,-)$函子無論對哪個變數都是左正合的。

設$(F,G)$是一對伴隨函子。若${\mathcal {C}}$存在任意有限歸納極限，則$F$右正合；若存在任意有限射影極限，$G$左正合。此法可建立許多函子的正合性。

具體實例

集合論

• 定義中已構造集合的（小）射影極限。對於任意一個小範疇$I$及歸納系統$\alpha :I\rightarrow \mathbf {Set}$，其歸納極限亦存在，定義為下述商集：

$\varinjlim \alpha :={\dfrac {\coprod _{i\in I}\alpha (i)}{(\exists i_{1}\rightarrow \cdots \rightarrow i_{n},x\in \alpha (i_{1})\mapsto \cdots \mapsto y\in \alpha (i_{n}))\Rightarrow (x\sim y)}}$

• 兩個集合的纖維積與上積為

$Y_{1}\sqcup _{X}Y_{2}=Y_{1}\sqcup Y_{2}/\{f_{1}(y_{1})=f_{2}(y_{2})\Rightarrow x_{1}\sim x_{2}~\}$

$X_{1}\times _{Y}X_{2}=\{(x_{1},x_{2})\in X_{1}\times X_{2}:f(x_{1})=f(x_{2})\}$

• 設$f,g:X_{0}\rightarrow X_{1}$，則

$\mathrm {Ker} (f,g)=\{x_{0}\in X_{0}:f(x_{0})=g(x_{0})\}$，這是「等化」一詞的來由。

$\mathrm {Coker} (f,g)=X_{1}/\{\forall x_{0}\in X_{0},f(x_{0})\sim g(x_{0})\}$

• $\mathbf {Set}$是完備且上完備的。

拓撲空間

拓撲空間範疇$\mathbf {Top}$也是完備且上完備的。各種極限構造與集合相同，惟須安上適合的商拓撲或子空間的誘導拓撲。

特別是可以構造一族無窮多個拓撲空間的極限及逆極限，此時相應的拓撲稱作始拓撲或終拓撲。此類構造在泛函分析及同倫理論中特別有用。

一個拓撲空間$X$滿足豪斯多夫性質的充要條件是$p_{1},p_{2}:X\times X\rightarrow X$的核$\Delta :X\rightarrow X\times X$是閉浸入，將此性質推廣到概形上，則得到分離概形。

概形

概形範疇$\mathbf {Sch}$（或相對版本$\mathbf {Sch} _{/S}$）有終對象$\mathrm {Spec} \mathbb {Z}$（或$S$），並存在有限的纖維積。

抽象代數

阿貝爾群範疇$\mathbf {Ab}$或一個環$R$上的模範疇$\mathbf {Mod} _{R}$都是完備且上完備的。函子的正合性對應到交換代數裡的正合性概念。

射影極限的一個典型例子是p進整數：$\mathbb {Z} _{p}:=\varprojlim _{n}\mathbb {Z} /p^{n}\mathbb {Z}$。

文獻

• Masaki Kashiwara and Pierre Schapira, Categories and Sheaves, Springer. ISBN 3540279490

外部連結

• Categories, sites, sheaves and stacks /Pierre Schapira