
此條目介紹的是英文為Convex function的函數。關於英文為Concave function的函數,請見「
凹函數」。
 凸函數的圖像上任取兩點,連成的線段必在圖像上方。
凸函數的圖像上任取兩點,連成的線段必在圖像上方。
 二元二次多項式函數
二元二次多項式函數 的圖像,形如開口向上的碗。
的圖像,形如開口向上的碗。
凸函數(英文:Convex function)是指函數圖形上,任意兩點連成的線段,皆位於圖形的上方的實值函數,[1]如單變數的二次函數和指數函數。二階可導的一元函數 為凸,若且唯若其定義域為凸集,且函數的二階導數
為凸,若且唯若其定義域為凸集,且函數的二階導數 在整個定義域上非負。直觀理解,凸函數的圖像形如開口向上的杯
在整個定義域上非負。直觀理解,凸函數的圖像形如開口向上的杯 ,而相反,凹函數則形如開口向下的帽
,而相反,凹函數則形如開口向下的帽 。
。
在最優化研究中,凸函數的最小化問題有唯一性,即凸開集上的嚴格凸函數,至多只有一個極小值。
概率論中,凸函數 作用在某隨機變量期望值
作用在某隨機變量期望值![{\displaystyle \mathbb {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09de7acbba84104ff260708b6e9b8bae32c3fafa) 所得的結果,總不大於對隨機變量先取函數值再取期望,即
所得的結果,總不大於對隨機變量先取函數值再取期望,即
![{\displaystyle f(\mathbb {E} [X])\leq \mathbb {E} [f(X)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fee18709fba0e49ef57d378c3299f5132d5c0b8c)
稱為延森不等式。該不等式可以推導出均值不等式及赫爾德不等式等結果。
- 注意:中國大陸數學界某些機構關於函數凹凸性定義和國外的定義是相反的。Convex Function在某些中國大陸的數學書中指凹函數。Concave Function指凸函數。但在中國大陸涉及經濟學的很多書中,凹凸性的提法和其他國家的提法是一致的,也就是和數學教材是反的。舉個例子,同濟大學高等數學教材對函數的凹凸性定義與本條目相反,本條目的凹凸性是指其上方圖是凹集或凸集,而同濟大學高等數學教材則是指其下方圖是凹集或凸集,兩者定義正好相反。
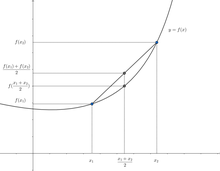
形像理解凸函數與延森不等式
 為某實向量空間的凸子集,若實值函數
為某實向量空間的凸子集,若實值函數 對任意
對任意  及任意
及任意 ,皆有
,皆有
![{\displaystyle f\left[v+t\cdot (w-v)\right]\leq f(v)+t\cdot \left[f(w)-f(v)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7520f1e626b4dd3241ef46e3682efe77e96e958)
則  稱為凸函數。
稱為凸函數。
若  ,然後在
,然後在  圖像上任取兩點
圖像上任取兩點 和
和 連線,則連線上某點
連線,則連線上某點  的
的  座標可以想成從
座標可以想成從  出發,前進了
出發,前進了  這整段的一部分而已,也就是說
這整段的一部分而已,也就是說

循着同樣的比例  ,
,  的
的  座標就可以寫成
座標就可以寫成

但同樣的  座標下,對應的
座標下,對應的  函數值就是
函數值就是
![{\displaystyle f\left[x_{1}+t\cdot (x_{2}-x_{1})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/253cae3e050107e5d778962098349a967103f6e8)
所以,凸函數的定義意為, 的圖像上,任意相異兩點的連線不能低於中間
的圖像上,任意相異兩點的連線不能低於中間 的曲線。[2]換言之,函數的上境圖(圖像上方的點的集合)為凸集。
的曲線。[2]換言之,函數的上境圖(圖像上方的點的集合)為凸集。
若將定義的 號換成
號換成 ,則得到嚴格凸的定義:
,則得到嚴格凸的定義:
 稱為嚴格凸,意思是對
稱為嚴格凸,意思是對 和任意不相等的
和任意不相等的 ,皆有
,皆有
![{\displaystyle f\left[v+t\cdot (w-v)\right]<f(v)+t\cdot \left[f(w)-f(v)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3edeb1d90faeff94b0fe50f431ea20606506ea1)
若  ,在嚴格凸函數
,在嚴格凸函數 的圖像曲線上,任意兩相異點的連線,除端點外皆高於曲線。
的圖像曲線上,任意兩相異點的連線,除端點外皆高於曲線。
若  ,實值函數
,實值函數 對於任意三實數
對於任意三實數  ,都有
,都有 ,則稱
,則稱  是幾乎凸的。
是幾乎凸的。
凸函數的某些性質,多元情況的敍述與一元情況同樣簡單。此種性質,可能僅於多元情況列舉,恕不在一元情況贅述。
 函數(藍色)是凸的,若且唯若其上方的區域(綠色)是一個凸集。
函數(藍色)是凸的,若且唯若其上方的區域(綠色)是一個凸集。
- 設
 是一元實函數,定義域為區間。考慮割線斜率
是一元實函數,定義域為區間。考慮割線斜率 則函數
則函數 是對稱函數,即關於
是對稱函數,即關於 。
。 為凸,當且僅當對每個固定的
為凸,當且僅當對每個固定的 ,皆有
,皆有 關於
關於 單調不減(或由對稱性,可將此句中
單調不減(或由對稱性,可將此句中 互換)。此刻劃有助證明以下的結果。
互換)。此刻劃有助證明以下的結果。
- 若一元凸函數
 定義在開區間
定義在開區間 內,則在C內連續,且處處有左側及右側的單邊導數。如此定義的兩個單邊導函數,皆為單調不減。由此推出,除可數個點外,
內,則在C內連續,且處處有左側及右側的單邊導數。如此定義的兩個單邊導函數,皆為單調不減。由此推出,除可數個點外, 在其他點皆可微(不過不可導的點組成的集合,仍有可能稠密)。如果
在其他點皆可微(不過不可導的點組成的集合,仍有可能稠密)。如果 是閉區間,那麼
是閉區間,那麼 有可能在
有可能在 的端點不連續,見例子。
的端點不連續,見例子。
- 一元可微函數在區間上是凸的,若且唯若函數位於所有它的切線的上方:[3]:69對於區間內的所有
 和
和 ,都有
,都有 特別地,如果
特別地,如果 ,則上式化為
,則上式化為 ,故
,故 是
是 的最小值。
的最小值。
- 一元可微函數在某個區間上是凸的,若且唯若它的導數在該區間上單調不減。若一元函數既凸又可導,則其導數也連續。
- 一元二階可微的函數在區間上是凸的,若且唯若它的二階導數是非負的;這是判斷某個函數是否凸的實用方法。直觀地,二階可導的凸函數「向上彎」,而不會屈向另一邊(即無拐點)。如果它的二階導數是正數,那麼函數就是嚴格凸的,但反過來不成立。例如,
 的二階導數是
的二階導數是 ,當
,當 時為零,但
時為零,但 是嚴格凸的。
是嚴格凸的。
- 此性質的條件「二階導數非負」與前一個性質的條件「導數單調不減」有差異。若
 在區間
在區間 非負,則的確
非負,則的確 在
在 單調不減。反之則不然,因為可能有
單調不減。反之則不然,因為可能有 在
在 單調不減,但在某點不可導,即
單調不減,但在某點不可導,即 在
在 中某點無定義。
中某點無定義。
- 若
 為一元凸函數,且
為一元凸函數,且 ,則
,則 在正數集內為超可加函數,即
在正數集內為超可加函數,即 對任意正實數
對任意正實數 成立。
成立。
更一般地,多元二次可微的連續函數在凸集上是凸的,若且唯若它的黑塞矩陣在凸集的內部是半正定的。
凸函數的任何極小值也是最小值。嚴格凸函數最多有一個最小值。
對於凸函數f,水平子集{x | f(x) < a}和{x | f(x) ≤ a}(a ∈ R)是凸集。然而,水平子集是凸集的函數不一定是凸函數;這樣的函數稱為擬凸函數。
延森不等式對於每一個凸函數f都成立。如果 是一個隨機變量,在f的定義域內取值,那麼
是一個隨機變量,在f的定義域內取值,那麼![{\displaystyle f(\mathbb {E} [X])\leq \mathbb {E} [f(X)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fee18709fba0e49ef57d378c3299f5132d5c0b8c) (在這裏,
(在這裏, 表示數學期望。)
表示數學期望。)
- 如果
 和
和 是凸函數,那麼
是凸函數,那麼 和
和 也是凸函數。
也是凸函數。
- 如果
 和
和 是凸函數,且
是凸函數,且 遞增,那麼
遞增,那麼 是凸函數。
是凸函數。
- 凸性在仿射映射下不變:也就是說,如果
 是凸函數(
是凸函數( ),那麼
),那麼 也是凸函數,其中
也是凸函數,其中
- 如果
 在
在 內是凸函數,且
內是凸函數,且 是一個凸的非空集,那麼
是一個凸的非空集,那麼 在
在 內是凸函數,只要對於某個
內是凸函數,只要對於某個 ,有
,有 。
。
- 函數
 處處有
處處有 ,因此f是一個(嚴格的)凸函數。
,因此f是一個(嚴格的)凸函數。
- 絕對值函數
 是凸函數,雖然它在點x = 0沒有導數。
是凸函數,雖然它在點x = 0沒有導數。
- 當
 時,函數
時,函數 是凸函數。
是凸函數。
- 定義域為[0,1]的函數f,定義為f(0)=f(1)=1,當0<x<1時f(x)=0,是凸函數;它在開區間(0,1)內連續,但在0和1不連續。
- 函數
 的二階導數為
的二階導數為 ,因此它在x ≥ 0的集合上是凸函數,在x ≤ 0的集合上是凹函數。
,因此它在x ≥ 0的集合上是凸函數,在x ≤ 0的集合上是凹函數。
- 每一個在
 內取值的線性變換都是凸函數,但不是嚴格凸函數,因為如果f是線性函數,那麼
內取值的線性變換都是凸函數,但不是嚴格凸函數,因為如果f是線性函數,那麼 。如果將「凸」替換為「凹」,該命題也成立。
。如果將「凸」替換為「凹」,該命題也成立。
- 每一個在
 內取值的仿射變換,也就是說,每一個形如
內取值的仿射變換,也就是說,每一個形如 的函數,既是凸函數又是凹函數。
的函數,既是凸函數又是凹函數。
- 每一個範數都是凸函數,這是由於三角不等式。
- 如果
 是凸函數,那麼當
是凸函數,那麼當 時,
時, 是凸函數。
是凸函數。
 和
和 為單調遞增但非凸的函數。
為單調遞增但非凸的函數。- 函數f(x) = 1/x2,f(0)=+∞,在區間(0,+∞)內是凸函數,在區間(-∞,0)內也是凸函數,但是在區間(-∞,+∞)內不是凸函數,這是由於x = 0處的奇點。
- Moon, Todd. Tutorial: Convexity and Jensen's inequality. [2008-09-04]. (原始內容存檔於2008-04-20).
- Rockafellar, R. T. Convex analysis. Princeton: Princeton University Press. 1970.
- Luenberger, David. Linear and Nonlinear Programming. Addison-Wesley. 1984.
- Luenberger, David. Optimization by Vector Space Methods. Wiley & Sons. 1969.
- Bertsekas, Dimitri. Convex Analysis and Optimization. Athena Scientific. 2003.
- Thomson, Brian. Symmetric Properties of Real Functions. CRC Press. 1994.
- Hiriart-Urruty, Jean-Baptiste, and Lemaréchal, Claude. (2004). Fundamentals of Convex analysis. Berlin: Springer.
- Krasnosel'skii M.A., Rutickii Ya.B. Convex Functions and Orlicz Spaces. Groningen: P.Noordhoff Ltd. 1961.
- Borwein, Jonathan, and Lewis, Adrian. (2000). Convex Analysis and Nonlinear Optimization. Springer.









![{\displaystyle \mathbb {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09de7acbba84104ff260708b6e9b8bae32c3fafa)
![{\displaystyle f(\mathbb {E} [X])\leq \mathbb {E} [f(X)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fee18709fba0e49ef57d378c3299f5132d5c0b8c)




![{\displaystyle f\left[v+t\cdot (w-v)\right]\leq f(v)+t\cdot \left[f(w)-f(v)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7520f1e626b4dd3241ef46e3682efe77e96e958)











![{\displaystyle f\left[x_{1}+t\cdot (x_{2}-x_{1})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/253cae3e050107e5d778962098349a967103f6e8)



![{\displaystyle f\left[v+t\cdot (w-v)\right]<f(v)+t\cdot \left[f(w)-f(v)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3edeb1d90faeff94b0fe50f431ea20606506ea1)














































