圖 1 )長球面坐標系的幾個坐標曲面 。紅色長球面的
μ
=
1
{\displaystyle \mu =1}
ν
=
45
∘
{\displaystyle \nu =45^{\circ }}
ϕ
=
−
60
∘
{\displaystyle \phi =-60^{\circ }}
二面角 角度是
|
ϕ
|
{\displaystyle \left|\phi \right|}
直角坐標 大約為
(
0.831
,
−
1.439
,
2.182
)
{\displaystyle (0.831,\ -1.439,\ 2.182)}
圖 2 )兩個焦點在 z-軸的橢圓坐標系繪圖。橫軸是 x-軸,豎軸是 z-軸。紅色橢圓(
μ
{\displaystyle \mu }
μ
{\displaystyle \mu }
x
>
0
{\displaystyle x>0}
ν
{\displaystyle \nu }
ν
{\displaystyle \nu }
長球面坐標系 (英語:Prolate spheroidal coordinates )是一種三維正交坐標系 。設定二維橢圓坐標系 包含於 xz-平面;兩個焦點
F
1
{\displaystyle F_{1}}
F
2
{\displaystyle F_{2}}
直角坐標 分別為
(
0
,
0
,
−
a
)
{\displaystyle (0,\ 0,\ -a)}
(
0
,
0
,
a
)
{\displaystyle (0,\ 0,\ a)}
扁球面坐標系 。)橢圓坐標系的兩個焦點,包含於 z-軸。長球面坐標系可以被視為橢球坐標系 的極限案例,其兩個最短的半軸的長度相同。
在三維空間裏,一個點 P 的長球面坐標
(
μ
,
ν
,
ϕ
)
{\displaystyle (\mu ,\ \nu ,\ \phi )}
x
=
a
sinh
μ
sin
ν
cos
ϕ
{\displaystyle x=a\ \sinh \mu \ \sin \nu \ \cos \phi }
y
=
a
sinh
μ
sin
ν
sin
ϕ
{\displaystyle y=a\ \sinh \mu \ \sin \nu \ \sin \phi }
z
=
a
cosh
μ
cos
ν
{\displaystyle z=a\ \cosh \mu \ \cos \nu }
其中,
μ
≥
0
{\displaystyle \mu \geq 0}
0
≤
ν
≤
π
{\displaystyle 0\leq \nu \leq \pi }
0
≤
ϕ
≤
2
π
{\displaystyle 0\leq \phi \leq 2\pi }
μ
{\displaystyle \mu }
坐標曲面 是長球面 :
z
2
a
2
cosh
2
μ
+
x
2
+
y
2
a
2
sinh
2
μ
=
cos
2
ν
+
sin
2
ν
=
1
{\displaystyle {\frac {z^{2}}{a^{2}\cosh ^{2}\mu }}+{\frac {x^{2}+y^{2}}{a^{2}\sinh ^{2}\mu }}=\cos ^{2}\nu +\sin ^{2}\nu =1}
每一個長球面都是由橢圓繞着 z-軸旋轉形成的。橢球面與 xz-平面的相交,是一個橢圓。沿着 x-軸,橢圓的短半軸長度為
a
sinh
μ
{\displaystyle a\sinh \mu }
a
cosh
μ
{\displaystyle a\cosh \mu }
±
a
{\displaystyle \pm a}
ν
{\displaystyle \nu }
旋轉雙葉雙曲面 :
z
2
a
2
cos
2
ν
−
x
2
+
y
2
a
2
sin
2
ν
=
cosh
2
μ
−
sinh
2
μ
=
1
{\displaystyle {\frac {z^{2}}{a^{2}\cos ^{2}\nu }}-{\frac {x^{2}+y^{2}}{a^{2}\sin ^{2}\nu }}=\cosh ^{2}\mu -\sinh ^{2}\mu =1}
當
ν
<
π
/
2
{\displaystyle \nu <\pi /2}
ν
>
π
/
2
{\displaystyle \nu >\pi /2}
ϕ
{\displaystyle \phi }
x
sin
ϕ
−
y
cos
ϕ
=
0
{\displaystyle x\sin \phi -y\cos \phi =0}
長球面坐標
μ
{\displaystyle \mu }
ν
{\displaystyle \nu }
h
μ
=
h
ν
=
a
sinh
2
μ
+
sin
2
ν
{\displaystyle h_{\mu }=h_{\nu }=a{\sqrt {\sinh ^{2}\mu +\sin ^{2}\nu }}}
方位角
ϕ
{\displaystyle \phi }
h
ϕ
=
a
sinh
μ
sin
ν
{\displaystyle h_{\phi }=a\sinh \mu \ \sin \nu }
無窮小體積元素是
d
V
=
a
3
sinh
μ
sin
ν
(
sinh
2
μ
+
sin
2
ν
)
d
μ
d
ν
d
ϕ
{\displaystyle dV=a^{3}\sinh \mu \ \sin \nu \ \left(\sinh ^{2}\mu +\sin ^{2}\nu \right)d\mu d\nu d\phi }
拉普拉斯算子 是
∇
2
Φ
=
1
a
2
(
sinh
2
μ
+
sin
2
ν
)
[
∂
2
Φ
∂
μ
2
+
∂
2
Φ
∂
ν
2
+
coth
μ
∂
Φ
∂
μ
+
cot
ν
∂
Φ
∂
ν
]
+
1
a
2
sinh
2
μ
sin
2
ν
∂
2
Φ
∂
ϕ
2
{\displaystyle \nabla ^{2}\Phi ={\frac {1}{a^{2}\left(\sinh ^{2}\mu +\sin ^{2}\nu \right)}}\left[{\frac {\partial ^{2}\Phi }{\partial \mu ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \nu ^{2}}}+\coth \mu {\frac {\partial \Phi }{\partial \mu }}+\cot \nu {\frac {\partial \Phi }{\partial \nu }}\right]+{\frac {1}{a^{2}\sinh ^{2}\mu \sin ^{2}\nu }}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}}
其它微分算子,像
∇
⋅
F
{\displaystyle \nabla \cdot \mathbf {F} }
∇
×
F
{\displaystyle \nabla \times \mathbf {F} }
(
μ
,
ν
,
ϕ
)
{\displaystyle (\mu ,\ \nu ,\ \phi )}
正交坐標系 條目內對應的一般公式。
當邊界條件涉及長球面 時,長球面坐標時常可以用來解析偏微分方程式 。例如,位置分別在 z-軸兩個焦點的電子,會產生怎樣的靜電場 ?一個關於氫離子
H
2
+
{\displaystyle H_{2}^{+}}
原子核 中間時,一個電子 的波函數 是什麼?另外一個很實際的問題是,兩個小電極尖端之間的電場是什麼?極限案例包括一根電線段 (
μ
=
0
{\displaystyle \mu =0}
ν
=
0
{\displaystyle \nu =0}
圖 3 )第二種長球面坐標系
(
σ
,
τ
,
ϕ
)
{\displaystyle (\sigma ,\ \tau ,\ \phi )}
坐標曲面 。紅色長球面的
σ
=
1.54
{\displaystyle \sigma =1.54}
τ
=
0.71
{\displaystyle \tau =0.71}
ϕ
=
−
60
∘
{\displaystyle \phi =-60^{\circ }}
二面角 角度是
|
ϕ
|
{\displaystyle \left|\phi \right|}
直角坐標 大約為
(
0.831
,
−
1.439
,
2.182
)
{\displaystyle (0.831,\ -1.439,\ 2.182)}
另外,還有一種比較有幾何直覺性的扁球面坐標系
(
σ
,
τ
,
ϕ
)
{\displaystyle (\sigma ,\ \tau ,\ \phi )}
σ
=
cosh
μ
{\displaystyle \sigma =\cosh \mu }
τ
=
cos
ν
{\displaystyle \tau =\cos \nu }
ϕ
=
ϕ
{\displaystyle \phi =\phi }
其中,
σ
≥
1
{\displaystyle \sigma \geq 1}
1
≥
τ
≥
−
1
{\displaystyle 1\geq \tau \geq -1}
0
≤
ϕ
≤
2
π
{\displaystyle 0\leq \phi \leq 2\pi }
與扁球面坐標系 不同,長球面坐標系並沒有簡併 。在三維空間裏,長球面坐標系與直角坐標 有一一對應 關係:
x
=
a
(
σ
2
−
1
)
(
1
−
τ
2
)
cos
ϕ
{\displaystyle x=a{\sqrt {\left(\sigma ^{2}-1\right)\left(1-\tau ^{2}\right)}}\cos \phi }
y
=
a
(
σ
2
−
1
)
(
1
−
τ
2
)
sin
ϕ
{\displaystyle y=a{\sqrt {\left(\sigma ^{2}-1\right)\left(1-\tau ^{2}\right)}}\sin \phi }
z
=
a
σ
τ
{\displaystyle z=a\ \sigma \ \tau }
σ
{\displaystyle \sigma }
坐標曲面 是長球面 :
z
2
a
2
σ
2
+
x
2
+
y
2
a
2
(
σ
2
−
1
)
=
1
{\displaystyle {\frac {z^{2}}{a^{2}\sigma ^{2}}}+{\frac {x^{2}+y^{2}}{a^{2}(\sigma ^{2}-1)}}=1}
每一個長球面都是由橢圓繞着 z-軸旋轉形成的。橢球面與 xz-平面的相交,是一個橢圓。沿着 x-軸,橢圓的短半軸長度為
a
σ
2
−
1
{\displaystyle a{\sqrt {\sigma ^{2}-1}}}
a
σ
{\displaystyle a\sigma }
±
a
{\displaystyle \pm a}
τ
{\displaystyle \tau }
旋轉雙曲面 :
z
2
a
2
τ
2
−
x
2
+
y
2
a
2
(
1
−
τ
2
)
=
1
{\displaystyle {\frac {z^{2}}{a^{2}\tau ^{2}}}-{\frac {x^{2}+y^{2}}{a^{2}(1-\tau ^{2})}}=1}
當
τ
>
0
{\displaystyle \tau >0}
τ
<
0
{\displaystyle \tau <0}
ϕ
{\displaystyle \phi }
x
sin
ϕ
−
y
cos
ϕ
=
0
{\displaystyle x\sin \phi -y\cos \phi =0}
任何一點 P 與焦點
F
1
{\displaystyle F_{1}}
F
2
{\displaystyle F_{2}}
d
1
{\displaystyle d_{1}}
d
2
{\displaystyle d_{2}}
d
1
+
d
2
=
2
a
σ
{\displaystyle d_{1}+d_{2}=2a\sigma }
d
1
−
d
2
=
2
a
τ
{\displaystyle d_{1}-d_{2}=2a\tau }
所以,點 P 與焦點
F
1
{\displaystyle F_{1}}
d
1
{\displaystyle d_{1}}
a
(
σ
+
τ
)
{\displaystyle a(\sigma +\tau )}
F
2
{\displaystyle F_{2}}
d
2
{\displaystyle d_{2}}
a
(
σ
−
τ
)
{\displaystyle a(\sigma -\tau )}
F
1
{\displaystyle F_{1}}
F
2
{\displaystyle F_{2}}
z
=
−
a
{\displaystyle z=-a}
z
=
+
a
{\displaystyle z=+a}
第二種長球面坐標
(
σ
,
τ
,
ϕ
)
{\displaystyle (\sigma ,\ \tau ,\ \phi )}
h
σ
=
a
σ
2
−
τ
2
σ
2
−
1
{\displaystyle h_{\sigma }=a{\sqrt {\frac {\sigma ^{2}-\tau ^{2}}{\sigma ^{2}-1}}}}
h
τ
=
a
σ
2
−
τ
2
1
−
τ
2
{\displaystyle h_{\tau }=a{\sqrt {\frac {\sigma ^{2}-\tau ^{2}}{1-\tau ^{2}}}}}
h
ϕ
=
a
(
σ
2
−
1
)
(
1
−
τ
2
)
{\displaystyle h_{\phi }=a{\sqrt {\left(\sigma ^{2}-1\right)\left(1-\tau ^{2}\right)}}}
無窮小體積元素是
d
V
=
a
3
(
σ
2
−
τ
2
)
d
σ
d
τ
d
ϕ
{\displaystyle dV=a^{3}\left(\sigma ^{2}-\tau ^{2}\right)d\sigma d\tau d\phi }
拉普拉斯算子 是
∇
2
Φ
=
1
a
2
(
σ
2
−
τ
2
)
{
∂
∂
σ
[
(
σ
2
−
1
)
∂
Φ
∂
σ
]
+
∂
∂
τ
[
(
1
−
τ
2
)
∂
Φ
∂
τ
]
}
+
1
a
2
(
σ
2
−
1
)
(
1
−
τ
2
)
∂
2
Φ
∂
ϕ
2
{\displaystyle \nabla ^{2}\Phi ={\frac {1}{a^{2}\left(\sigma ^{2}-\tau ^{2}\right)}}\left\{{\frac {\partial }{\partial \sigma }}\left[\left(\sigma ^{2}-1\right){\frac {\partial \Phi }{\partial \sigma }}\right]+{\frac {\partial }{\partial \tau }}\left[\left(1-\tau ^{2}\right){\frac {\partial \Phi }{\partial \tau }}\right]\right\}+{\frac {1}{a^{2}\left(\sigma ^{2}-1\right)\left(1-\tau ^{2}\right)}}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}}
其它微分算子,像
∇
⋅
F
{\displaystyle \nabla \cdot \mathbf {F} }
∇
×
F
{\displaystyle \nabla \times \mathbf {F} }
(
μ
,
ν
,
ϕ
)
{\displaystyle (\mu ,\ \nu ,\ \phi )}
正交坐標系 條目內對應的一般公式。
如同球坐標 解答的形式為球諧函數 ,拉普拉斯方程 可以用分離變數法 來求解,得到形式為長扁球諧函數 的答案。假若,邊界條件涉及長球面,我們可以優先選擇這方法來解析。
Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 661.
ξ
1
=
a
cosh
μ
{\displaystyle \xi _{1}=a\cosh \mu }
ξ
2
=
sin
ν
{\displaystyle \xi _{2}=\sin \nu }
ξ
3
=
cos
ϕ
{\displaystyle \xi _{3}=\cos \phi }
Zwillinger D. Handbook of Integration. Boston, MA: Jones and Bartlett. 1992: p. 114. ISBN 0-86720-293-9
u
k
{\displaystyle u_{k}}
ξ
k
{\displaystyle \xi _{k}}
Smythe, WR. Static and Dynamic Electricity 3rd ed. New York: McGraw-Hill. 1968. Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 97.
ξ
=
cosh
μ
{\displaystyle \xi =\cosh \mu }
η
=
sin
ν
{\displaystyle \eta =\sin \nu }
ϕ
=
ϕ
{\displaystyle \phi =\phi }
Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 177.
(
μ
,
ν
,
ϕ
)
{\displaystyle (\mu ,\ \nu ,\ \phi )}
(
σ
,
τ
,
ϕ
)
{\displaystyle (\sigma ,\ \tau ,\ \phi )}
Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: p. 180–182. 餘緯度
θ
=
90
∘
−
ν
{\displaystyle \theta =90^{\circ }-\nu }
緯度
ν
{\displaystyle \nu }
Moon PH, Spencer DE. Oblate spheroidal coordinates (η, θ, ψ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer Verlag. 1988: pp. 28–30 (Table 1.06). ISBN 0-387-02732-7
θ
=
90
∘
−
ν
{\displaystyle \theta =90^{\circ }-\nu }
ϕ
{\displaystyle \phi }
ψ
{\displaystyle \psi }
Landau LD, Lifshitz EM, Pitaevskii LP. Electrodynamics of Continuous Media (Volume 8 of the Course of Theoretical Physics) 2nd edition. New York: Pergamon Press. 1984: pp. 19–29. ISBN 978-0750626347 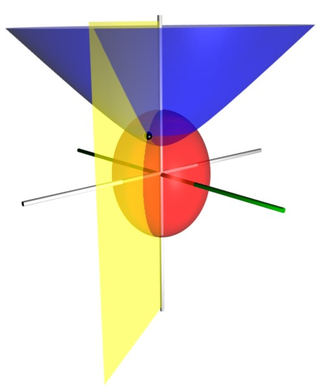


































![{\displaystyle \nabla ^{2}\Phi ={\frac {1}{a^{2}\left(\sinh ^{2}\mu +\sin ^{2}\nu \right)}}\left[{\frac {\partial ^{2}\Phi }{\partial \mu ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \nu ^{2}}}+\coth \mu {\frac {\partial \Phi }{\partial \mu }}+\cot \nu {\frac {\partial \Phi }{\partial \nu }}\right]+{\frac {1}{a^{2}\sinh ^{2}\mu \sin ^{2}\nu }}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48caeab189e1f1d9da9233fb21d53bb92851f8fc)




































![{\displaystyle \nabla ^{2}\Phi ={\frac {1}{a^{2}\left(\sigma ^{2}-\tau ^{2}\right)}}\left\{{\frac {\partial }{\partial \sigma }}\left[\left(\sigma ^{2}-1\right){\frac {\partial \Phi }{\partial \sigma }}\right]+{\frac {\partial }{\partial \tau }}\left[\left(1-\tau ^{2}\right){\frac {\partial \Phi }{\partial \tau }}\right]\right\}+{\frac {1}{a^{2}\left(\sigma ^{2}-1\right)\left(1-\tau ^{2}\right)}}{\frac {\partial ^{2}\Phi }{\partial \phi ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f15e727f9d0e40ee12fa68cb58a07f2011f82707)








